
Pro koncept identifikace jednotky číslici, musíme se nejprve seznámit s pojmem cykličnost. Cyklicita libovolného čísla je o poslední číslici a o tom, jak se objevují určitým definovaným způsobem. Vezměme si příklad, abychom tuto věc vyčistili:
graf cyklicity 2 je:
21 =2
22 =4
23 =8
24=16
25=32
podívejte se na výše uvedené. Viděli byste, že jak se 2 násobí pokaždé svým vlastním já, poslední číslice se změní. Při 4. násobení má 25 stejnou jednotkovou číslici jako 21. To nám ukazuje, že cyklicita 2 je 4, to znamená, že po každém čtvrtém násobení bude jednotková číslice dvě.
Cyklus tabulce:
cyklus tabulka pro čísla je uvedena níže:
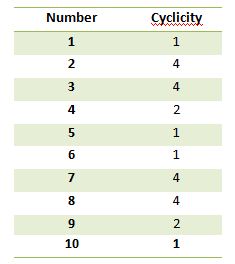
Jak jsme se zjistit, výše uvedené? Množte se a přesvědčte se sami. Je to dobrá praxe.
nyní použijeme koncept cyklicity pro výpočet jednotkové číslice čísla.
jaká je jednotková číslice výrazu 4993?
Teď máme dva způsoby, jak vyřešit to, ale jsme vybrat si nejlepší způsob, jak to vyřešit tj. přes cyklus
víme, že cyklus 4 je 2
podívejte se:
41 =4
42 =16
43 =64
44 =256
Z výše uvedeného je zřejmé, že cyklus 4 je 2. Nyní se cyklus číslo, tj. s 2 rozdělit dána moc, tj. 993 o 2, co bude zbytek, zbytek bude 1, takže odpověď až 4 umocněné jeden je 4.Jednotková číslice je v tomto případě 4.
Pro kontrolu, zda jste se naučili téma, myslím, že nějaké číslo, jako je toto, vypočítat jeho jednotky číslici a potom zkontrolujte si to s pomocí kalkulačky.
Poznámka : Pokud je zbytek nulový, v každém případě pak jednotka číslice bude poslední číslice acyclicity číslo
kde a je dané číslo a cykličnost číslo je uvedeno na výše uvedeném obrázku.
umožňuje vyřešit další příklad:
číslice v jednotkovém místě čísla 7295 X 3158 je
a. 7
B. 2
C. 6
D. 4
Řešení
Cyklus stůl pro 7 je následující:
71 =7
72 =49
73 = 343
74 = 2401
Pojďme rozdělit 295 4 a zbytek je 3.
poslední číslice 7295 se tedy rovná poslední číslici 73, tj. 3.
Cyklus stůl pro 3 je následující:
31 =3
32 =9
33 = 27
34 = 81
35 = 243
Pojďme rozdělit 158 4, zbytek je 2. Poslední číslice tedy bude 9.
proto číslice jednotky (7925 X 3158) je číslice jednotky součinu číslice na místě jednotky 7925 a 3158 = 3 * 9 = 27. Odpověď je tedy možnost 1.
