Pravděpodobně nejvíce široce používané hodnoty v půdě zpráva je půda únosnosti. Zřejmým důvodem je, že základní příklady uvedené ve většině učebnic téměř vždy používají únosnost k výpočtu rozměru plánu základu. Vzhledem k jednoduchosti a snadnosti použití je tato metoda stále základním parametrem půdy pro návrh základů. Tato jednoduchost však předpokládá, že se základna bude chovat jako tuhé tělo. Tento konkrétní předpoklad funguje dobře v praxi pro malé a jednotlivé sloupce patky. Ale u velkých a více sloupcových základů většina inženýrů preferuje flexibilní analýzu. Ruční výpočet flexibilní analýzy by mohl být náročný a téměř ve všech případech i softwarové programy jako STAAD, SAFE, GT STRUDL atd. jsou používány. Tyto počítačové programy však často požadují vstup nazvaný „modul reakce podkladu“. Mnoho inženýrů není s tímto pojmem obeznámeno a často se ho snaží porovnat s únosností. Vzhledem k tomu, že stále více inženýrů bude používat software k navrhování základů, je nezbytné, aby inženýři měli základní znalosti o tomto parametru půdy. Existuje nějaký vztah mezi únosností a modulem reakce podloží?
modul Subgrade reakce (Ks)
tento výraz se měří a vyjadřuje jako intenzita zatížení na jednotku výtlaku. Pro anglický jednotkový systém je často vyjádřen v kip / in2 / in; v systému SI je vyjádřen jako KN / m2 / m. Někteří vyjadřují tento termín v kip / in3 (nebo kN/m3), což může být zavádějící. Numericky je Kip / in3 správný, ale nepředstavuje správně fyzikální význam měřené hodnoty a může být zaměněn jako jednotka hustoty nebo objemové měření.
Matematicky, součinitel podloží reakce je vyjádřena jako:
Ks = p/s (Eqn 1)
, kde p = kontakt intenzita tlaku a s = půdní vypořádání
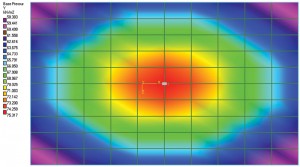
Obrázek 1a: Deformace obrázku a tlaku na půdu contour.
obrázek 1b: obrys tlaku půdy.
Jako Terzaghi bylo zmíněno, správný odhad kontaktní tlak pro flexibilní základ by mohl být velmi těžkopádné, takže se předpokládá, že Ks zůstává konstantní po celé úrovni. Jinými slovy, poměr mezi tlakem a vypořádáním na všech místech základny zůstane konstantní. Takže diagram posunutí základny se zátěží ve středu bude mít dishing efekt. Bod ve středu základny zažije nejvyšší posunutí. Posunutí se snižuje, když se pohybuje od středu. Obrázek 1a ukazuje jednoduchý základ desky na stupni. Byl modelován a analyzován v Nadaci STAAD jako „Mat“, což je flexibilní základ; půda byla definována pomocí koeficientu reakce podkladu. Pro toto cvičení byla použita výchozí hodnota softwaru pro modul reakce podkladu. Diagram posunutí ukazuje dishing efekt, jak bylo uvedeno výše. Obrázek 1b ukazuje obrys tlaku půdy. Je také zřejmé, že intenzita tlaku ve středu je maximální a snižuje se, jak se prvky (nebo souřadnice uzlu) pohybují od středu. Dalo by se tedy předpokládat, že poměr intenzity tlaku a osídlení je konstantní.
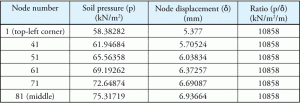
Tabulka 1: tlak půdy, posun uzlů a jejich poměr.
zvažte některá čísla ze stejného příkladu. Tlak půdy, odpovídající posunutí a poměr jsou uvedeny v tabulce 1. Body jsou zastoupeny na diagonále znázorňují kolísání tlaku a posunutí jako body pohybovat od středu k nejvzdálenějšímu bodu v rohu obdélníkový základ. Figura 2 ukazuje body na rohož desce.
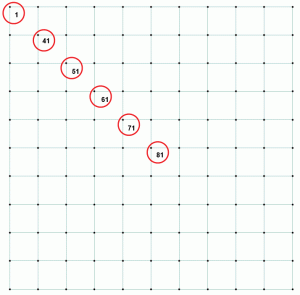
Obrázek 2: Vybrané body pro porovnání základního tlaku, průhybu a poměru.
to je stěží překvapení, protože modul reakce podkladu (Ks) je podle definice konstanta pro celý základ a program použil Ks jako svou půdní vlastnost. Je také důležité si uvědomit, že výchozí hodnota Ks softwaru (10858 KN / m2 / m) byla přesně stejná jako konstantní poměr vypočtený v tabulce 1.
základní tlak byl vypočítán z podpůrné reakce. Jeden by si mohl myslet, že poměr podpůrné reakce a odpovídajícího posunutí bude také konstantní. Jak je uvedeno v tabulce 2, poměry nejsou konstantní pro všechny hodnoty. Jak se hodnota Ks používá uvnitř programu a jak se vypočítá základní tlak?
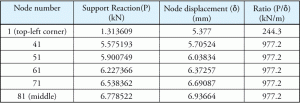
Tabulka 2: podpůrná reakce a posunutí.
Přítok Oblasti
Často předpoklad je, aby vypočítat, jak velkou plochu desky lze připsat na uzel nebo, jinými slovy, vliv každého uzlu na plochu desky. Záleží na tvaru desky. Pro dokonalou čtvercovou nebo obdélníkovou desku bude každý uzel ovlivňovat přesně ¼ plochy povrchu desky (obrázek 3a). Ale pro zobecněný čtyřúhelník by nejlepším postupem bylo vypočítat střed hmoty desky a poté nakreslit čáry z tohoto středu do středních bodů každé strany. Na obrázku 3b představuje stínovaná oblast vlivovou plochu odpovídajícího uzlu.
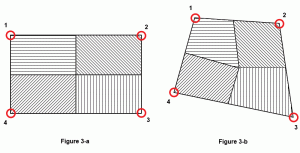
obrázek 3: oblast přítoků uzlu.
Podpora Pružina je Konstantní,
výše popsané přítok oblasti výpočtu je klíčové řízení interně používaný komerční software pro výpočet lineární pružiny konstantní. Program nejprve vypočítá přítok oblasti pro každý uzel základ a pak násobí modul reakce podloží odpovídající přítok oblasti pro každý uzel získat lineární pružiny konstantní v každém uzlu.
Ťij = Ks x Tai (Eqn 2)
, kde
Ťij je na jaře konstantní na i-tý uzel
Tai je vliv prostoru-tému uzlu
Ks je modul reakce podloží
Pro betonový základ analýzy těchto pramenů musí být definována jako komprese-pouze, jako je beton se předpokládá, že nebude provádět žádné tahové síly. Základní tlak se vypočítá v každém nosném uzlu dělením podpůrné reakce s odpovídající přítokovou oblastí uzlu. Pokud se podíváme na výše uvedený příklad, uzel 1 má mnohem menší přítokovou oblast než ostatní uzly. Lze také poznamenat, že všechny ostatní uzly mají stejnou přítok. To vysvětluje tabulku 2, protože ukazuje poměr pro uzel 1 se liší od ostatních uzlů. Obrázek 4 ukazuje přítokovou oblast pro různé uzly. Uzel 1 má přítok, který je 25% uzlu 81. Tabulka 3 je rozšíření tabulek 1 a 2 a ukazuje, jak je dosaženo konstantního poměru pro všechny uzly.
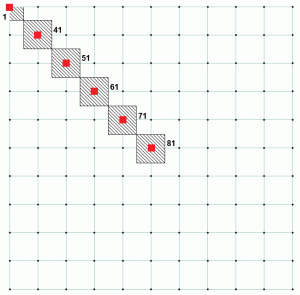
obrázek 4: Přítoková oblast vybraných uzlů.
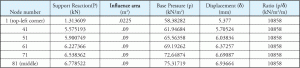
Tabulka 3: reakce, základní tlak, posunutí, Ks konstanta.
přípustné osídlení
únosnost je měření tlaku půdy, který může půda bezpečně nést. Jinými slovy, únosnost je tlak, který půda vydrží, než selže. Dvě nejdůležitější půdy selhání kritéria jsou:
- Smykové selhání
- Maximální přípustné vypořádání
Mezi mnoha faktory, nadace šířka (B) mohou ovlivnit kritéria selhání. Obvykle se střihové selhání řídí pro menší základy a selhání vypořádání řídí větší základy. Tabulka 4 je typickým příkladem, který ukazuje vztah mezi různými velikostmi základů a kritérii selhání.
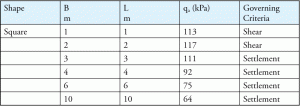
Tabulka 4: Final přípustnou únosnost pro přípustné vypořádání = 25 mm a vzhledem kotevní hloubka.
pro odhad selhání vypořádání se předpokládá přípustná hodnota vypořádání (obvykle 25 mm nebo 1 palec). Když se půda usadí více, než je přípustná hodnota, půda selže. Takže i pro výpočet únosnosti se používá přípustné osídlení půdy a stavební inženýři by si měli být vědomi této hodnoty při navrhování základny. Přípustná hodnota osídlení půdy je obvykle nedílnou součástí každé zprávy o půdě.
Proč Používat Modul Reakce Podloží
To bylo dříve uvedl, že k návrhu pružný mat foundation, modul reakce podloží se používá místo únosnosti půdy. Ale proč? Odpověď spočívá v základních předpokladech, jak by se nadace mohla chovat.
základy mohou být tuhé nebo pružné. Únosnost se používá k návrhu tuhých základů, ale pro flexibilní základy se používá reakce podkladu. Samotný předpoklad tuhého základu je, že “ rozložení reakce podloží p nad základnou základu musí být rovinné, protože tuhý základ zůstává rovinný, když se usadí.“Zvažte jednoduše podporovaný paprsek naložený v jeho středu, jak je znázorněno na obrázku 5a. statikou můžeme získat R1 = P / 2 a R2 = P/2. Kdyby stejný paprsek je načten excentricky, reakce lze vypočítat, jak je znázorněno na Obrázku 5b.
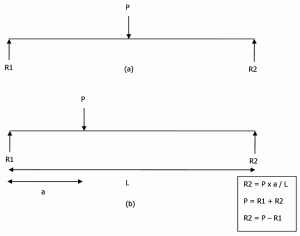
Obrázek 5: Reakce na jednoduše podporovaný paprsek.
stejný koncept je rozšířen pro konstrukci pevných základů. Ale místo koncových podpěr je podporován celý základ. Rovněž se předpokládá, že relativní tuhost betonové desky je mnohem vyšší než tuhost půdy. Předpokládá se tedy, že deska zůstane rovinná i po aplikaci zatížení.
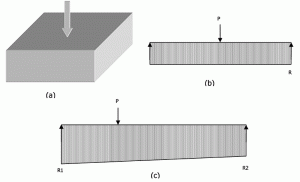
Obrázek 6: Dílčí třídy reakce na izolované postavení.
obrázek 6a ukazuje patku naloženou ve středu. Z analogie tuhého širokého paprsku, P = R x L. Podobně, pro excentricky naloženo postavení, reakce se bude měnit lineárně od jednoho konce na druhý, jak je znázorněno na Obrázku 6c. Rovnice 3 a 4 může být vyřešen najít konci reakce. Ale žádná z rovnic neobsahuje modul reakce podkladu (Ks). Takže „distribuce reakce podkladu na bázi tuhé základny je nezávislá na stupni stlačitelnosti podkladu“, na kterém spočívá. Jak mnozí autoři dospěli k závěru, pevný základ může být bezpečně navržen pomocí únosnosti, protože ve většině případů tato metoda přináší konzervativnější výsledky.
P = 1/2L(R1 + R2) (Eqn 3)
P x = 1/6B2R1 + 1/3B2R2 (Eqn 4)
Ale mat foundation je často navržen jako flexibilní základ, jak to může být velký ve velikosti, a tam může být mnoho zatížení body a další složitosti, včetně děr a třídy trámy. K tomuto trendu přispívá široká dostupnost softwaru FEA. Na rozdíl od tuhých základů však flexibilní základ nemůže mít lineární reakci podkladu. Spíše to závisí na stlačitelnosti základu a na konstrukční tuhosti. Flexibilní základ je vystaven vnitřnímu ohýbání a relativním posunům mezi dvěma deskovými body. Čím větší je konstrukční tuhost, tím menší je relativní posunutí. Autor testoval pouzdro s velmi vysokou tuhostí deskových prvků, což vedlo k téměř rovinnému povrchu po aplikaci zatížení. Podobně, čím větší je modul reakce podkladu, tím menší je rozložení tlaku. Jinými slovy, vyšší hodnota Ks absorbuje větší tlak v místě aplikace zatížení. Proto, modul reakce podloží, což je funkce půdy vyrovnání a vnější tlak,se používá pro flexibilní základové konstrukci.
Korelace
nejčastější a pravděpodobně nejbezpečnější – odpověď na otázku korelace mezi únosnosti a modul reakce podloží, je, že neexistuje žádná korelace. Měl by však existovat jeden, protože obě jsou měření kapacit půdy a kterýkoli z těchto dvou parametrů lze použít k návrhu pravidelného základu.
Opět platí, že definice Ks je tlak na jednotku vypořádání. Jinými slovy, schopnost půdy odolat tlaku pro daný posun. Z dřívějších diskusí je také zřejmé, že i únosnost má přípustné vypořádání. Je proto lákavé dospět k závěru, že modul reakce podloží je únosnost na jednotku osídlení.
tento závěr je velmi podobný rovnici předložené Bowlesem.
SI: Ks = 40(SF)qa kN/m3 (Eqn 5)
FPS: Ks = 12(SF)qa k/ft3 (Eqn 6)
kde SF = Bezpečnostní faktor a qa je přípustná nosnost.
v rovnicích 5 a 6 je přípustná únosnost nejprve převedena na konečnou únosnost vynásobením bezpečnostním faktorem. Autor předpokládal osadu jeden palec nebo 25 mm. Konečná rovnice je pak formulována dělením konečné únosnosti předpokládaným vypořádáním.
obecnější podobu rovnice lze zapsat jako:
Ks = 
napětí/přemístění (Eqn 7)
, kde
I = Bezpečnostní faktor
qa je přípustná nosnost
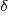je přípustné půdy vypořádání
Tyto rovnice jasně ukazují, že odpovídající bezpečnostní faktor musí být použit, a Ks hodnota může být lepší v porovnání s maximální nosností spíše než povolenou nosnost. Bezpečnostní faktor se může lišit v závislosti na projektech a geotechnických inženýrech. Dalším důležitým faktorem je předpokládané přípustné vypořádání vypočtené únosnosti.
Podobně, je třeba poznamenat, že základní hodnoty tlaku uvádí FEA analýzy nelze přímo srovnávat s nosností. Maximální základní tlak by měl být vynásoben bezpečnostním faktorem a poté porovnán s přípustnou únosností půdy.
nicméně výše uvedené rovnice mají omezení. Mohou být použity na patky, kde se řídí selhání vypořádání, ale nemohou být spojeny se patkami, kde dojde k selhání střihu před dosažením přípustného limitu vypořádání. Inženýři tedy musí před použitím těchto rovnic postupovat opatrně.
závěr
korelace mezi únosností a modulem reakce podloží je v nejlepším případě odhadem. Může být použit pro odhad, ale hodnota Ks určená zkouškou zatížení desky by měla být vždy použita, pokud je k dispozici, nebo by měla být požadována, kdykoli je to možné. Výše uvedená diskuse však poskytuje vhled do těchto hodnot a pomáhá inženýrům pochopit fyzický význam modulu reakce podkladu. A jako vždy, stavební inženýři by se měli před dokončením tuhosti půdy a hodnot ložisek poradit s odborníkem na geotechnický inženýr.▪