Hospodář Transformace
Hospodář Transformace (také „Hospodář Reflexe“) je ortogonální transformace reflexe:
- to reflex vektory ve sloupcích matice takové, že
- první vektor má všechny nuly až na první prvek
Transformační Matice
Odraz transformace:
Vlastnosti
Hospodář matice jsou symetrické a ortogonální: jsou odrazem matice
Odvození
Takže máme $P = I – 2vv^T$:
Budeme používat takové transformace pro nulování prvků
QR Rozklad
Jako v případě LU Rozkladu, kde jsme aplikovali sérii Gauss Transformační změny, můžeme udělat to samé, a provádět řadu Hospodář Transformace
- takže když jsme se vybrat $y = \pm e_1$ (kde $e_1$ je matice s 1 na pozici 1 a zbytek jsou nuly)
- pak to bude nula všechny prvky z $x$, kromě prvního
- tak vhodnou volbou $H$ můžeme vzít $A$ a nula, všechny sub-diagonální prvky
- můžete to udělat několikrát pro každý sloupec $A$
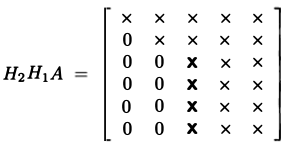
Tímto způsobem můžeme provést QR Rozklad:
Hessenberg Rozkladu
Namísto použití to pro reducting matice na Trojúhelníkový tvar, můžeme použít Hospodář Transformace snížit matice Matice Hessenberg