Redaktørens Note: Tony Abbey underviser i live NAFEMS FEA-klasser i USA, Europa og Asien. Han underviser også nafems e-learning klasser globalt. Kontakt .for detaljer.
en tidligere Desktop Engineering-artikel (“forenkle FEA-simuleringsmodeller ved hjælp af Plan symmetri”) forklarede, at selv med kraftfulde moderne computere er der ofte en motivation til at bruge forenklingsteknikker i strukturel endelig elementanalyse (FEA). Denne opfølgning beskriver, hvordan to nært beslægtede metoder kan bruges til at tage 2D-skiver gennem en kompleks struktur i regioner af interesse. De resulterende FEA-modeller kan give værdifuld indsigt i lokale belastninger hurtigere og mere effektivt end en fuld 3d-model. De fortæller ikke hele historien, men er værdifulde værktøjer til CAE-ingeniøren.
de to FEA-metoder kaldes planspænding og planstamme. Begge bruger 2D plane elementer, der ligner tynde skalelementer og er maskeret ved hjælp af Plan overfladegeometri.
Planspændingsanalyse
Fig. 1 viser de vigtige fakta om Plane stress analyse. Den strukturelle region antages at ligge i 2D-planet, med den tredje strukturelle dimension relativt lille. I figuren er dette tykkelsen i å-retningen. Der findes spændinger i 2D-planet som sigma, sigma y (direkte spændinger) og sigma y (forskydningsspænding i Plan). Hver af disse spændinger er konstant gennem tykkelsen som vist i indsatsen. Derudover kan der ikke være stress i å-retningen. Dette stress-stamme materialeforhold er defineret i 2D-planspændingselementer, der anvendes i denne type analyse.
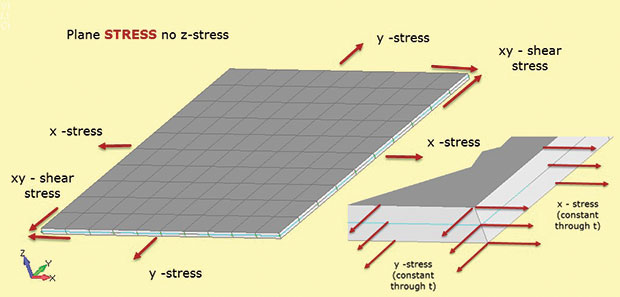Fig. 1: Plane stress; Stress tilstand antagelser.manglen på å-stress er måden at huske elementtypebetegnelsen planspænding (dvs.kun i planspændinger tilladt). Der er heller ingen gennemgående tykkelse forskydningsspændinger. Vi kunne indlæse planspændingsmodellen i Fig. 1 med en biaksial belastning og beregne Sigma og sigma y. der er ingen sigma å. vi kan også beregne de tilsvarende in-plane stammer e-H og e-y. hvis vi anvender en forskydningsbelastning, kan vi finde forskydningsspænding sigma og forskydningsstamme e-h. Dette er ikke nul, da modellen er fri til at tynde ned i å, da den strækker sig i H og y. der er ingen begrænsning uden for flyet for at forhindre dette. I nogle løsere kan vi genvinde den gennem tykkelsesstamme e-å og bruge den til at beregne ændringen i tykkelse. (Hvis modellen er i biaksial kompression, bliver å-sektionen tykkere). Dette betragtes normalt som en sekundær belastning og er muligvis ikke tilgængelig til output—men det er der og kan beregnes manuelt, hvis det er nødvendigt.
Fig. 2 viser en aluminium lug komponent. Lugen stikker ud fra et sammensat arklayup, der har lag placeret og bundet over tangs (eller ben) og underkropssektion. Tangs overfører belastningen på lugen til kompositstrukturen. I praksis vil lagene blive trappet for at muliggøre en jævn forskydningsoverførsel gennem bindingen til kompositmaterialet. Forskydningsoverførslen til kompositmaterialet simuleres her ved diffust overflade trækkraft kræfter “trækker” på tangs. Disse afbalancerer den påførte lugbelastning.
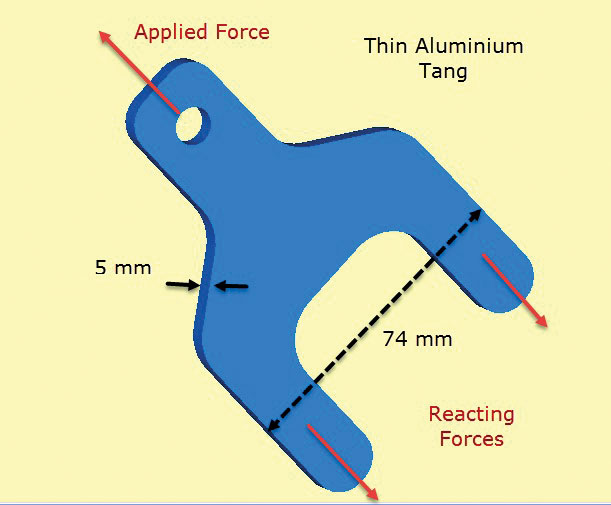Fig. 2: Tyndvægget aluminium tang overførsel belastning i komposit struktur.den vigtigste antagelse her er, at gennem tykkelsesspændinger er nul, og spændingerne i Plan er konstante gennem tykkelse i komponenten. Dette betyder, at den lokale detalje af forskydningsbelastningsoverførslen fra komposit til tang er dårligt modelleret. Men fokus for denne analyse er at kontrollere dimensionering af lug og tang tværsnit fri af den sammensatte, ved hjælp af In-plane spændinger.
komponentens tykkelse er lille sammenlignet med andre dimensioner. Denne værdi er input som den faktiske tykkelse i Planet stress element definition.
Fig. 3 viser FEA-modellen og de beregnede maksimale hovedstolspændinger. De områder af interesse er omkring lug og skulder radier. I den virkelige verden ville stresstilstanden ved spændingskoncentrationerne være 3D, og gennem tykkelse ville Sigma-spændinger og forskydningsspændinger balancere lokalt. Det er dog meget rimeligt her at antage, at spændingerne i flyet dominerer. Dette er den samme antagelse implicit i de fleste traditionelle stresskoncentrationsberegninger (Kt), der findes i håndbøger.
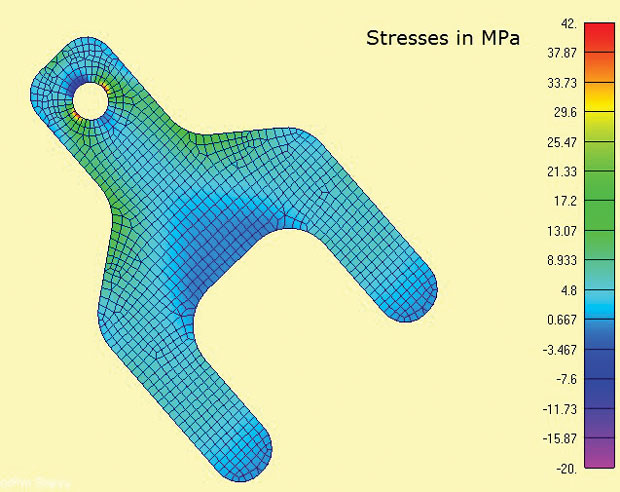Fig 3: 2D planspændingselementer, der viser maksimale hovedspændinger et af de praktiske træk ved planspændingsanalysen er, at det er en strengt 2D-analyse, så kun tre frihedsgrader (DOF) skal begrænses (in-plan oversættelser H, y og rotation omkring å-akse). Dette egner sig til 3-2-1 minimumsbegrænsningsmetoden med afbalanceret belastning. I et 2D-tilfælde degenererer dette til en 2-1-metode. En knude har DOF og y begrænset, en anden passende ortogonal knude har DOF begrænset. Dette gør det muligt at anvende reaktionsbelastningen i tangs direkte som diffuse afbalanceringsbelastninger. Det ville være vanskeligt at simulere denne grænsetilstand via begrænsninger til jorden.
den gennemgående tykkelse e-å stamme og dermed udtynding af tangs kunne beregnes som en sekundær effekt.
Planstamme Analyse
Fig. 4 viser essensen af planestammen metode. Igen bruges 2D plane elementer, men med subtilt forskellige antagelser. De in-plane spændinger er udviklet som før. Men denne gang er det out-of-plane, eller gennem tykkelse å stamme, som er indstillet til nul. Så planestamme analyse tillader kun stammer i Plan. Dette fungerer godt til at repræsentere tykke strukturer som vist. Tilstedeværelsen af dette meget materiale har en tendens til at stabilisere komponenten og forhindre, at den spændes i å. dette betyder også, at der udvikles konstante gennem tykkelsesspændinger i strukturen. Denne stress-stamme materialeforhold er defineret i 2D plane stamme elementer, der anvendes i denne type analyse.
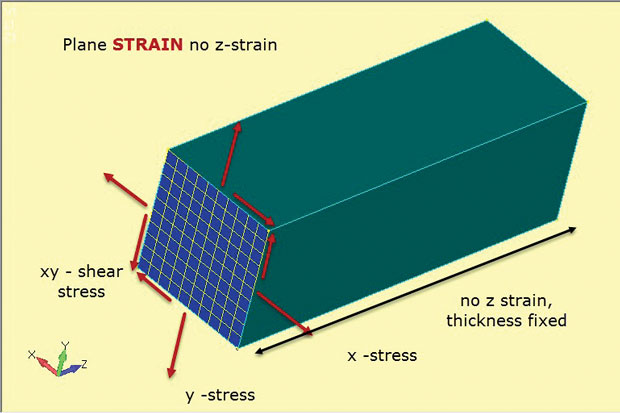Fig. 4: Plane stamme analyse; stress og stamme tilstand antagelser.figuren viser orienteringen af 2D-planestammen elementer som et snit sektion gennem en typisk dyb komponent. Antagelsen er, at spændingstilstanden ved dette snitsektion vil blive duplikeret ved enhver hhv.planskæring (å-station) gennem komponenten. Komponenten antages at være prismatisk (med et konstant tværsnit) ned i længden.
i praksis bruger vi denne metode, hvor stresstilstanden varierer langsomt fra Plan til plan i en dyb komponent. Der skal være nok materiale gennem dybden til at stabilisere og eliminere den gennemgående tykkelsestamme. Dette er det samme princip, der anvendes på brudsejhedsprøver vist i Fig. 5. En fejl under plane belastningsbetingelser er vist for midtersektionen af den tykke prøve. Fejlen ved de frie kanter og den tynde sektion er en anden tilstand, mere som en planspændingstilstand. Definition være en god repræsentation af midterlinjens tykke prøveopførsel, men ikke af de frie kanter eller den tynde prøve.
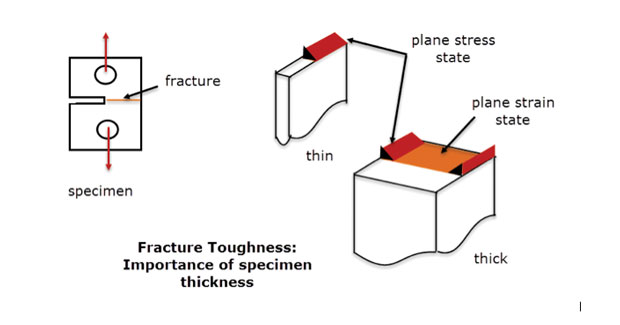Fig. 5: brud sejhed prøver; tynde og tykke sektioner.Fig. 6 viser en anden komponent anvendt i en sammensat struktur, der danner en bundet samling. Her er sektionen konstant og dyb nok, så vi kan antage, at spændingerne også er konstante med dybden. De frie endeflader (ved + å, – å) vil have en anden lokal stresstilstand (faktisk planspænding, som nævnt), men formålet med denne analyse er at kontrollere nettosektionsspændingerne på midterlinjen (å = 0).
2D-planstamme-analysenettet er vist inddelt i 3D-komponenten i Fig. 7. Snittet er defineret ved station å = 0.
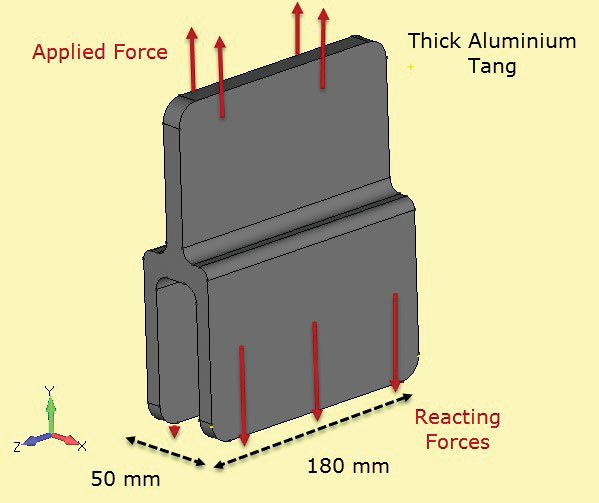Fig 6: dyb sektion aluminium tang.
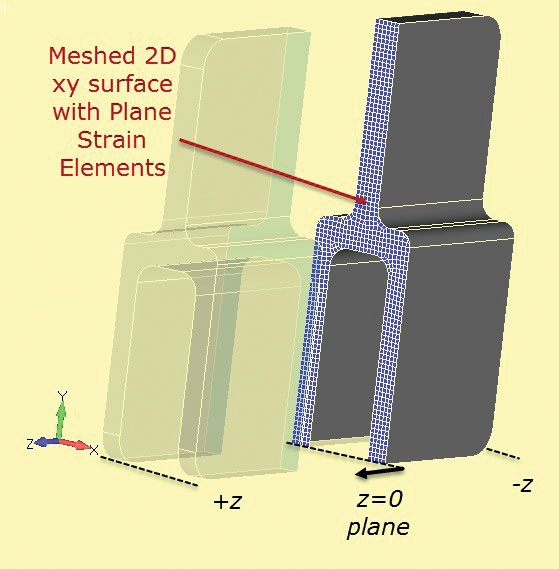Fig. 7: Sektion skåret gennem solid sektion for at udvikle 2D plan stamme sektion.der kan bruges et meget fint 2D-planstamme, som kører meget hurtigt sammenlignet med en fuld 3d-model. 2-1-begrænsningsmetoden bruges som før. Belastningen skal overvejes nøje. “Tykkelsen” af planestammen er ret vilkårlig og er normalt indstillet til 1,0 som standard. Hvis belastningen på komponenten beregnes som en løbende belastning gennem dybden (N/m, Lbf/inch osv.) så kan denne værdi bruges direkte på flyet strain mesh. Det er nyttigt at vælge et afsnit, såsom den enkelte tang og estimere den nominelle eller gennemsnitlige stress i dette afsnit for den fulde komponent. Dette kan bruges som en sanity check i plane strain analyse. Forkert indlæsning er sandsynligvis den vigtigste årsag til fejl i denne metode.
resultaterne af analysen er vist i Fig. 8 og vis tydeligt regionerne med høj stress omkring skulderfileten. Spændingerne gælder for komponentens centrale dybdeområde (å = 0).
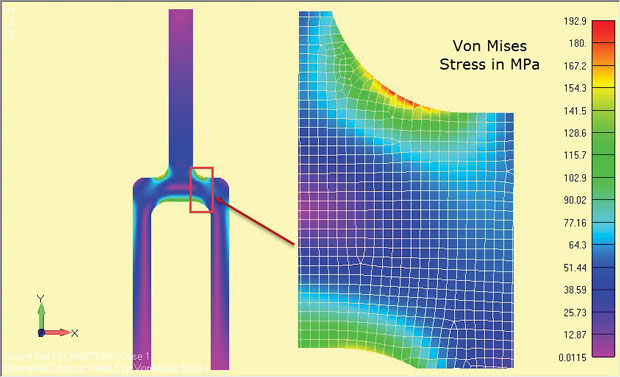Fig. 8: Plane stamme analyseresultater af en dyb tang komponent.de anvendte stressmængder afhænger af den anvendte solver. Nogle løsere ignorerer å-retningsspændingerne som sekundære og genvinder spændingerne i Planet. De vigtigste belastninger og von Mises-belastninger vedrører derefter en 2D-stresstilstand i Plan. Hvis spændingen i retningen genvindes, skal den identificeres tydeligt, så 2D-stresstilstanden i Planet kan identificeres.
hvad repræsenterer stress i retningen? Det er den stress, der er udviklet på grund af håndhævelsen af nul å retningsstamme. Spændingen virker som om de frie endeflader af den prismatiske sektion blev rettet. Ved det centrale plan for en dyb sektionskomponent vil disse være de komplementære spændinger, der er nødvendige for at holde nul-retningen belastningstilstand. I virkeligheden, når vi bevæger os mod de frie overfladeflader, falder spændingen til nul og bliver en plan spændingsfordeling (som det ses i den tykke brudmekanikprøve).
i mange tilfælde, såsom en trykcylinder, er endefladerne lukket og vil faktisk udvikle en aksial spænding på grund af aksiale kræfter. Dette vil være en anden stress end den inducerede aksiale stress i planestammen analyse. En håndberegning vil være nødvendig for at beregne de aksiale spændinger eller mulig en supplerende aksisymmetrisk model for trykbeholdere.
den lette geometri og maskekonstruktion egner sig godt til “hvad-hvis” – studier eller mere formelle formoptimeringsstudier.
til sammenligning blev en halv symmetri fuld 3D-analyse af den dybe tang-komponent udført, og resultaterne er vist i Fig. 9. Den nominelle spænding over det øverste enkelt tangben er identisk i begge tilfælde—husk, at dette er grundlaget for enhver sundhedskontrol.
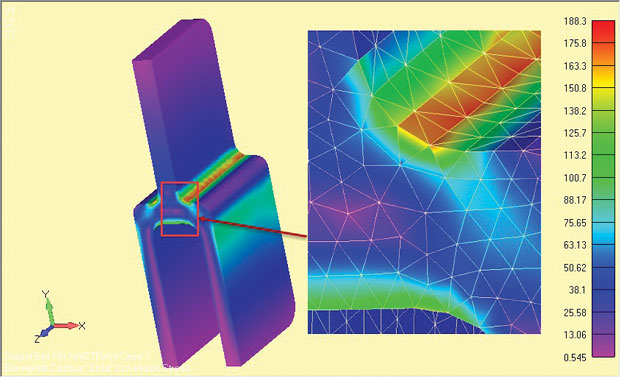Fig. 9: Fuld 3D-model af den dybe tang, der viser stressresultater.de lokale skulderspændinger er lavere med en lille procentdel i den fulde model. Dette er af tre grunde. For det første er det relativt Grove 3D tet-net ringere end det meget fine 2D-planstamme lokale net. Der er ikke foretaget en konvergenskontrol af 3D-modellen.
for det andet er der en lille ændring i geometri på de frie overflader (+å,- å) sammenlignet med å = 0 sektionen på grund af endefileterne. I dette tilfælde er effekten ubetydelig, da fileterne er væk fra skulderregionerne. I mange komponenter vil der dog være lokale fileter og løbe ud detaljer. hvilket vil variere geometrien fra et simpelt plan ansigt. Lokale stressvariationer ved frie endeflader skal muligvis estimeres eller kontrolleres med en fuld 3d-model.
endelig er antagelsen om planstamme af en fast å-begrænsning ved +å, – å-sektioner ikke sandt for en endelig dybdekomponent. Stress vil diffundere til nul ved de “rigtige” frie ansigter. Denne effekt er vist i Fig. 10, som bruger 3D-modellen som den er, og også som en simulering af flystammen.
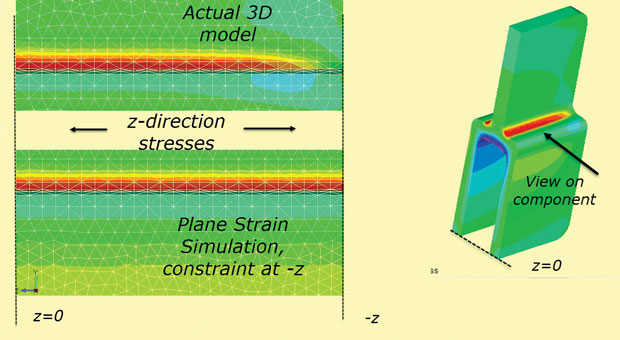Fig. 10: Diffusion af å-stress mod den frie overflade.hurtig og effektiv
planspændings-og planspændingsanalyser er nyttige 2D-metoder, der ofte kan supplere 3D-modeller i fuld skala. Ikke alle funktioner kan repræsenteres, men med en vis opfindsomhed kan stress på nøgleområder i det mindste estimeres. Motivationen for at bruge metoderne er at muliggøre hurtig effektiv analyse med nem 2D geometri og mesh konstruktion.