Lær OpenCV

i dette indlæg lærer vi detaljerne i histogrammet for orienterede gradienter (HOG) Funktionsbeskrivelse. Vi lærer, hvad der er under hætten, og hvordan denne deskriptor beregnes internt af OpenCV, MATLAB og andre pakker.

dette indlæg er en del af en serie, jeg skriver om billedgenkendelse og Objektdetektion.

den komplette liste over tutorials i denne serie er angivet nedenfor:

1. billedgenkendelse ved hjælp af traditionelle computervisionsteknikker : Del 1
2. Histogram af orienterede gradienter : Del 2
3. eksempelkode til billedgenkendelse : Del 3
4. træning af en bedre øjedetektor: del 4a
5. Objektdetektion ved hjælp af traditionelle computervisionsteknikker : del 4b
6. Sådan træner du og tester din egen OpenCV-objektdetektor : Del 5
7. billedgenkendelse ved hjælp af dyb læring : Del 6
   • Introduktion til neurale netværk
   • forståelse af fremadgående neurale netværk
   • billedgenkendelse ved hjælp af indviklede neurale netværk
8. Objektdetektion ved hjælp af dyb læring: Del 7

mange ting ser vanskelige og mystiske ud. Men når du tager dig tid til at dekonstruere dem, erstattes mysteriet med mestring, og det er det, vi er efter. Hvis du er nybegynder og finder computersyn hårdt og mystisk, skal du bare huske følgende

spørgsmål : Hvordan spiser du en elefant ?
A : En bid ad gangen!

Hvad er en funktionsbeskrivelse?

en feature deskriptor er en repræsentation af et billede eller et billede patch, der forenkler billedet ved at udtrække nyttige oplysninger og smide fremmede oplysninger.

typisk konverterer en funktionsbeskrivelse et billede af størrelsesbredde 3 (kanaler ) til en funktionsvektor / array af længde n. i tilfælde af HOG-funktionsbeskrivelsen er inputbilledet af størrelse 64 128 3, og outputfunktionsvektoren er af længde 3780.

Husk at HOG descriptor kan beregnes for andre størrelser, men i dette indlæg holder jeg mig til tal præsenteret i det originale papir, så du nemt kan forstå konceptet med et konkret eksempel.

alt dette lyder godt, men hvad er “nyttigt” og hvad er “fremmed” ? For at definere “nyttigt” skal vi vide, hvad er det “nyttigt” til ? Det er klart, at funktionsvektoren ikke er nyttig med det formål at se billedet. Men det er meget nyttigt til opgaver som billedgenkendelse og objektdetektering. Funktionsvektoren produceret af disse algoritmer, når den føres ind i en billedklassificeringsalgoritmer som Support Vector Machine (SVM) giver gode resultater.

men hvilke slags “funktioner” er nyttige til klassificeringsopgaver ? Lad os diskutere dette punkt ved hjælp af et eksempel. Antag, at vi vil bygge en objektdetektor, der registrerer knapper på skjorter og frakker.

en knap er cirkulær ( kan se elliptisk ud i et billede ) og har normalt et par huller til syning. Du kan køre en kantdetektor på billedet af en knap og nemt fortælle om det er en knap Ved blot at se på kantbilledet alene. I dette tilfælde er edge information “nyttig” og farve information er ikke. Derudover SKAL funktionerne også have diskriminerende magt. For eksempel skal gode funktioner, der udvindes fra et billede, være i stand til at fortælle forskellen mellem knapper og andre cirkulære genstande som mønter og bildæk.

i HOG-funktionsbeskrivelsen bruges fordelingen ( histogrammer ) af retninger af gradienter ( orienterede gradienter ) som funktioner. Gradienter af et billede er nyttige, fordi størrelsen af gradienter er stor omkring kanter og hjørner ( regioner med pludselige intensitetsændringer), og vi ved, at kanter og hjørner pakker meget mere information om objektform end flade områder.

Sådan beregnes Histogram af orienterede gradienter ?

i dette afsnit vil vi gå ind i detaljerne i beregningen af HOG feature deskriptor. For at illustrere hvert trin bruger vi en patch af et billede.

Trin 1 : Forbehandling

som nævnt tidligere HOG feature deskriptor anvendes til fodgænger detektion beregnes på en 64 till 128 patch af et billede. Selvfølgelig kan et billede være af enhver størrelse. Typisk patches på flere skalaer analyseres på mange billedsteder. Den eneste begrænsning er, at de patches, der analyseres, har et fast billedformat. I vores tilfælde skal patcherne have et billedformat på 1: 2. For eksempel kan de være 100 kr 200, 128 kr 256 eller 1000 kr 2000, men ikke 101 kr 205.

for at illustrere dette punkt, jeg har vist et stort billede af størrelse 720 til 475. Vi har valgt en patch af størrelse 100 liter 200 til beregning af vores HOG feature deskriptor. Denne patch er beskåret ud af et billede og skaleres til 64 venstre 128. Nu er vi klar til at beregne SVINEBESKRIVELSEN for denne billedpatch.

papiret fra Dalal og Triggs nævner også gammakorrektion som et forbehandlingstrin, men præstationsgevinsterne er mindre, og derfor springer vi over trinnet.

Trin 2: Beregn Gradientbillederne

for at beregne en HOG-deskriptor skal vi først beregne de vandrette og lodrette gradienter; vi vil trods alt beregne histogrammet af gradienter. Dette opnås let ved at filtrere billedet med følgende kerner.

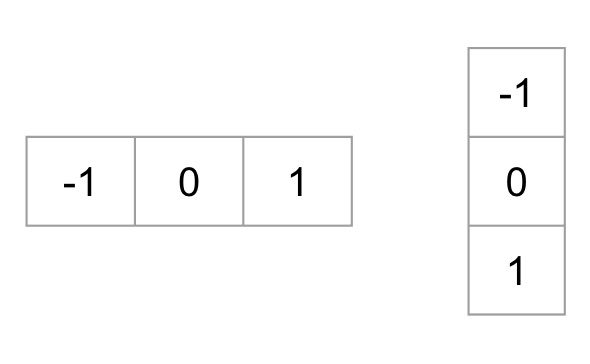
vi kan også opnå de samme resultater ved at bruge Sobel operator i OpenCV med kernestørrelse 1.

// C++ gradient calculation.// Read imageMat img = imread("bolt.png");img.convertTo(img, CV_32F, 1/255.0);// Calculate gradients gx, gyMat gx, gy;Sobel(img, gx, CV_32F, 1, 0, 1);Sobel(img, gy, CV_32F, 0, 1, 1);

# Python gradient calculation # Read imageim = cv2.imread('bolt.png')im = np.float32(im) / 255.0# Calculate gradientgx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)

dernæst kan vi finde størrelsen og retningen af gradienten ved hjælp af følgende formel

hvis du bruger OpenCV, kan beregningen udføres ved hjælp af funktionen cartToPolar som vist nedenfor.

// C++ Calculate gradient magnitude and direction (in degrees)Mat mag, angle;cartToPolar(gx, gy, mag, angle, 1);

den samme kode i python ser sådan ud.

# Python Calculate gradient magnitude and direction ( in degrees )mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

nedenstående figur viser gradienterne.

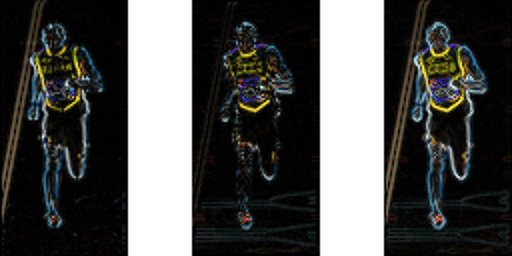
Bemærk, at gradienten skyder på lodrette linjer, og y-gradienten skyder på vandrette linjer. Størrelsen af gradientbrande, hvor der nogensinde er en skarp ændring i intensitet. Ingen af dem skyder, når regionen er glat. Jeg har bevidst udeladt billedet, der viser gradientretningen, fordi retning vist som et billede ikke formidler meget.

gradientbilledet fjernede en masse ikke-væsentlige oplysninger ( f.eks. Med andre ord kan du se på gradientbilledet og stadig let sige, at der er en person på billedet.

ved hvert punkt har gradienten En størrelse og en retning. For Farvebilleder evalueres gradienterne for de tre kanaler ( som vist i figuren ovenfor ). Størrelsen af gradienten ved et punkt er det maksimale af størrelsen af gradienter af de tre kanaler, og vinklen er den vinkel, der svarer til den maksimale gradient.

Trin 3: Beregn Histogram af gradienter i 8 liter 8 celler

i dette trin er billedet opdelt i 8 liter 8 celler, og et histogram af gradienter beregnes for hver 8 liter 8 celler.

vi vil lære om histogrammerne om et øjeblik, men inden vi går derhen, lad os først forstå, hvorfor vi har opdelt billedet i 8 liter 8 celler. En af de vigtige grunde til at bruge en funktionsbeskrivelse til at beskrive en patch af et billede er, at det giver en kompakt repræsentation. En 8-8-billedpatch indeholder 8h8h3 = 192 billedværdier. Gradienten af denne patch indeholder 2 værdier (størrelse og retning ) pr.

i slutningen af dette afsnit vil vi se, hvordan disse 128 numre er repræsenteret ved hjælp af et 9-bin histogram, der kan gemmes som et array på 9 numre. Ikke alene er repræsentationen mere kompakt, beregning af et histogram over en patch gør denne repræsentation mere robust over for støj. Individuelle graidenter kan have støj, men et histogram over 8 liter 8 patch gør repræsentationen meget mindre følsom over for støj.

men hvorfor 8 til 8 lappe ? Hvorfor ikke 32 Det 32 ? Det er et designvalg informeret af omfanget af funktioner, vi leder efter. HOG blev oprindeligt brugt til fodgængerdetektion. 8 liter 8 celler i et foto af en fodgænger skaleret til 64 liter 128 er store nok til at fange interessante funktioner ( f.eks. ).

histogrammet er i det væsentlige en vektor ( eller et array ) på 9 bakker (tal ) svarende til vinkler 0, 20, 40, 60 … 160.

lad os se på en 8-liters 8-patch på billedet og se, hvordan gradienterne ser ud.

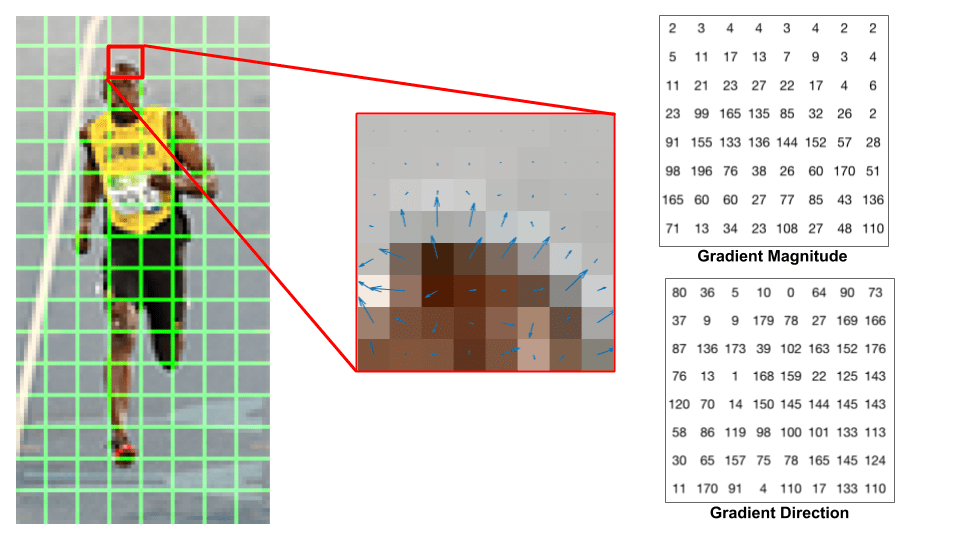
hvis du er nybegynder i computersyn, er billedet i midten meget informativt. Det viser lappen på billedet overlejret med pile, der viser gradienten — pilen viser gradientens retning, og dens længde viser størrelsen. Bemærk, hvordan pilens retning peger på retningen for ændring i intensitet, og størrelsen viser, hvor stor forskellen er.

til højre ser vi de rå tal, der repræsenterer gradienterne i de 8 liter 8 celler med en mindre forskel — vinklerne er mellem 0 og 180 grader i stedet for 0 til 360 grader. Disse kaldes” usignerede ” gradienter, fordi en gradient og den er negativ er repræsenteret af de samme tal. Med andre ord betragtes en gradientpil og den ene 180 grader modsat den som den samme. Men hvorfor ikke bruge 0-360 grader ?

empirisk har det vist sig, at usignerede gradienter fungerer bedre end underskrevne gradienter til fodgængerdetektion. Nogle implementeringer af HOG giver dig mulighed for at angive, om du vil bruge underskrevne gradienter.

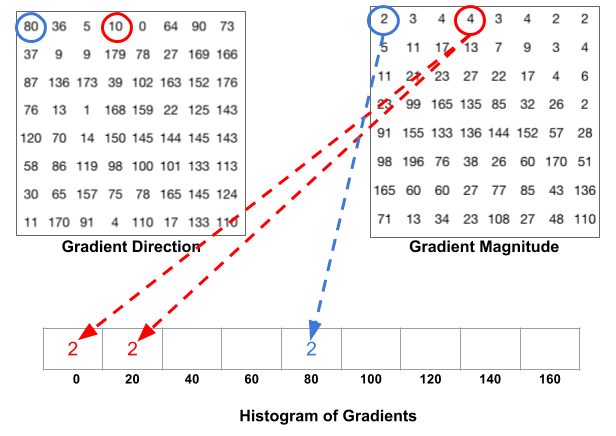
det næste trin er at oprette et histogram af gradienter i disse 8 liter 8 celler. Histogrammet indeholder 9 kasser svarende til vinkler 0, 20, 40 … 160. Følgende figur illustrerer processen. Vi ser på størrelsen og retningen af gradienten af den samme 8 prist 8 patch som i den foregående figur.

en bin vælges ud fra retningen, og afstemningen ( den værdi, der går ind i bin ) vælges ud fra størrelsen. Lad os først fokusere på billedet omgivet af blåt. Den har en vinkel (retning ) på 80 grader og en størrelse på 2. Så det tilføjer 2 til 5.bin. Gradienten ved billedpunktet omkranset ved hjælp af rødt har en vinkel på 10 grader og en størrelse på 4. Da 10 grader er halvvejs mellem 0 og 20, deles afstemningen jævnt i de to skraldespande.

der er endnu en detalje at være opmærksom på. Hvis vinklen er større end 160 grader, er den mellem 160 og 180, og vi ved, at vinklen vikles rundt, hvilket gør 0 og 180 ækvivalente. Så i eksemplet nedenfor bidrager billedpunktet med Vinkel 165 grader proportionalt til 0 graders bin og 160 graders bin.

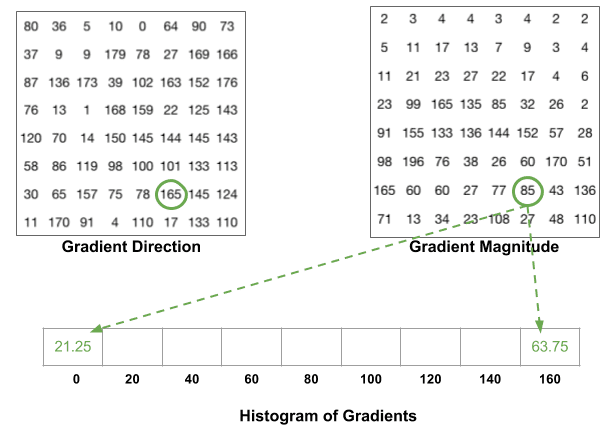
bidragene fra alle billedpunkterne i 8-kar-8-cellerne tilføjes for at oprette 9-bin histogrammet. For plasteret ovenfor ser det sådan ud

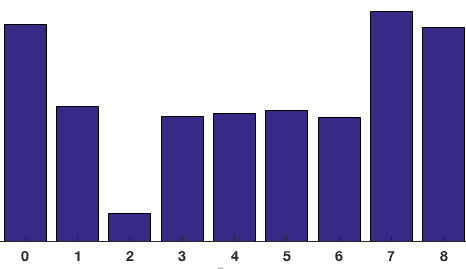
i vores repræsentation er y-aksen 0 grader. Du kan se histogrammet har en masse vægt nær 0 og 180 grader, hvilket er bare en anden måde at sige, at i patch gradienter peger enten op eller ned.

Trin 4 : 16 16 blok normalisering

i det foregående trin oprettede vi et histogram baseret på billedets gradient. Gradienter af et billede er følsomme over for den samlede belysning. Hvis du gør billedet mørkere ved at dividere alle billedværdier med 2, ændres gradientstørrelsen med halvdelen, og derfor ændres histogramværdierne med halvdelen.

ideelt set ønsker vi, at vores deskriptor skal være uafhængig af lysvariationer. Med andre ord vil vi gerne “normalisere” histogrammet, så de ikke påvirkes af lysvariationer.

før jeg forklarer, hvordan histogrammet normaliseres, lad os se, hvordan en vektor af længde 3 normaliseres.

lad os sige, at vi har en RGB-farvevektor . Længden af denne vektor er ${128^2 + 64^2 + 32^2} = 146.64$. Dette kaldes også vektorens L2-norm. At dele hvert element i denne vektor med 146,64 giver os en normaliseret vektor .

overvej nu en anden vektor, hvor elementerne er to gange værdien af den første vektor 2h = . Du kan selv finde ud af , at normalisering vil resultere i, hvilket er det samme som den normaliserede version af den originale RGB-vektor. Du kan se, at normalisering af en vektor fjerner skalaen.

nu hvor vi ved, hvordan man normaliserer en vektor, kan du blive fristet til at tro, at mens du beregner HOG, kan du simpelthen normalisere 9-kar-1-histogrammet på samme måde som vi normaliserede 3-kar-1-vektoren ovenfor. Det er ikke en dårlig ide, men en bedre ide er at normalisere over en større størrelse blok af 16 til 16.

en 16-liters 16-blok har 4 histogrammer, der kan sammenkædes til dannelse af en 36-1-elementvektor, og den kan normaliseres, ligesom en 3-liters 1-vektor normaliseres. Vinduet flyttes derefter med 8 billedpunkter (se animation), og en normaliseret 36-liters 1-vektor beregnes over dette vindue, og processen gentages.

Trin 5 : Beregn HOG-funktionsvektoren

for at beregne den endelige funktionsvektor for hele billedpatchen sammenkædes de 36 prit 1-vektorer til en kæmpe vektor. Hvad er størrelsen af denne vektor ? Lad os beregne

1. hvor mange positioner af de 16 liter 16 blokke har vi ? Der er 7 vandrette og 15 lodrette positioner, hvilket gør i alt 7 gange 15 = 105 positioner.
2. hver 16-lyste 16-blok er repræsenteret af en 36-lyste 1-vektor. Så når vi sammenkæder dem alle til en gaint-vektor, får vi en 36-liters 105 = 3780-dimensionel vektor.

visualisering af Histogram af orienterede gradienter

SVINEDESKRIPTOREN for et billedplaster visualiseres normalt ved at plotte de 9 liter 1 normaliserede histogrammer i 8 liter 8 celler. Se billede på siden. Du vil bemærke, at dominerende retning af histogrammet fanger personens form, især omkring torso og ben.

Desværre er der ingen nem måde at visualisere SVINEBESKRIVELSEN i OpenCV.

Abonner & Hent Kode