jeg er begyndt at gøre andres populære machine learning kursus på Coursera. Den første uge dækker meget, i det mindste for en person, der ikke har rørt meget beregning i et par år
- Omkostningsfunktioner (gennemsnitlig forskel kvadreret)
- Gradient Descent
- lineær Regression
disse tre emner var meget at tage ind. Jeg vil tale om hver i detaljer, og hvordan de alle passer sammen, med nogle python kode til at demonstrere.
Rediger 4. maj: Jeg offentliggjorde en opfølgning med fokus på, hvordan Omkostningsfunktionen fungerer her, herunder en intuition, hvordan man beregner den manuelt og to forskellige Python-implementeringer. Jeg kan gøre gradient nedstigning og derefter bringe dem sammen til lineær regression snart.
Modelrepræsentation
først er målet med de fleste maskinlæringsalgoritmer at konstruere en model: en hypotese, der kan bruges til at estimere Y baseret på H. hypotesen eller modellen kortlægger input til output. Så for eksempel sige, at jeg træner en model baseret på en masse boligdata, der inkluderer husets størrelse og salgsprisen. Ved at træne en model kan jeg give dig et skøn over, hvor meget du kan sælge dit hus til baseret på dets størrelse. Dette er et eksempel på et regressionsproblem — givet nogle input, vi ønsker at forudsige en kontinuerlig output.
hypotesen præsenteres normalt som

theta-værdierne er parametrene.
nogle hurtige eksempler på, hvordan vi visualiserer hypotesen:
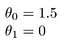
dette giver h (H) = 1,5 + 0 gange. 0 gange betyder ingen hældning, og y vil altid være den konstante 1.5. Dette ligner:

hvad med
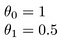

målet med at oprette en model er at vælge parametre eller theta-værdier, så h (H) er tæt på y for træningsdataene, h og y. Så for disse data
x =
y =

jeg vil forsøge at finde en linje med den bedste pasform ved hjælp af lineær regression. Lad os komme i gang.
omkostningsfunktion
vi har brug for en funktion, der minimerer parametrene over vores datasæt. En almindelig funktion, der ofte bruges, er gennemsnitlig kvadreret fejl, som måler forskellen mellem estimatoren (datasættet) og den estimerede værdi (forudsigelsen). Det ser sådan ud:

det viser sig, at vi kan justere ligningen lidt for at gøre beregningen ned ad sporet lidt mere enkel. Vi ender med:
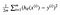
lad os anvende denne const-funktion på følgende data:

For nu vil vi beregne nogle Theta-værdier og plotte omkostningsfunktionen manuelt. Da denne funktion passerer gennem (0, 0), ser vi kun på en enkelt værdi af theta. Fra nu af vil jeg henvise til omkostningsfunktionen som J (Kurt).
for J (1) får vi 0. Ingen overraskelse-en værdi af J(1) giver en lige linje, der passer perfekt til dataene. Hvad med J (0.5)?

MSE-funktionen giver os en værdi på 0, 58. Lad os plotte begge vores værdier hidtil:
J(1) = 0
J (0, 5) = 0.58

jeg vil gå videre og beregne nogle flere værdier af J(Kurt).

og hvis vi slutter prikkerne sammen pænt…

vi kan se, at omkostningsfunktionen er på et minimum, når theta = 1. Dette giver mening-vores oprindelige data er en lige linje med en hældning på 1 (den orange linje i figuren ovenfor).
Gradient Descent
vi minimerede J(liter) ved forsøg og fejl ovenfor — bare forsøger masser af værdier og visuelt inspicere den resulterende graf. Der må være en bedre måde? Kø gradient nedstigning. Gradient nedstigning er en generel funktion til minimering af en funktion, i dette tilfælde den gennemsnitlige kvadrerede Fejlomkostningsfunktion.
Gradient nedstigning dybest set bare gør, hvad vi gjorde i hånden — ændre Theta værdier, eller parametre, bit for bit, indtil vi forhåbentlig ankom et minimum.
vi starter med at initialisere theta0 og theta1 til to værdier, siger 0 for begge, og gå derfra. Formelt er algoritmen som følger:

hvor karrus, alfa, er læringshastigheden, eller hvor hurtigt vi ønsker at bevæge os mod minimumet. Men hvis Kristian er for stor, kan vi gå over stregen.

bringer det hele sammen-lineær Regression
hurtigt opsummering:
vi har en hypotese:

som vi har brug for passer til vores træningsdata. Vi kan bruge en omkostningsfunktion sådan gennemsnitlig kvadreret fejl:

som vi kan minimere ved hjælp af gradientafstamning:

hvilket fører os til vores første maskinlæringsalgoritme, lineær regression. Det sidste stykke af puslespillet, vi skal løse for at have en fungerende lineær regressionsmodel, er det delvise derivat af omkostningsfunktionen:
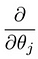
som viser sig at være:
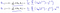
hvilket giver os lineær regression!
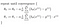
med teorien ude af vejen fortsætter jeg med at implementere denne logik i python i næste indlæg.
Rediger 4.maj: jeg offentliggjorde en opfølgning med fokus på, hvordan Omkostningsfunktionen fungerer her, herunder en intuition, hvordan man beregner den manuelt og to forskellige Python-implementeringer. Jeg kan gøre gradient nedstigning og derefter bringe dem sammen til lineær regression snart.