at finde en optimal løsning til visse optimeringsproblemer kan være en utrolig vanskelig opgave, ofte praktisk umuligt. Dette skyldes, at når et problem bliver tilstrækkeligt stort, er vi nødt til at søge gennem et enormt antal mulige løsninger for at finde den optimale. Selv med moderne computerkraft er der stadig ofte for mange mulige løsninger at overveje. I dette tilfælde, fordi vi ikke realistisk kan forvente at finde den optimale inden for en fornuftig tid, er vi nødt til at nøjes med noget, der er tæt nok.
et eksempel på optimeringsproblem, der normalt har et stort antal mulige løsninger, ville være travelling salesman-problemet. For at finde en løsning på et problem som traveling salesman problem skal vi bruge en algoritme, der er i stand til at finde en god nok løsning i en rimelig tid. I en tidligere tutorial kiggede vi på, hvordan vi kunne gøre dette med genetiske algoritmer, og selvom genetiske algoritmer er en måde, vi kan finde en ‘god nok’ løsning på rejseforhandlerproblemet, er der andre enklere algoritmer, vi kan implementere, som også finder os en tæt på optimal løsning. I denne tutorial er algoritmen, vi bruger, ‘simuleret udglødning’.
hvis du ikke er bekendt med rejseforhandlerproblemet, kan det være værd at tage et kig på min tidligere tutorial, før du fortsætter.
Hvad er simuleret udglødning?
lad os først se på, hvordan simuleret udglødning fungerer, og hvorfor det er godt at finde løsninger på især rejseforhandlerproblemet. Den simulerede udglødningsalgoritme blev oprindeligt inspireret af processen med udglødning i metalarbejde. Udglødning involverer opvarmning og afkøling af et materiale for at ændre dets fysiske egenskaber på grund af ændringerne i dets indre struktur. Når metallet køler, bliver dets nye struktur fast, hvilket får metallet til at bevare sine nyligt opnåede egenskaber. I simuleret udglødning holder vi en temperaturvariabel for at simulere denne opvarmningsproces. Vi oprindeligt sætte det højt og derefter lade det langsomt ‘cool’ som algoritmen kører. Mens denne temperaturvariabel er høj, vil algoritmen med mere frekvens være tilladt at acceptere løsninger, der er værre end vores nuværende løsning. Dette giver algoritmen mulighed for at hoppe ud af eventuelle lokale optimums, den befinder sig tidligt i udførelsen. Efterhånden som temperaturen reduceres, er chancen for at acceptere dårligere løsninger, hvilket gør det muligt for algoritmen gradvist at fokusere på et område i søgeområdet, hvor forhåbentlig en tæt på optimal løsning kan findes. Denne gradvise ‘køleproces’ er det, der gør den simulerede udglødningsalgoritme bemærkelsesværdig effektiv til at finde en tæt på optimal løsning, når man håndterer store problemer, der indeholder adskillige lokale optimums. Karakteren af den rejsende sælger problem gør det til et perfekt eksempel.
fordele ved simuleret udglødning
du undrer dig måske over, om der er nogen reel fordel ved at implementere simuleret udglødning over noget som en simpel bjergbestiger. Selvom bjergbestigere kan være overraskende effektive til at finde en god løsning, har de også en tendens til at sidde fast i lokale optimums. Som vi tidligere har bestemt, er den simulerede udglødningsalgoritme fremragende til at undgå dette problem og er i gennemsnit meget bedre til at finde et omtrentligt globalt optimalt.
for bedre at forstå lad os hurtigt tage et kig på, hvorfor en grundlæggende bakke klatring algoritme er så tilbøjelige til at blive fanget i lokale optimums.
en hill climber algoritme vil simpelthen acceptere nabo løsninger, der er bedre end den nuværende løsning. Når bjergbestigeren ikke kan finde nogen bedre naboer, stopper den.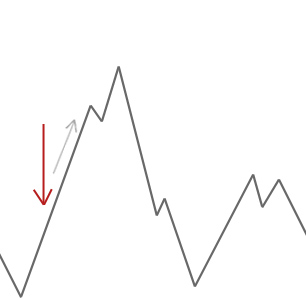
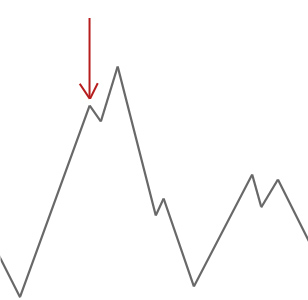
i eksemplet ovenfor starter vi vores bjergbestiger ved den røde pil, og den arbejder sig op ad bakken, indtil den når et punkt, hvor den ikke kan klatre højere uden først at falde ned. I dette eksempel kan vi tydeligt se, at det sidder fast i et lokalt optimalt. Hvis dette var et problem i den virkelige verden, ville vi ikke vide, hvordan søgeområdet ser ud, så desværre ville vi ikke være i stand til at fortælle, om denne løsning er overalt tæt på et globalt optimalt.
simuleret udglødning fungerer lidt anderledes end dette og vil lejlighedsvis acceptere dårligere løsninger. Denne egenskab ved simuleret udglødning hjælper den med at hoppe ud af lokale optimums, som den ellers kunne have sat sig fast i.
Acceptfunktion
lad os se på, hvordan algoritmen beslutter, hvilke løsninger der skal accepteres, så vi bedre kan forstå, hvordan det er i stand til at undgå disse lokale optimums.
først kontrollerer vi, om naboløsningen er bedre end vores nuværende løsning. Hvis det er tilfældet, accepterer vi det ubetinget. Men hvis naboløsningen ikke er bedre, skal vi overveje et par faktorer. For det første, hvor meget værre naboløsningen er; og for det andet, hvor høj den aktuelle ‘temperatur’ i vores system er. Ved høje temperaturer systemet er mere sandsynligt acceptere løsninger, der er værre.
matematikken for dette er ret simpelt:
grundlæggende, jo mindre ændring i energi (opløsningens kvalitet), og jo højere temperatur, jo mere sandsynligt er det for algoritmen at acceptere løsningen.
Algoritmeoversigt
så hvordan ser algoritmen ud? Nå, i sin mest grundlæggende implementering er det ret simpelt.
- først skal vi indstille den indledende temperatur og oprette en tilfældig indledende løsning.
- så begynder vi at løbe, indtil vores stoptilstand er opfyldt. Normalt er systemet enten tilstrækkeligt afkølet, eller der er fundet en god nok løsning.
- herfra vælger vi en nabo ved at foretage en lille ændring af vores nuværende løsning.
- vi beslutter derefter, om vi vil flytte til den naboløsning.
- endelig sænker vi temperaturen og fortsætter looping
temperatur initialisering
for bedre optimering skal vi ved initialisering af temperaturvariablen vælge en temperatur, der oprindeligt giver mulighed for praktisk talt ethvert træk mod den aktuelle løsning. Dette giver algoritmen mulighed for bedre at udforske hele søgeområdet inden afkøling og afvikling i en mere fokuseret region.
eksempelkode
lad os nu bruge det, vi ved, til at oprette en grundlæggende simuleret udglødningsalgoritme og derefter anvende den på traveling salesman-problemet nedenfor. Vi skal bruge Java i denne tutorial, men logikken skal forhåbentlig være enkel nok til at kopiere til ethvert sprog efter eget valg.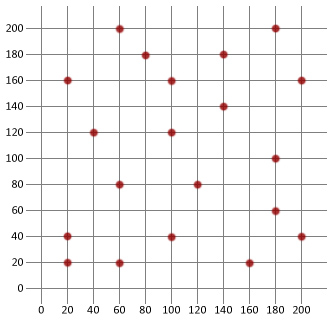
først skal vi oprette en Byklasse, der kan bruges til at modellere de forskellige destinationer for vores rejsende sælger.
by.java
* by.java
* modeller en by
*/
pakke sa;
offentlig klasse by {
int;
int y;
// konstruerer en tilfældigt placeret by
offentlig by () {
dette.= (Int)(matematik.tilfældig ()*200);
dette.y = (Int) (matematik.tilfældig()*200);
}
// konstruerer en by på valgt s, y placering
offentlig by (int s, int y){
dette.
dette.y = y;
}
// Gets city ‘ s koordinat
offentlig int get () {
returner dette.k;
}
// Gets Citys y koordinat
offentlig int getY(){
returner dette.y;
}
// får afstanden til given by
offentlig dobbelt distanceTo (by by){
int afstand = matematik.abs (få () – by.());
int yDistance = matematik.abs (getY () – by.getY ());
dobbelt afstand = matematik.(yDistance*yDistance));
returafstand;
}
@Tilsidesæt
offentlig streng toString () {
return get ()+”, ” + getY();
}
}
næste lad os oprette en klasse, der kan holde styr på byerne.
TourManager.java
* TourManager.java
* holder byerne en tur
*/
pakke sa;
import java.util.ArrayList;
offentlig klasse TourManager {
/ / holder vores byer
privat statisk ArrayList destinationCities = ny ArrayList<by>();
// tilføjer en destinationsby
public static void addCity(City city) {
destinationCities.Tilføj (by);
}
// få en by
offentlig statisk by getCity (int-indeks){
retur (by)destinationCities.få (indeks);
}
// få antallet af destinationsbyer
offentlig statisk int numberOfCities(){
return destinationCities.størrelse();
}
}
nu for at skabe den klasse, der kan modellere en rejsende sælger tur.
tur.java
* tur.java
* gemmer en kandidat tur gennem alle byer
*/
pakke sa;
import java.util.ArrayList;
import java.util.Samlinger;
offentlig klassetur {
/ / holder vores rundvisning i byer
privat ArrayList tour = ny ArrayList<by>();
// Cache
privat int afstand = 0;
// konstruerer en tom tur
offentlig tur(){
til (int i = 0; jeg < TourManager.numberOfCities (); i++) {
tur.Tilføj (null);
}
}
// konstruerer en tur fra en anden tur
offentlig tur(ArrayList tour){
dette.tour = (ArrayList) tour.klon();
}
// return tour information
offentlig ArrayList getTour () {
return tour;
}
// opretter en tilfældig person
public void generateIndividual () {
// Loop gennem alle vores destinationsbyer og tilføj dem til vores tur
for (int cityindeks = 0; cityindeks < TourManager.numberOfCities (); cityindeks++) {
setCity (cityindeks, TourManager.getCity));
}
// tilfældigt omarrangere turen
samlinger.shuffle (tour);
}
// får en by fra turen
offentlig by getCity(int tourPosition) {
return (City)tour.få (tourPosition);
}
// indstiller en by i en bestemt position inden for en tur
public void setCity (int tourPosition, City city) {
tour.set (tourPosition, city);
/ / hvis turene er blevet ændret, skal vi nulstille fitness og afstand
afstand = 0;
}
// får den samlede afstand af turen
offentlig int getDistance () {
if (distance == 0) {
int tourDistance = 0;
// Loop gennem vores tur byer
for (int byindeks=0; byindeks < turstørrelse(); byindeks++) {
// få by vi rejser fra
by fromCity = getCity(byindeks);
// by vi rejser til
by destinationCity;
// Kontroller, at vi ikke er på vores turs sidste by, hvis vi er indstillet vores
// turens endelige destinationsby til vores startby
if(byindeks+1 < turstørrelse()){
destinationcity = getcity(byindeks+1);
}
else {
destinationCity = getCity(0);
}
// Få afstanden mellem de to byer
tourDistance += fromCity.distanceTo (destinationCity);
}
distance = tourDistance;
}
returafstand;
}
// få antallet af byer på vores tur
offentlig int tourstørrelse () {
return tour.størrelse();
}
@Tilsidesæt
offentlig streng toString () {
Strenggenestring=”/”;
for (int i = 0; i < turstørrelse (); i++) {
geneString + = getCity(i)+”|”;
}
retur geneString;
}
}
lad os endelig oprette vores simulerede udglødningsalgoritme.
simuleret Annealing.java
offentlig klasse Simuleretannealing {
/ / Beregn accept Sandsynlighed
offentlig statisk dobbelt acceptsandsynlighed (int energi, int nyenergi, dobbelt temperatur) {
// hvis den nye løsning er bedre, accepter den
if (nyenergi < energi) {
return 1.0;
}
// hvis den nye løsning er værre, beregne en accept Sandsynlighed
return Math.((energi-nyenergi) / temperatur);
}
offentlig statisk void main(String args) {
// Opret og tilføj vores byer
City city = NY by(60, 200);
TourManager.addCity (by);
by city2 = ny by (180, 200);
TourManager.addCity (city2);
by city3 = ny by(80, 180);
TourManager.addCity (city3);
by city4 = ny by(140, 180);
TourManager.addCity(city4);
by city5 = ny by (20, 160);
TourManager.addCity (city5);
by city6 = ny by(100, 160);
TourManager.addCity (city6);
by city7 = ny by(200, 160);
TourManager.addCity (city7);
by city8 = ny by(140, 140);
TourManager.addCity (BY8);
Byby9 = ny by(40, 120);
TourManager.addCity (BY9);
by city10 = ny by(100, 120);
TourManager.addCity(city10);
by city11 = ny by (180, 100);
TourManager.addCity(city11);
by city12 = ny by (60, 80);
TourManager.addCity (city12);
by city13 = ny by(120, 80);
TourManager.addCity(by13);
Byby14 = ny by (180, 60);
TourManager.addCity(by14);
Byby15 = ny by (20, 40);
TourManager.addCity(by15);
Byby16 = ny by (100, 40);
TourManager.addCity(by16);
Byby17 = ny by (200, 40);
TourManager.addCity (city17);
by by18 = ny by (20, 20);
TourManager.addCity(by18);
Byby19 = ny by (60, 20);
TourManager.addCity(by19);
Byby20 = ny by (160, 20);
TourManager.addCity (city20);
// Indstil indledende temp
dobbelt temp = 10000;
// kølehastighed
dobbelt kølehastighed = 0.003;
// Initialiser intial opløsning
Tour currentSolution = ny tur ();
currentSolution.generateIndividual ();
System.uden.println (“Initial solution distance:” + currentSolution.getDistance ());
// Sæt som nuværende bedste
Tour bedste = ny tur(currentSolution.getTour ());
// Loop indtil systemet er afkølet
mens (temp > 1) {
// Opret ny nabotur
Turnyhedsløsning = ny tur (currentSolution.getTour ());
// få en tilfældig position i turen
int tourPos1 = (int) (nyhedsopløsning.turstørrelse () * matematik.tilfældig ());
int tourPos2 = (int) (nyhedsopløsning.turstørrelse () * matematik.tilfældig ());
// få byerne på udvalgte positioner i turen
by byvap1 = nyhedsopløsning.getCity (tourPos1);
Bybysvap2 = nyhedsopløsning.getCity (tourPos2);
// Byt dem
nyhedsopløsning.setCity (tourPos2, byvap1);
nyhedsopløsning.setCity (tourPos1, citysvap2);
// få energi af løsninger
int currentEnergy = currentSolution.getDistance ();
int neighbourEnergy = nyhedsopløsning.getDistance ();
// Beslut om vi skal acceptere naboen
if(acceptanceProbability (currentEnergy, neighbourEnergy, temp) > matematik.tilfældig ()) {
currentSolution = ny tur (nyhedsopløsning.getTour());
}
// Hold styr på den bedste løsning fundet
if (currentSolution.getDistance () < bedst.getDistance ()) {
bedste = ny tur (currentSolution.getTour());
}
// Cool system
temp * = 1-coolingRate;
}
System.uden.println (“endelig løsningsafstand:” + bedst.getDistance ());
System.uden.println (“Tour:” + bedst);
}
}
Output
endelig løsningsafstand: 911
tur: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
konklusion
i dette eksempel var vi i stand til mere end halvdelen af afstanden til vores oprindelige tilfældigt genererede rute. Dette viser forhåbentlig, hvor praktisk denne relativt enkle algoritme er, når den anvendes til visse typer optimeringsproblemer.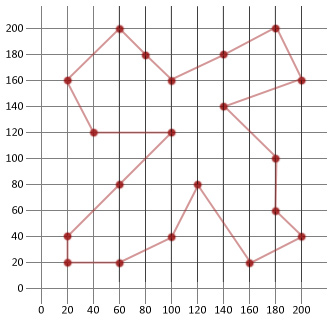
forfatter
 Hej, Jeg er Lee.
Hej, Jeg er Lee.jeg er en udvikler fra Storbritannien, der elsker teknologi og forretning. Her finder du artikler og tutorials om ting, der interesserer mig. Hvis du vil ansætte mig eller vide mere om mig, gå over til min om mig side