Greedy Algorithmus mit Beispielen: Greedy Methode & Ansatz

Um den gierigen Ansatz zu verstehen, müssen Sie über Kenntnisse in Rekursion und Kontextwechsel verfügen. Dies hilft Ihnen zu verstehen, wie Sie den Code verfolgen. Sie können das gierige Paradigma in Bezug auf Ihre eigenen notwendigen und ausreichenden Aussagen definieren.

Zwei Bedingungen definieren das gierige Paradigma.

• Jede schrittweise Lösung muss ein Problem in Richtung seiner am besten akzeptierten Lösung strukturieren.
• Es genügt, wenn die Strukturierung des Problems in einer endlichen Anzahl gieriger Schritte anhalten kann.

Lassen Sie uns mit der Fortsetzung der Theorie die Geschichte beschreiben, die mit dem gierigen Suchansatz verbunden ist.

In diesem Tutorial zum gierigen Algorithmus lernen Sie:

• Geschichte der gierigen Algorithmen
• Gierige Strategien und Entscheidungen
• Merkmale des gierigen Ansatzes
• Warum den gierigen Ansatz verwenden?
• So lösen Sie das Aktivitätsauswahlproblem
• Architektur des gierigen Ansatzes
• Nachteile gieriger Algorithmen

Geschichte der gierigen Algorithmen

Hier ist ein wichtiger Meilenstein der gierigen Algorithmen:

• Gierige Algorithmen wurden in den 1950er Jahren für viele Graph-Walk-Algorithmen konzipiert.
• Esdger Djikstra konzipierte den Algorithmus, um minimale Spannbäume zu erzeugen. Er zielte darauf ab, die Spannweite der Routen innerhalb der niederländischen Hauptstadt Amsterdam zu verkürzen.
• Im selben Jahrzehnt erzielten Prim und Kruskal Optimierungsstrategien, die auf der Minimierung der Wegekosten entlang der Routen basierten.
• In den 70er Jahren schlugen die amerikanischen Forscher Cormen, Rivest und Stein in ihrem Buch classical introduction to algorithms eine rekursive Substruktur gieriger Lösungen vor.
• Das gierige Suchparadigma wurde 2005 als eine andere Art von Optimierungsstrategie in den NIST-Datensätzen registriert.
• Bis heute verwenden Protokolle, die das Web ausführen, wie das Open-Shortest-Path-first (OSPF) und viele andere Netzwerkpaketvermittlungsprotokolle die Greedy-Strategie, um die in einem Netzwerk verbrachte Zeit zu minimieren.

Gierige Strategien und Entscheidungen

Logik in ihrer einfachsten Form wurde auf „gierig“ oder „nicht gierig“ reduziert. Diese Aussagen wurden durch den Ansatz definiert, in jeder Algorithmusstufe voranzukommen.

Zum Beispiel verwendete Djikstras Algorithmus eine schrittweise gierige Strategie, die Hosts im Internet durch Berechnung einer Kostenfunktion identifizierte. Der von der Kostenfunktion zurückgegebene Wert bestimmt, ob der nächste Pfad „gierig“ oder „nicht gierig“ ist.

Kurz gesagt, ein Algorithmus hört auf, gierig zu sein, wenn er zu irgendeinem Zeitpunkt einen Schritt unternimmt, der nicht lokal gierig ist. Die gierigen Probleme hören ohne weiteres Ausmaß der Gier auf.

Merkmale des Greedy-Ansatzes

Die wichtigen Merkmale eines Greedy-Methodenalgorithmus sind:

• Es gibt eine geordnete Liste von Ressourcen mit Kosten- oder Wertzuordnungen. Diese quantifizieren Einschränkungen eines Systems.
• Sie nehmen die maximale Menge an Ressourcen in der Zeit, in der eine Einschränkung gilt.
• Bei einem Aktivitätsplanungsproblem sind die Ressourcenkosten beispielsweise in Stunden angegeben, und die Aktivitäten müssen in serieller Reihenfolge ausgeführt werden.

Warum den gierigen Ansatz verwenden?

Hier sind die Gründe für die Verwendung des gierigen Ansatzes:

• Der gierige Ansatz hat einige Kompromisse, die ihn möglicherweise für die Optimierung geeignet machen.
• Ein prominenter Grund ist, sofort die praktikabelste Lösung zu finden. Wenn im Aktivitätsauswahlproblem (siehe unten) weitere Aktivitäten ausgeführt werden können, bevor die aktuelle Aktivität beendet wird, können diese Aktivitäten innerhalb derselben Zeit ausgeführt werden.
• Ein weiterer Grund besteht darin, ein Problem rekursiv basierend auf einer Bedingung zu teilen, ohne dass alle Lösungen kombiniert werden müssen.
• Im Aktivitätsauswahlproblem wird der Schritt „rekursive Division“ erreicht, indem eine Liste von Elementen nur einmal gescannt und bestimmte Aktivitäten berücksichtigt werden.

So lösen Sie das Aktivitätsauswahlproblem

Im Aktivitätsplanungsbeispiel gibt es für jede Aktivität eine „Start“ – und „End“ -Zeit. Jede Aktivität wird als Referenz durch eine Nummer indiziert. Es gibt zwei Aktivitätskategorien.

1. betrachtete Aktivität: ist die Aktivität, anhand derer die Fähigkeit, mehr als eine verbleibende Aktivität auszuführen, analysiert wird.
2. verbleibende Aktivitäten: Aktivitäten an einem oder mehreren Indizes vor der betrachteten Aktivität.

Die Gesamtdauer gibt die Kosten für die Durchführung der Aktivität an. Das heißt (Finish – Start) gibt uns die Dauer als die Kosten einer Aktivität.

Sie werden lernen, dass die gierige Ausdehnung die Anzahl der verbleibenden Aktivitäten ist, die Sie in der Zeit einer betrachteten Aktivität ausführen können.

Architektur des gierigen Ansatzes

SCHRITT 1)

Scannen Sie die Liste der Aktivitätskosten, beginnend mit Index 0 als betrachtetem Index.

SCHRITT 2)

Wenn bis zum Ende der betrachteten Aktivität weitere Aktivitäten abgeschlossen werden können, suchen Sie nach einer oder mehreren verbleibenden Aktivitäten.

SCHRITT 3)

Wenn keine verbleibenden Aktivitäten mehr vorhanden sind, wird die aktuelle verbleibende Aktivität zur nächsten berücksichtigten Aktivität. Wiederholen Sie Schritt 1 und Schritt 2 mit der neu betrachteten Aktivität. Wenn keine Aktivitäten mehr vorhanden sind, fahren Sie mit Schritt 4 fort.

SCHRITT 4 )

Gibt die Vereinigung der betrachteten Indizes zurück. Dies sind die Aktivitätsindizes, die verwendet werden, um den Durchsatz zu maximieren.

Code-Erklärung

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

Erläuterung des Codes:

1. Enthaltene Header-Dateien / Klassen
2. Eine maximale Anzahl von Aktivitäten, die vom Benutzer bereitgestellt werden.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

Erläuterung des Codes:

1. Der Namespace für Streaming-Vorgänge.
2. Eine Klassendefinition für TIME
3. Ein Stunden-Zeitstempel.
4. Ein Zeitstandardkonstruktor
5. Die Stundenvariable.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

Erläuterung des Codes:

1. Eine Klassendefinition aus Aktivität
2. Zeitstempel Definieren einer Dauer
3. Alle Zeitstempel werden im Standardkonstruktor auf 0 initialisiert

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

Erläuterung des Codes:

1. Teil 1 der Scheduler-Klassendefinition.
2. Der Index ist der Ausgangspunkt für das Scannen des Arrays.
3. Der Initialisierungsindex wird verwendet, um zufällige Zeitstempel zuzuweisen.
4. Mit dem neuen Operator wird ein Array von Aktivitätsobjekten dynamisch zugewiesen.
5. Der scheduled Pointer definiert die aktuelle Basisposition für die Planung.

Scheduler(){ considered_index = 0; scheduled = NULL;......

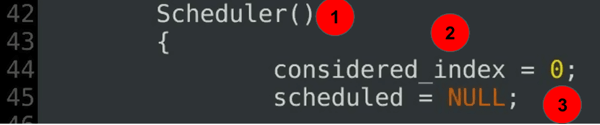
Erläuterung des Codes:

1. Der Scheduler-Konstruktor – Teil 2 der Scheduler-Klassendefinition.
2. Der betrachtete Index definiert den aktuellen Beginn des aktuellen Scans.
3. Die aktuelle gierige Ausdehnung ist zu Beginn nicht definiert.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

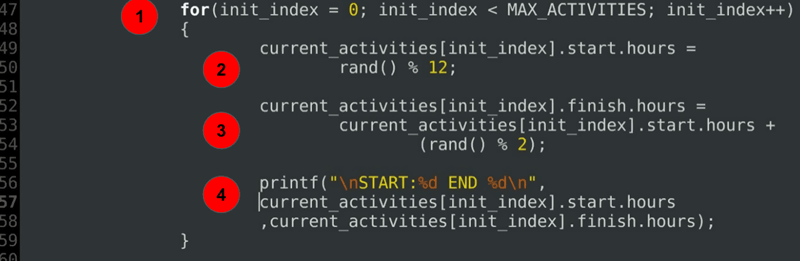
Erläuterung des Codes:

1. Eine for-Schleife zum Initialisieren der Start- und Endstunden jeder der derzeit geplanten Aktivitäten.
2. Startzeit Initialisierung.
3. Endzeitinitialisierung immer nach oder genau zur Startstunde.
4. Eine Debug-Anweisung zum Drucken zugewiesener Dauern.

public: Activity * activity_select(int);};

Erläuterung des Codes:

1. Teil 4 – der letzte Teil der Scheduler-Klassendefinition.
2. Die Select-Funktion nimmt einen Startpunkt-Index als Basis und teilt die gierige Quest in gierige Unterprobleme auf.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. Mit dem Bereichsauflösungsoperator (::) wird die Funktionsdefinition bereitgestellt.
2. Der betrachtete Index ist der nach Wert aufgerufene Index. Das greedy_extent ist das initialisierte nur einen Index nach dem betrachteten Index.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

Erläuterung des Codes:

1. Die Kernlogik – Das gierige Ausmaß ist auf die Anzahl der Aktivitäten beschränkt.
2. Die Startzeiten der aktuellen Aktivität werden als planbar geprüft, bevor die betrachtete Aktivität (angegeben durch den betrachteten Index) beendet wird.
3. Solange dies möglich ist, wird eine optionale Debug-Anweisung gedruckt.
4. Zum nächsten Index im Aktivitätsarray vorrücken

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

Erläuterung des Codes:

1. Die Bedingung prüft, ob alle Aktivitäten abgedeckt wurden.
2. Wenn nicht, können Sie Ihre Anwendung mit dem betrachteten Index als aktuellem Punkt neu starten. Dies ist ein rekursiver Schritt, der die Problemstellung gierig teilt.
3. Wenn ja, kehrt es zum Aufrufer zurück, ohne dass es erweitert werden kann.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

Erläuterung des Codes:

1. Die Hauptfunktion zum Aufrufen des Schedulers.
2. Ein neuer Scheduler wird instanziiert.
3. Die activity Select-Funktion, die einen Zeiger vom Typ activity zurückgibt, kehrt zum Aufrufer zurück, nachdem die gierige Suche beendet ist.

Ausgang:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

Nachteile von gierigen Algorithmen

Es ist nicht für gierige Probleme geeignet, bei denen für jedes Teilproblem wie das Sortieren eine Lösung erforderlich ist.

Bei solchen Greedy-Algorithmus-Übungsproblemen kann die Greedy-Methode falsch sein; im schlimmsten Fall sogar zu einer nicht optimalen Lösung führen.

Daher besteht der Nachteil gieriger Algorithmen darin, nicht zu wissen, was vor dem aktuellen gierigen Zustand liegt.

Unten ist eine Darstellung des Nachteils der gierigen Methode:

In dem gierigen Scan, der hier als Baum gezeigt wird (höherer Wert höhere Gier), wird ein Algorithmuszustand mit dem Wert: 40 wahrscheinlich 29 als nächsten Wert annehmen. Außerdem endet seine Suche um 12 Uhr. Dies entspricht einem Wert von 41.

Wenn der Algorithmus jedoch einen suboptimalen Weg eingeschlagen oder eine Eroberungsstrategie angenommen hat. dann würde auf 25 40 folgen, und die Gesamtkostenverbesserung würde 65 betragen, was als suboptimale Entscheidung um 24 Punkte höher bewertet wird.

Beispiele für gierige Algorithmen

Die meisten Netzwerkalgorithmen verwenden den gierigen Ansatz. Hier ist eine Liste einiger Beispiele für gierige Algorithmen:

• Prims minimaler Spannbaum-Algorithmus
• Travelling Salesman Problem
• Graph – Map Coloring
• Kruskals minimaler Spannbaum-Algorithmus
• Dijkstras minimaler Spannbaum-Algorithmus
• Graph – Vertex-Abdeckung
• Rucksackproblem
• Jobplanungsproblem

Zusammenfassung:

Zusammenfassend definierte der Artikel das gierige Paradigma und zeigte, wie gierige Optimierung und Rekursion Ihnen helfen können, bis zu einem gewissen Punkt die beste Lösung zu finden. Der gierige Algorithmus wird in vielen Sprachen als gieriger Algorithmus Python, C, C #, PHP, Java usw. zur Problemlösung eingesetzt. Das Beispiel für die Aktivitätsauswahl des gierigen Algorithmus wurde als strategisches Problem beschrieben, das mit dem gierigen Ansatz einen maximalen Durchsatz erreichen könnte. Am Ende wurden die Nachteile der Verwendung des gierigen Ansatzes erklärt.