Learn OpenCV

In diesem Beitrag erfahren Sie mehr über den Feature-Deskriptor Histogram of Oriented Gradients (HOG). Wir werden lernen, was unter der Haube steckt und wie dieser Deskriptor intern von OpenCV, MATLAB und anderen Paketen berechnet wird.

Dieser Beitrag ist Teil einer Serie, die ich über Bilderkennung und Objekterkennung schreibe.

Die vollständige Liste der Tutorials in dieser Serie ist unten angegeben:

1. Bilderkennung mit traditionellen Computer Vision Techniken : Teil 1
2. Histogramm orientierter Verläufe: Teil 2
3. Beispielcode für die Bilderkennung: Teil 3
4. Training eines besseren Augendetektors: Teil 4a
5. Objekterkennung mit herkömmlichen Computer-Vision-Techniken: Teil 4b
6. So trainieren und testen Sie Ihren eigenen OpenCV-Objektdetektor: Teil 5
7. Bilderkennung mittels Deep Learning : Teil 6
   • Einführung in neuronale Netze
   • Verständnis Feedforward Neuronale Netze
   • Bilderkennung mit Convolutional Neural Networks
8. Objekterkennung mit Deep Learning : Teil 7

Viele Dinge sehen schwierig und mysteriös aus. Aber sobald Sie sich die Zeit nehmen, sie zu dekonstruieren, wird das Geheimnis durch Meisterschaft ersetzt, und danach streben wir. Wenn Sie ein Anfänger sind und Computer Vision schwer und mysteriös finden, denken Sie einfach an Folgendes

F: Wie isst man einen Elefanten ?
EIN : Ein Bissen nach dem anderen!

Was ist ein Feature Descriptor?

Ein Feature-Deskriptor ist eine Darstellung eines Bildes oder eines Bild-Patches, der das Bild vereinfacht, indem nützliche Informationen extrahiert und überflüssige Informationen weggeworfen werden.

Typischerweise konvertiert ein Feature-Deskriptor ein Bild der Größe width x height x 3 (Kanäle) in einen Feature-Vektor / Array der Länge n. Im Fall des HOG-Feature-Deskriptors hat das Eingabebild die Größe 64 x 128 x 3 und der Ausgabe-Feature-Vektor die Länge 3780.

Denken Sie daran, dass der HOG-Deskriptor für andere Größen berechnet werden kann, aber in diesem Beitrag halte ich mich an die Zahlen im Originalpapier, damit Sie das Konzept anhand eines konkreten Beispiels leicht verstehen können.

Das klingt alles gut, aber was ist „nützlich“ und was ist „fremd“ ? Um „nützlich“ zu definieren, müssen wir wissen, wofür es „nützlich“ ist? Offensichtlich ist der Merkmalsvektor für die Anzeige des Bildes nicht nützlich. Aber es ist sehr nützlich für Aufgaben wie Bilderkennung und Objekterkennung. Der Merkmalsvektor, der von diesen Algorithmen erzeugt wird, wenn er in einen Bildklassifizierungsalgorithmus wie die Support Vector Machine (SVM) eingespeist wird, liefert gute Ergebnisse.

Aber welche Arten von „Funktionen“ sind für Klassifizierungsaufgaben nützlich? Lassen Sie uns diesen Punkt anhand eines Beispiels diskutieren. Angenommen, wir möchten einen Objektdetektor erstellen, der Knöpfe von Hemden und Mänteln erkennt.

Ein Knopf ist kreisförmig (kann in einem Bild elliptisch aussehen) und hat normalerweise ein paar Löcher zum Nähen. Sie können einen Kantendetektor für das Bild einer Schaltfläche ausführen und leicht feststellen, ob es sich um eine Schaltfläche handelt, indem Sie einfach nur das Kantenbild betrachten. In diesem Fall sind Kanteninformationen „nützlich“ und Farbinformationen nicht. Darüber hinaus müssen die Merkmale auch Unterscheidungskraft haben. Zum Beispiel sollten gute Merkmale, die aus einem Bild extrahiert werden, in der Lage sein, den Unterschied zwischen Knöpfen und anderen kreisförmigen Objekten wie Münzen und Autoreifen zu erkennen.

Im HOG-Feature-Deskriptor wird die Verteilung (Histogramme ) von Gradientenrichtungen ( orientierte Gradienten ) als Features verwendet. Gradienten (x- und y-Ableitungen) eines Bildes sind nützlich, da die Größe der Gradienten an Kanten und Ecken (Regionen mit abrupten Intensitätsänderungen) groß ist und wir wissen, dass Kanten und Ecken viel mehr Informationen über die Objektform enthalten als flache Regionen.

Wie berechnet man das Histogramm orientierter Gradienten?

In diesem Abschnitt werden wir auf die Details der Berechnung des HOG-Feature-Deskriptors eingehen. Um jeden Schritt zu veranschaulichen, verwenden wir einen Patch eines Bildes.

Schritt 1 : Vorverarbeitung

Wie bereits erwähnt, wird der für die Fußgängererkennung verwendete HOG-Merkmalsdeskriptor auf einem 64 × 128-Patch eines Bildes berechnet. Natürlich kann ein Bild von beliebiger Größe sein. Typischerweise werden Patches mit mehreren Maßstäben an vielen Bildorten analysiert. Die einzige Einschränkung besteht darin, dass die zu analysierenden Patches ein festes Seitenverhältnis haben. In unserem Fall müssen die Patches ein Seitenverhältnis von 1: 2 haben. Sie können beispielsweise 100 × 200, 128 × 256 oder 1000 × 2000 sein, jedoch nicht 101 × 205.

Um diesen Punkt zu veranschaulichen, habe ich ein großes Bild der Größe 720 × 475 gezeigt. Wir haben einen Patch der Größe 100 × 200 für die Berechnung unseres HOG-Feature-Deskriptors ausgewählt. Dieser Patch wird aus einem Bild herausgeschnitten und auf 64 × 128 verkleinert. Jetzt sind wir bereit, den HOG-Deskriptor für diesen Image-Patch zu berechnen.

Das Papier von Dalal und Triggs erwähnt auch die Gammakorrektur als Vorverarbeitungsschritt, aber die Leistungssteigerungen sind gering und so überspringen wir den Schritt.

Schritt 2: Berechnen Sie die Gradientenbilder

Um einen HOG-Deskriptor zu berechnen, müssen wir zuerst die horizontalen und vertikalen Gradienten berechnen; schließlich wollen wir das Histogramm der Gradienten berechnen. Dies wird leicht erreicht, indem das Bild mit den folgenden Kerneln gefiltert wird.

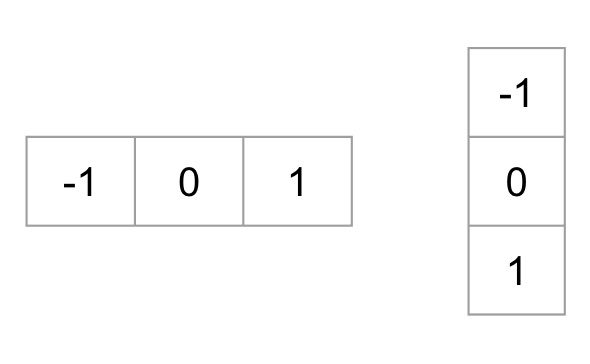
Wir können die gleichen Ergebnisse auch erzielen, indem wir den Sobel-Operator in OpenCV mit Kernelgröße 1 verwenden.

// C++ gradient calculation.// Read imageMat img = imread("bolt.png");img.convertTo(img, CV_32F, 1/255.0);// Calculate gradients gx, gyMat gx, gy;Sobel(img, gx, CV_32F, 1, 0, 1);Sobel(img, gy, CV_32F, 0, 1, 1);

# Python gradient calculation # Read imageim = cv2.imread('bolt.png')im = np.float32(im) / 255.0# Calculate gradientgx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)

Als nächstes können wir die Größe und Richtung des Gradienten anhand der folgenden Formel ermitteln

Wenn Sie OpenCV verwenden, kann die Berechnung mit der Funktion cartToPolar wie unten gezeigt erfolgen.

// C++ Calculate gradient magnitude and direction (in degrees)Mat mag, angle;cartToPolar(gx, gy, mag, angle, 1);

Der gleiche Code in Python sieht so aus.

# Python Calculate gradient magnitude and direction ( in degrees )mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

Die folgende Abbildung zeigt die Verläufe.

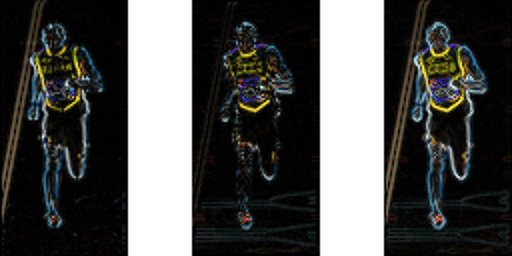
Beachten Sie, dass der x-Gradient auf vertikalen Linien und der y-Gradient auf horizontalen Linien ausgelöst wird. Die Größe von Gradientenbränden, wo immer sich die Intensität stark ändert. Keiner von ihnen feuert, wenn die Region glatt ist. Ich habe das Bild, das die Richtung des Farbverlaufs zeigt, absichtlich weggelassen, da die als Bild gezeigte Richtung nicht viel vermittelt.

Das Verlaufsbild hat viele nicht wesentliche Informationen entfernt (z. B. konstanter farbiger Hintergrund), aber Umrisse hervorgehoben. Mit anderen Worten, Sie können das Verlaufsbild betrachten und trotzdem leicht sagen, dass sich eine Person im Bild befindet.

An jedem Pixel hat der Gradient eine Größe und eine Richtung. Für Farbbilder werden die Gradienten der drei Kanäle ausgewertet ( wie in der Abbildung oben gezeigt). Die Größe des Gradienten an einem Pixel ist das Maximum der Größe der Gradienten der drei Kanäle, und der Winkel ist der Winkel, der dem maximalen Gradienten entspricht.

Schritt 3: Histogramm der Gradienten in 8 × 8 Zellen berechnen

In diesem Schritt wird das Bild in 8 × 8-Zellen unterteilt und für jede 8 × 8-Zelle ein Histogramm von Gradienten berechnet.

Wir werden gleich etwas über die Histogramme lernen, aber bevor wir dorthin gehen, wollen wir zuerst verstehen, warum wir das Bild in 8 × 8-Zellen unterteilt haben. Einer der wichtigsten Gründe für die Verwendung eines Feature-Deskriptors zur Beschreibung eines Patches eines Bildes besteht darin, dass er eine kompakte Darstellung bietet. Ein 8 × 8-Bild-Patch enthält 8x8x3 = 192 Pixelwerte. Der Gradient dieses Patches enthält 2 Werte (Größe und Richtung) pro Pixel, was 8x8x2 = 128 Zahlen ergibt.

Am Ende dieses Abschnitts werden wir sehen, wie diese 128 Zahlen mit einem 9-Bin-Histogramm dargestellt werden, das als Array von 9 Zahlen gespeichert werden kann. Die Darstellung ist nicht nur kompakter, die Berechnung eines Histogramms über einem Patch macht diese Darstellung robuster gegen Rauschen. Einzelne Graidents können Rauschen aufweisen, aber ein Histogramm über 8 × 8-Patch macht die Darstellung viel weniger rauschempfindlich.

Aber warum 8×8 Patch? Warum nicht 32×32 ? Es ist eine Design-Wahl, die von der Skala der Funktionen, die wir suchen, informiert wird. HOG wurde ursprünglich zur Fußgängererkennung verwendet. 8 × 8-Zellen in einem Foto eines Fußgängers im Maßstab 64 × 128 sind groß genug, um interessante Merkmale (z. B. das Gesicht, die Oberseite des Kopfes usw.) aufzunehmen. ).

Das Histogramm ist im Wesentlichen ein Vektor (oder ein Array) von 9 Bins (Zahlen), die Winkeln entsprechen 0, 20, 40, 60 … 160.

Schauen wir uns einen 8 × 8-Patch im Bild an und sehen, wie die Farbverläufe aussehen.

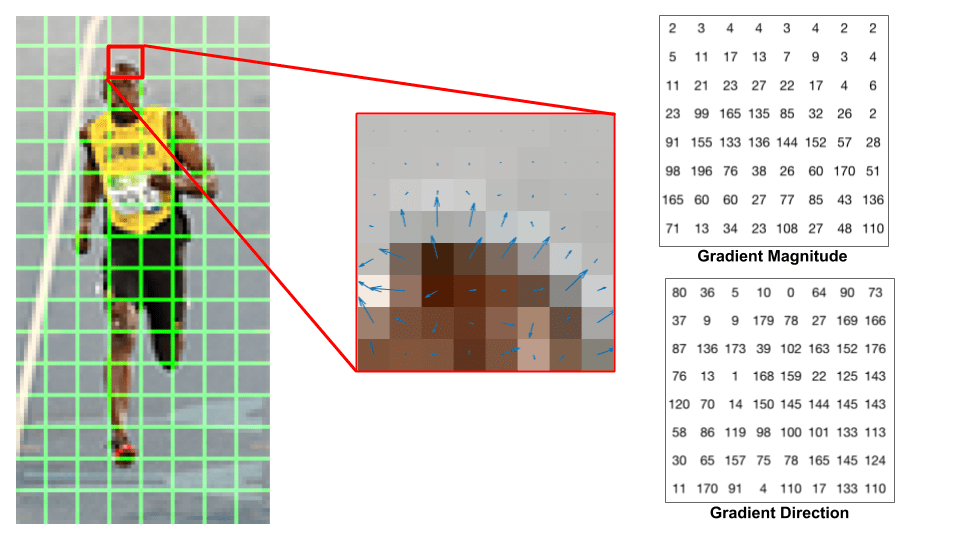
Wenn Sie ein Anfänger in Computer Vision sind, ist das Bild in der Mitte sehr informativ. Es zeigt den Patch des Bildes überlagert mit Pfeilen, die den Gradienten zeigen – der Pfeil zeigt die Richtung des Gradienten und seine Länge zeigt die Größe. Beachten Sie, wie die Richtung der Pfeile auf die Richtung der Intensitätsänderung zeigt und die Größe zeigt, wie groß der Unterschied ist.

Auf der rechten Seite sehen wir die rohen Zahlen, die die Gradienten in den 8 × 8—Zellen mit einem kleinen Unterschied darstellen – die Winkel liegen zwischen 0 und 180 Grad anstelle von 0 bis 360 Grad. Diese werden als „vorzeichenlose“ Farbverläufe bezeichnet, da ein Farbverlauf und sein Negativ durch dieselben Zahlen dargestellt werden. Mit anderen Worten, ein Gradientenpfeil und der 180 Grad gegenüberliegende Pfeil werden als gleich angesehen. Aber warum nicht die 0 – 360 Grad verwenden?

Empirisch hat sich gezeigt, dass unsignierte Gradienten für die Fußgängererkennung besser funktionieren als signierte Gradienten. Bei einigen Implementierungen von HOG können Sie angeben, ob Sie signierte Verläufe verwenden möchten.

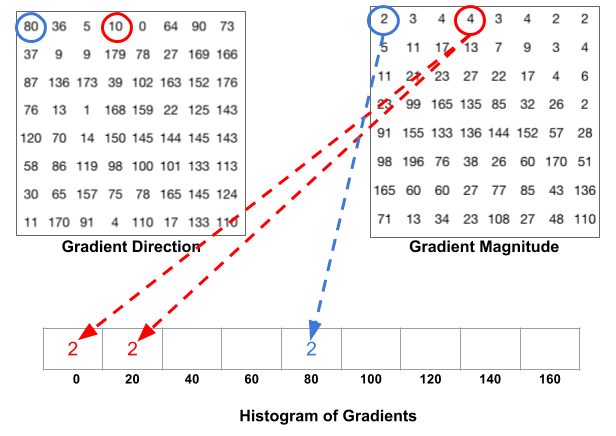
Der nächste Schritt besteht darin, ein Histogramm der Verläufe in diesen 8 × 8-Zellen zu erstellen. Das Histogramm enthält 9 Bins, die den Winkeln 0, 20, 40 … 160 entsprechen. Die folgende Abbildung veranschaulicht den Prozess. Wir betrachten die Größe und Richtung des Gradienten desselben 8 × 8-Patches wie in der vorherigen Abbildung.

Ein Behälter wird basierend auf der Richtung ausgewählt, und die Abstimmung (der Wert, der in den Behälter gelangt) wird basierend auf der Größe ausgewählt. Konzentrieren wir uns zuerst auf das blau eingekreiste Pixel. Es hat einen Winkel ( Richtung) von 80 Grad und eine Magnitude von 2. Es fügt also 2 zum 5. Behälter hinzu. Der Gradient an dem mit Rot eingekreisten Pixel hat einen Winkel von 10 Grad und eine Größe von 4. Da 10 Grad auf halbem Weg zwischen 0 und 20 liegt, teilt sich die Stimme des Pixels gleichmäßig in die beiden Bins auf.

Es gibt noch ein Detail zu beachten. Wenn der Winkel größer als 160 Grad ist, liegt er zwischen 160 und 180, und wir wissen, dass der Winkel 0 und 180 äquivalent macht. Im folgenden Beispiel trägt das Pixel mit einem Winkel von 165 Grad proportional zum 0-Grad-Bin und zum 160-Grad-Bin bei.

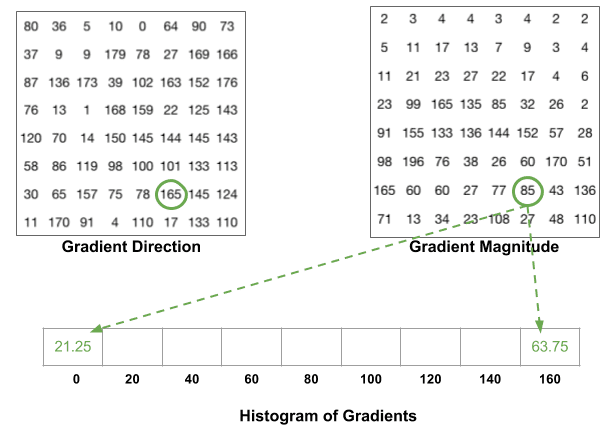
Die Beiträge aller Pixel in den 8 × 8-Zellen werden addiert, um das 9-Bin-Histogramm zu erstellen. Für den Patch oben sieht es so aus

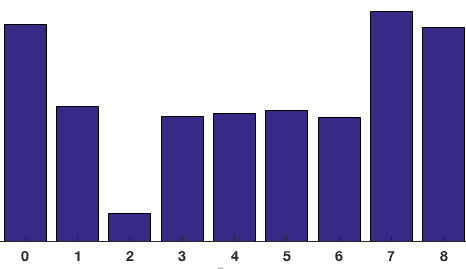
In unserer Darstellung ist die y-Achse 0 Grad. Sie können sehen, dass das Histogramm in der Nähe von 0 und 180 Grad viel Gewicht hat, was nur eine andere Art zu sagen ist, dass die Gradienten im Patch entweder nach oben oder nach unten zeigen.

Schritt 4 : 16 × 16 Block Normalisierung

Im vorherigen Schritt haben wir ein Histogramm basierend auf dem Farbverlauf des Bildes erstellt. Farbverläufe eines Bildes reagieren empfindlich auf die Gesamtbeleuchtung. Wenn Sie das Bild dunkler machen, indem Sie alle Pixelwerte durch 2 dividieren, ändert sich die Gradientengröße um die Hälfte, und daher ändern sich die Histogrammwerte um die Hälfte.

Idealerweise möchten wir, dass unser Deskriptor unabhängig von Beleuchtungsvariationen ist. Mit anderen Worten, wir möchten das Histogramm „normalisieren“, damit sie nicht von Lichtschwankungen betroffen sind.

Bevor ich erkläre, wie das Histogramm normalisiert wird, wollen wir sehen, wie ein Vektor der Länge 3 normalisiert wird.

Nehmen wir an, wir haben einen RGB-Farbvektor . Die Länge dieses Vektors ist $\sqrt{128^2 + 64^2 + 32^2} = 146.64$. Dies wird auch als L2-Norm des Vektors bezeichnet. Wenn wir jedes Element dieses Vektors durch 146,64 dividieren, erhalten wir einen normalisierten Vektor .

Betrachten Sie nun einen anderen Vektor, in dem die Elemente doppelt so groß sind wie der erste Vektor 2 x = . Sie können es selbst herausfinden, um zu sehen, dass die Normalisierung zu einer Normalisierung führt, die der normalisierten Version des ursprünglichen RGB-Vektors entspricht. Sie können sehen, dass die Normalisierung eines Vektors die Skalierung entfernt.

Nun, da wir wissen, wie man einen Vektor normalisiert, könnten Sie versucht sein zu glauben, dass Sie bei der Berechnung von HOG das 9 × 1-Histogramm einfach auf die gleiche Weise normalisieren können, wie wir den 3 × 1-Vektor oben normalisiert haben. Es ist keine schlechte Idee, aber eine bessere Idee ist es, über einen größeren Block von 16 × 16 zu normalisieren.

Ein 16 × 16-Block hat 4 Histogramme, die zu einem 36 x 1-Elementvektor verkettet werden können, und er kann genauso normalisiert werden, wie ein 3 × 1-Vektor normalisiert wird. Das Fenster wird dann um 8 Pixel verschoben (siehe Animation) und ein normalisierter 36 × 1-Vektor wird über dieses Fenster berechnet und der Vorgang wiederholt.

Schritt 5: Berechnen Sie den HOG-Merkmalsvektor

Um den endgültigen Merkmalsvektor für das gesamte Bildfeld zu berechnen, werden die 36 × 1-Vektoren zu einem riesigen Vektor verkettet. Was ist die Größe dieses Vektors? Berechnen wir

1. Wie viele Positionen der 16 × 16 Blöcke haben wir? Es gibt 7 horizontale und 15 vertikale Positionen, was insgesamt 7 x 15 = 105 Positionen ergibt.
2. Jeder 16 × 16-Block wird durch einen 36 ×1-Vektor dargestellt. Wenn wir sie also alle zu einem Gaint-Vektor verketten, erhalten wir einen 36 × 105 = 3780 dimensionalen Vektor.

Histogramm orientierter Verläufe visualisieren

Der HOG-Deskriptor eines Bildflecks wird normalerweise durch Zeichnen der 9 × 1-normalisierten Histogramme in den 8 × 8-Zellen visualisiert. Siehe Bild an der Seite. Sie werden feststellen, dass die Richtung des Histogramms die Form der Person erfasst, insbesondere um den Rumpf und die Beine.

Leider gibt es keine einfache Möglichkeit, den HOG-Deskriptor in OpenCV zu visualisieren.

Abonnieren & Code herunterladen