Ich habe begonnen, Andrew Ngs beliebten maschinellen Lernkurs auf Coursera zu machen. Die erste Woche deckt viel ab, zumindest für jemanden, der seit ein paar Jahren nicht mehr viel Kalkül berührt hat
- Kostenfunktionen (mittlere Differenz im Quadrat)
- Gradientenabstieg
- Lineare Regression
Diese drei Themen waren sehr interessant. Ich werde über jedes im Detail sprechen und wie sie alle zusammenpassen, mit etwas Python-Code zu demonstrieren.
Bearbeiten 4. Mai: Ich habe ein Follow-up veröffentlicht, das sich darauf konzentriert, wie die Kostenfunktion hier funktioniert, einschließlich einer Intuition, wie man sie von Hand berechnet, und zwei verschiedenen Python-Implementierungen. Ich kann Gradientenabstieg machen und sie dann bald für lineare Regression zusammenbringen.
Modelldarstellung
Zunächst besteht das Ziel der meisten Algorithmen für maschinelles Lernen darin, ein Modell zu konstruieren: eine Hypothese, mit der Y basierend auf X geschätzt werden kann. Angenommen, ich trainiere ein Modell basierend auf einer Reihe von Wohnungsdaten, die die Größe des Hauses und den Verkaufspreis enthalten. Indem ich ein Modell trainiere, kann ich Ihnen eine Schätzung geben, wie viel Sie Ihr Haus verkaufen können, basierend auf seiner Größe. Dies ist ein Beispiel für ein Regressionsproblem — angesichts einiger Eingaben möchten wir eine kontinuierliche Ausgabe vorhersagen.
Die Hypothese wird normalerweise wie folgt dargestellt

Die Theta-Werte sind die Parameter.
Einige kurze Beispiele, wie wir die Hypothese visualisieren:
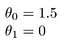
Dies ergibt h(x) = 1,5 + 0x. 0x bedeutet keine Steigung und y ist immer die Konstante 1,5. Das sieht so aus:

Wie wäre es
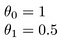

Das Ziel beim Erstellen eines Modells besteht darin, Parameter oder Theta-Werte auszuwählen, sodass h (x) für die Trainingsdaten x und y nahe bei y liegt. Also für diese Daten
x =
y =

Ich werde versuchen, mithilfe der linearen Regression eine Linie mit der besten Anpassung zu finden. Lass uns anfangen.
Kostenfunktion
Wir benötigen eine Funktion, die die Parameter über unseren Datensatz minimiert. Eine häufig verwendete Funktion ist der mittlere quadratische Fehler, der die Differenz zwischen dem Schätzer (dem Datensatz) und dem geschätzten Wert (der Vorhersage) misst. Es sieht so aus:

Es stellt sich heraus, dass wir die Gleichung ein wenig anpassen können, um die Berechnung auf der Strecke etwas einfacher zu gestalten. Wir enden mit:
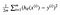
Wenden wir diese konstante Funktion auf die folgenden Daten an:

Im Moment werden wir einige Theta-Werte berechnen und die Kostenfunktion von Hand zeichnen. Da diese Funktion (0, 0) durchläuft, betrachten wir nur einen einzigen Wert von Theta. Von nun an werde ich die Kostenfunktion als J (Θ) bezeichnen.
Für J(1) erhalten wir 0. Kein Wunder – ein Wert von J (1) ergibt eine gerade Linie, die perfekt zu den Daten passt. Wie wäre es mit J (0,5)?

Die MSE-Funktion gibt uns einen Wert von 0,58. Lassen Sie uns beide unsere bisherigen Werte darstellen:
J(1) = 0
J(0,5) = 0.58

Ich werde weitermachen und einige weitere Werte von J (Θ) berechnen.

Und wenn wir die Punkte schön zusammenfügen…

Wir können sehen, dass die Kostenfunktion minimal ist, wenn theta = 1 . Dies ist sinnvoll — unsere Anfangsdaten sind eine gerade Linie mit einer Steigung von 1 (die orangefarbene Linie in der obigen Abbildung).
Gradient Descent
Wir haben J (Θ) durch Versuch und Irrtum minimiert — einfach viele Werte ausprobieren und das resultierende Diagramm visuell untersuchen. Es muss einen besseren Weg geben? Warteschlange Gradienten Abstieg. Gradientenabstieg ist eine allgemeine Funktion zur Minimierung einer Funktion, in diesem Fall die mittlere quadratische Fehlerkostenfunktion.
Gradient Descent macht im Grunde nur das, was wir von Hand gemacht haben — ändern Sie die Theta-Werte oder Parameter Stück für Stück, bis wir hoffentlich ein Minimum erreicht haben.
Wir beginnen mit der Initialisierung von theta0 und theta1 auf zwei beliebige Werte, sagen wir 0 für beide, und gehen von dort aus. Formal ist der Algorithmus wie folgt:

wobei α, alpha die Lernrate ist oder wie schnell wir uns dem Minimum nähern wollen. Wenn α jedoch zu groß ist, können wir überschießen.

Alles zusammenbringen – Lineare Regression
Schnell zusammenfassen:
Wir haben eine Hypothese:

, die wir an unsere Trainingsdaten anpassen müssen. Wir können eine Kostenfunktion wie den mittleren quadratischen Fehler verwenden:

den wir mit Gradient descent minimieren können:

Was uns zu unserem ersten Algorithmus für maschinelles Lernen, der linearen Regression, führt. Das letzte Puzzleteil, das wir lösen müssen, um ein funktionierendes lineares Regressionsmodell zu erhalten, ist die partielle Ableitung der Kostenfunktion:
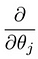
Was sich als:
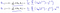
Was uns eine lineare Regression gibt!
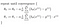
Mit der Theorie aus dem Weg, werde ich diese Logik in Python im nächsten Beitrag implementieren.
Edit 4. Mai: Ich habe ein Follow-up veröffentlicht, das sich darauf konzentriert, wie die Kostenfunktion hier funktioniert, einschließlich einer Intuition, wie man sie von Hand berechnet, und zwei verschiedenen Python-Implementierungen. Ich kann Gradientenabstieg machen und sie dann bald für lineare Regression zusammenbringen.