Eine optimale Lösung für bestimmte Optimierungsprobleme zu finden, kann eine unglaublich schwierige Aufgabe sein, die oft praktisch unmöglich ist. Dies liegt daran, dass wir, wenn ein Problem ausreichend groß wird, eine enorme Anzahl möglicher Lösungen durchsuchen müssen, um die optimale zu finden. Selbst mit moderner Rechenleistung gibt es oft noch zu viele Lösungsmöglichkeiten. In diesem Fall müssen wir uns mit etwas zufrieden geben, das nahe genug ist, da wir nicht realistisch erwarten können, innerhalb einer vernünftigen Zeitspanne das Optimale zu finden.
Ein Beispiel für ein Problem, das normalerweise eine große Anzahl möglicher Lösungen aufweist, wäre das Problem des reisenden Verkäufers. Um eine Lösung für ein Problem wie das Problem des reisenden Verkäufers zu finden, müssen wir einen Algorithmus verwenden, der in der Lage ist, in angemessener Zeit eine ausreichend gute Lösung zu finden. Obwohl genetische Algorithmen eine Möglichkeit sind, eine ausreichend gute Lösung für das Problem des reisenden Verkäufers zu finden, gibt es andere einfachere Algorithmen, die wir implementieren können Finden Sie auch eine nahezu optimale Lösung. In diesem Tutorial verwenden wir den Algorithmus ’simuliertes Glühen‘.
Wenn Sie mit dem Problem des reisenden Verkäufers nicht vertraut sind, lohnt es sich möglicherweise, einen Blick auf mein vorheriges Tutorial zu werfen, bevor Sie fortfahren.
Was ist simuliertes Glühen?
Schauen wir uns zunächst an, wie das simulierte Glühen funktioniert und warum es besonders gut ist, Lösungen für das Problem des reisenden Verkäufers zu finden. Der simulierte Glühalgorithmus wurde ursprünglich vom Glühen in der Metallbearbeitung inspiriert. Beim Glühen wird ein Material erhitzt und gekühlt, um seine physikalischen Eigenschaften aufgrund der Änderungen seiner inneren Struktur zu verändern. Wenn das Metall abkühlt, wird seine neue Struktur fixiert, wodurch das Metall seine neu erhaltenen Eigenschaften beibehält. Beim simulierten Glühen halten wir eine Temperaturvariable, um diesen Erwärmungsprozess zu simulieren. Wir setzen es zunächst hoch und lassen es dann langsam abkühlen, während der Algorithmus läuft. Während diese Temperaturvariable hoch ist, kann der Algorithmus häufiger Lösungen akzeptieren, die schlechter sind als unsere aktuelle Lösung. Dies gibt dem Algorithmus die Möglichkeit, aus jedem lokalen Optimum herauszuspringen, in dem er sich frühzeitig in der Ausführung befindet. Mit abnehmender Temperatur steigt auch die Chance, schlechtere Lösungen zu akzeptieren, so dass sich der Algorithmus allmählich auf einen Bereich des Suchraums konzentrieren kann, in dem hoffentlich eine nahezu optimale Lösung gefunden werden kann. Dieser allmähliche Abkühlungsprozess macht den simulierten Glühalgorithmus bemerkenswert effektiv, um eine nahezu optimale Lösung zu finden, wenn es um große Probleme geht, die zahlreiche lokale Optimierungen enthalten. Die Art des Problems des reisenden Verkäufers macht es zu einem perfekten Beispiel.
Vorteile des simulierten Glühens
Sie fragen sich vielleicht, ob es einen wirklichen Vorteil gibt, das simulierte Glühen gegenüber einem einfachen Bergsteiger zu implementieren. Obwohl Bergsteiger überraschend effektiv sein können, um eine gute Lösung zu finden, neigen sie auch dazu, in lokalen Optimums stecken zu bleiben. Wie wir bereits festgestellt haben, kann der simulierte Glühalgorithmus dieses Problem hervorragend vermeiden und ist im Durchschnitt viel besser darin, ein ungefähres globales Optimum zu finden.
Um besser zu verstehen, lassen Sie uns schnell einen Blick darauf werfen, warum ein grundlegender Algorithmus zum Bergsteigen so anfällig dafür ist, sich in lokalen Optimierungen zu verfangen.
Ein Bergsteiger-Algorithmus akzeptiert einfach Nachbarlösungen, die besser sind als die aktuelle Lösung. Wenn der Bergsteiger keine besseren Nachbarn findet, hört er auf.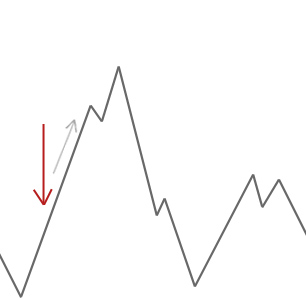
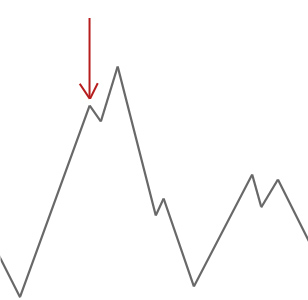
Im obigen Beispiel starten wir unseren Hill Climber am roten Pfeil und er arbeitet sich den Hügel hinauf, bis er einen Punkt erreicht, an dem er nicht höher klettern kann, ohne vorher abzusteigen. In diesem Beispiel können wir deutlich sehen, dass es in einem lokalen Optimum steckt. Wenn dies ein reales Problem wäre, würden wir nicht wissen, wie der Suchraum aussieht, so dass wir leider nicht sagen könnten, ob diese Lösung einem globalen Optimum nahe kommt.
Simuliertes Glühen funktioniert etwas anders und akzeptiert gelegentlich schlechtere Lösungen. Diese Eigenschaft des simulierten Glühens hilft ihm, aus jedem lokalen Optimum herauszuspringen, in dem es sonst stecken geblieben wäre.
Akzeptanzfunktion
Werfen wir einen Blick darauf, wie der Algorithmus entscheidet, welche Lösungen akzeptiert werden sollen, damit wir besser verstehen können, wie diese lokalen Optimierungen vermieden werden können.
Zuerst prüfen wir, ob die Nachbarlösung besser ist als unsere aktuelle Lösung. Wenn ja, akzeptieren wir es bedingungslos. Wenn jedoch die Nachbarlösung nicht besser ist, müssen wir einige Faktoren berücksichtigen. Erstens, wie viel schlimmer die Nachbarlösung ist; und zweitens, wie hoch die aktuelle ‚Temperatur‘ unseres Systems ist. Bei hohen Temperaturen ist das System eher akzeptieren Lösungen, die schlechter sind.
Die Mathematik dafür ist ziemlich einfach:
Grundsätzlich gilt: Je kleiner die Energieänderung (die Qualität der Lösung) und je höher die Temperatur, desto wahrscheinlicher ist es, dass der Algorithmus die Lösung akzeptiert.
Algorithmusübersicht
Wie sieht der Algorithmus aus? Nun, in seiner grundlegendsten Implementierung ist es ziemlich einfach.
- Zuerst müssen wir die Anfangstemperatur einstellen und eine zufällige Anfangslösung erstellen.
- Dann beginnen wir mit der Schleife, bis unsere Stoppbedingung erfüllt ist. Normalerweise ist entweder das System ausreichend gekühlt oder es wurde eine ausreichend gute Lösung gefunden.
- Von hier aus wählen wir einen Nachbarn aus, indem wir eine kleine Änderung an unserer aktuellen Lösung vornehmen.
- Wir entscheiden dann, ob wir zu dieser Nachbarlösung wechseln.
- Zum Schluss senken wir die Temperatur und fahren mit der Schleife fort
Temperaturinitialisierung
Zur besseren Optimierung sollten wir bei der Initialisierung der Temperaturvariablen eine Temperatur auswählen, die anfänglich praktisch jede Bewegung gegen die aktuelle Lösung zulässt. Dies gibt dem Algorithmus die Möglichkeit, den gesamten Suchraum besser zu erkunden, bevor er abkühlt und sich in einer fokussierteren Region niederlässt.
Beispielcode
Lassen Sie uns nun das, was wir wissen, verwenden, um einen grundlegenden simulierten Glühalgorithmus zu erstellen, und ihn dann auf das unten stehende Problem des reisenden Verkäufers anwenden. Wir werden Java in diesem Tutorial verwenden, aber die Logik sollte hoffentlich einfach genug sein, um sie in eine beliebige Sprache Ihrer Wahl zu kopieren.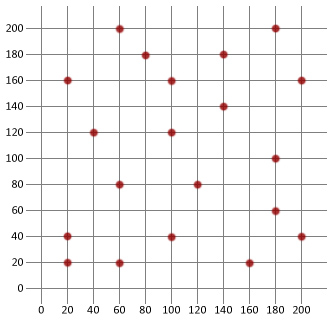
Zuerst müssen wir eine Stadtklasse erstellen, mit der die verschiedenen Ziele unseres reisenden Verkäufers modelliert werden können.
Stadt.java
* Stadt.java
* Modelliert eine Stadt
*/
Paket sa;
öffentliche Klasse City {
int x;
int y;
// Konstruiert eine zufällig platzierte Stadt
public City(){
this.x = (int)(Math.random()*200);
dies.y = (int)(Math.random()*200);
}
// Konstruiert eine Stadt an der gewählten x, y-Position
public City(int x, int y){
this .x = x;
dies.y = y;
}
// Ruft die x-Koordinate der Stadt ab
public int getX(){
gibt dies zurück.x;
}
// Ruft die y-Koordinate der Stadt ab
public int getY(){
return this.y;
}
// Ruft die Entfernung zu einer bestimmten Stadt ab
public double distanceTo(City city){
int xDistance = Math.abs(getX() – Stadt.getX());
int yDistance = Math.abs(getY() – Stadt.getY());
doppelte Entfernung = Math.sqrt( (xDistance * xDistance) + (yDistance * yDistance) );
zurück abstand;
}
@Überschreiben
öffentliche String toString(){
rückkehr getX() +“, „+getY();
}
}
Als nächstes erstellen wir eine Klasse, die die Städte im Auge behalten kann.
TourManager.java
* TourManager.java
* Enthält die Städte einer Tour
*/
Paket sa;
java importieren.util.ArrayList;
public class TourManager {
// Hält unsere Städte
private statische ArrayList destinationCities = neue ArrayList<Stadt>();
// Fügt eine Zielstadt hinzu
public static void addCity(City city) {
destinationCities.hinzufügen(Stadt);
}
// Holen Sie sich eine Stadt
public static City getCity(int index){
return (City)destinationCities.get(index);
}
// Holen Sie sich die Anzahl der Zielstädte
public static int numberOfCities(){
return destinationCities.größe();
}
}
Erstellen Sie nun die Klasse, die eine Traveling Salesman Tour modellieren kann.
Führung.java
* Tour.java
* Speichert eine Kandidatentour durch alle Städte
*/
Paket sa;
java importieren.util.ArrayList;
Java importieren.util.Sammlungen;
public class Tour{
// Hält unsere Tour durch Städte
private ArrayList tour = neue ArrayList<Stadt>();
// Cache
private int distance = 0;
// Erstellt eine leere Tour
public Tour(){
für (int i = 0; i < TourManager.numberOfCities(); i++) {
}.hinzufügen (null);
}
}
// Konstruiert eine Tour aus einer anderen Tour
öffentliche Tour(ArrayList tour){
this.tour = (ArrayList) tour.klonen();
}
// Gibt Tourinformationen zurück
public ArrayList getTour(){
Tour zurückgeben;
}
// Erstellt ein zufälliges Individuum
public void generateIndividual() {
// Schleife durch alle unsere Zielstädte und füge sie zu unserer Tour hinzu
für (int CityIndex = 0; CityIndex < TourManager.numberOfCities(); CityIndex++) {
setCity(CityIndex, TourManager.getCity(CityIndex));
}
// Ordnen Sie die Tour
-Sammlungen nach dem Zufallsprinzip neu an.shuffle(tour);
}
// Ruft eine Stadt von der Tour ab
öffentliche Stadt getCity(int tourPosition) {
return (City)tour.holen Sie sich (Tour));
}
// Setzt eine Stadt an eine bestimmte Position innerhalb einer Tour
public void setCity(int tourPosition, City city) {
tour.set(tourPosition, city);
// Wenn die Touren geändert wurden, müssen wir die Fitness und die Entfernung zurücksetzen
Entfernung = 0;
}
// Ruft die Gesamtstrecke der Tour ab
public int getDistance(){
if (distance == 0) {
int tourDistance = 0;
// Schleife durch die Städte unserer Tour
for (int CityIndex=0; CityIndex < tourSize(); CityIndex++) {
// Holen Sie sich die Stadt, von der wir reisen
Stadt fromCity = getCity(CityIndex);
// Stadt, in die wir reisen
Stadt destinationCity;
// Überprüfen Sie, ob wir uns nicht in der letzten Stadt unserer Tour befinden, wenn wir unsere
// Endzielstadt der Tour auf unsere Startstadt setzen
if( CityIndex+1 < tourSize()){
destinationCity = getCity(CityIndex+1);
}
sonst{
destinationCity = getCity(0);
}
// Ermitteln Sie die Entfernung zwischen den beiden Städten
tourDistance += fromCity.distanceTo(destinationCity);
}
Entfernung = Tourdistanz;
}
rückkehr abstand;
}
// Holen Sie sich die Anzahl der Städte auf unserer Tour
public int tourSize() {
return tour.größe();
}
@ Überschreiben Sie
public String toString() {
String geneString = „/“;
für (int i = 0; i < tourSize(); i++) {
geneString += getCity(i)+“|“;
}
rückkehr geneString;
}
}
Zum Schluss erstellen wir unseren simulierten Glühalgorithmus.
Simuliertes Glühen.java
public class SimulatedAnnealing {
// Berechne die Akzeptanzwahrscheinlichkeit
public static double acceptanceProbability(int energy, int newEnergy, double temperature) {
// Wenn die neue Lösung besser ist, akzeptiere sie
if (newEnergy < energy) {
return 1.0;
}
// Wenn die neue Lösung schlechter ist, berechnen Sie eine Akzeptanzwahrscheinlichkeit
return Math.exp((energy – newEnergy) / temperature);
}
public static void main(String args) {
// Erstellen und fügen Sie unsere Städte hinzu
Stadt Stadt = neue Stadt(60, 200);
TourManager.addCity(Stadt);
Stadt city2 = neue Stadt(180, 200);
TourManager.addCity(city2);
Stadt city3 = neue Stadt(80, 180);
TourManager.addCity(city3);
Stadt city4 = neue Stadt(140, 180);
TourManager.addCity(city4);
Stadt city5 = neue Stadt(20, 160);
TourManager.addCity(city5);
Stadt city6 = neue Stadt(100, 160);
TourManager.addCity(city6);
Stadt city7 = neue Stadt(200, 160);
TourManager.addCity(city7);
Stadt city8 = neue Stadt(140, 140);
TourManager.addCity(city8);
Stadt city9 = neue Stadt(40, 120);
TourManager.Stadt hinzufügen(city9);
Stadt city10 = neue Stadt(100, 120);
TourManager.addCity(city10);
Stadt city11 = neue Stadt(180, 100);
TourManager.addCity(city11);
Stadt city12 = neue Stadt(60, 80);
TourManager.addCity(city12);
Stadt city13 = neue Stadt(120, 80);
TourManager.addCity(city13);
Stadt city14 = neue Stadt(180, 60);
TourManager.addCity(city14);
Stadt city15 = neue Stadt(20, 40);
TourManager.addCity(city15);
Stadt city16 = neue Stadt(100, 40);
TourManager.addCity(city16);
Stadt city17 = neue Stadt(200, 40);
TourManager.Stadt hinzufügen(city17);
Stadt city18 = neue Stadt(20, 20);
TourManager.addCity(city18);
Stadt city19 = neue Stadt(60, 20);
TourManager.addCity(city19);
Stadt city20 = neue Stadt(160, 20);
TourManager.addCity (city20);
//Set initial temp
doppel temp = 10000;
//Kühlung rate
doppel coolingRate = 0,003;
//Initialisieren initial lösung
Tour currentSolution = neue Tour ();
currentSolution.generateIndividual();
System.aus.println(„Anfängliche Lösungsentfernung: “ + Aktuelle Lösung.getDistance());
// Als aktuelle beste
Tour beste = neue Tour(currentSolution.getTour());
// Schleife bis das System abgekühlt ist
while (temp > 1) {
// Neue Nachbartour erstellen
Tour newSolution = neue Tour(currentSolution.getTour());
// Holen Sie sich eine zufällige Positionen in der Tour
int tourPos1 = (int) (newSolution.tourSize() * Math.random());
int tourPos2 = (int) (newSolution.tourSize() * Math.random());
// Holen Sie sich die Städte an ausgewählten Positionen in der Tour
Stadt citySwap1 = newSolution.getCity(tourPos1);
Stadt citySwap2 = newSolution.getCity(tourPos2);
// Tauschen Sie sie aus
newSolution.setCity(tourPos2, citySwap1);
Neue Lösung.setCity(tourPos1, citySwap2);
// Energie der Lösungen abrufen
int currentEnergy = currentSolution.getDistance();
int_energy = newSolution.getDistance();
// Entscheide, ob wir den Nachbarn akzeptieren sollen
if (acceptanceProbability(currentEnergy, neighbourEnergy, temp) > Math.random()) {
currentSolution = neue Tour(newSolution.getTour());
}
// Verfolgen Sie die beste gefundene Lösung
if (currentSolution.getDistance() < am besten.getDistance()) {
best = neue Tour (Aktuelle Lösung.getTour());
}
// Kühles System
temp *= 1-Kühlrate;
}
System.aus.println(„Endgültige Lösung Abstand: “ + best.getDistance());
System.aus.println(„Tour: “ + beste);
}
}
Ausgabe
Endgültige Lösungsentfernung: 911
Tour: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
Fazit
In diesem Beispiel konnten wir mehr als die Hälfte der Strecke unserer anfänglich zufällig generierten Route zurücklegen. Dies zeigt hoffentlich, wie praktisch dieser relativ einfache Algorithmus ist, wenn er auf bestimmte Arten von Optimierungsproblemen angewendet wird.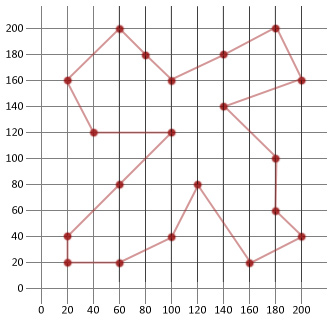
Autor
 Hallo, ich bin Lee.
Hallo, ich bin Lee.Ich bin ein Entwickler aus Großbritannien, der Technologie und Business liebt. Hier finden Sie Artikel und Tutorials zu Dingen, die mich interessieren. Wenn Sie mich einstellen oder mehr über mich erfahren möchten, besuchen Sie meine über mich Seite