Vereinfachung der FEA-Modelle: Flugzeugspannung und Flugzeugdehnung

Anmerkung des Herausgebers: Tony Abbey unterrichtet Live-NAFEMS-FEA-Kurse in den USA, Europa und Asien. Er unterrichtet auch NAFEMS E-Learning-Kurse weltweit. Kontakt .Einzelheiten.

In einem früheren Desktop Engineering-Artikel („Simplify FEA Simulation Models Using Planar Symmetry“) wurde erläutert, dass selbst bei leistungsfähigen modernen Computern häufig die Motivation besteht, vereinfachende Techniken in der strukturellen Finite-Elemente-Analyse (FEA) einzusetzen. Dieses Follow-up beschreibt, wie zwei eng verwandte Methoden verwendet werden können, um 2D-Schnitte durch eine komplexe Struktur in interessierenden Regionen zu erstellen. Die resultierenden FEA-Modelle können wertvolle Einblicke in lokale Spannungen schneller und effizienter geben als ein vollständiges 3D-Modell. Sie erzählen nicht die ganze Geschichte, sind aber wertvolle Werkzeuge für den CAE-Ingenieur.

Die beiden FEA-Methoden werden Plane Stress und plane strain genannt. Beide verwenden 2D-Planarelemente, die wie dünne Schalenelemente aussehen und mit planarer Oberflächengeometrie vermascht sind.

Ebene Spannungsanalyse

Abb. 1 zeigt die wichtigen Fakten zur Planspannungsanalyse. Es wird angenommen, dass der Strukturbereich in der 2D-xy-Ebene liegt, wobei die dritte Strukturdimension relativ klein ist. In der Abbildung ist dies die Dicke in z-Richtung. Spannungen existieren in der 2D-Ebene als Sigma x, Sigma y (direkte Spannungen) und Sigma xy (Schubspannung in der Ebene). Jede dieser Spannungen ist durch die Dicke konstant, wie im Einsatz gezeigt. Außerdem kann es keine Spannung in z-Richtung geben. Diese Spannungs-Dehnungs-Materialbeziehung wird in 2D-Ebenen-Spannungselementen definiert, die bei dieser Art der Analyse verwendet werden.

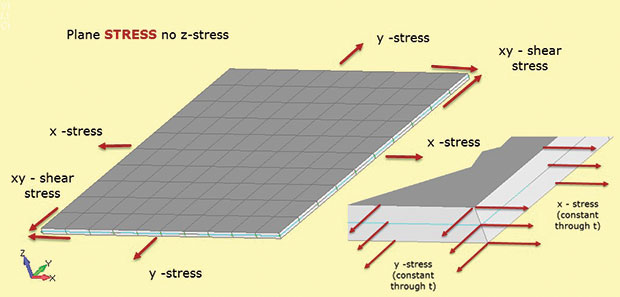Abb. 1: Flugzeug Stress; Stresszustand Annahmen.

Das Fehlen der Z-Spannung ist der Weg, um sich an die Elementtypbezeichnung plane Stress zu erinnern (dh nur Spannungen in der Ebene sind zulässig). Es treten auch keine Durchschiebespannungen auf. Wir könnten das ebene Spannungsmodell in Abb. 1 mit einer biaxialen Last und berechnen Sie Sigma x und Sigma y. Es gibt kein Sigma z. Wir können auch die entsprechenden In-Plane-Dehnungen e-x und e-y berechnen. Dies ist nicht Null, da das Modell frei ist, sich in z zu verdünnen, während es sich in x und y ausdehnt. In einigen Lösern können wir die durchgehende Dickendehnung e-z wiederherstellen und daraus die Dickenänderung berechnen. (Wenn sich das Modell in biaxialer Kompression befindet, wird der z-Abschnitt dicker). Dies wird normalerweise als Sekundärdehnung angesehen und steht möglicherweise nicht zur Ausgabe zur Verfügung — es ist jedoch vorhanden und kann bei Bedarf manuell berechnet werden.

Abb. 2 zeigt ein Aluminium-Laschenbauteil. Die Lasche ragt aus einer Verbundblechlage heraus, die Lagen aufweist, die über den Zapfen (oder Beinen) und dem unteren Körperabschnitt positioniert und verklebt sind. Die Zapfen übertragen die auf die Lasche aufgebrachte Last in die Verbundstruktur. In der Praxis würden die Lagen gestuft sein, um eine reibungslose Scherübertragung durch die Verbindung in den Verbund zu ermöglichen. Die Scherübertragung in den Verbund wird hier durch diffuse Flächenzugkräfte simuliert, die an den Zapfen „ziehen“. Diese gleichen die angelegte Stollenlast aus.

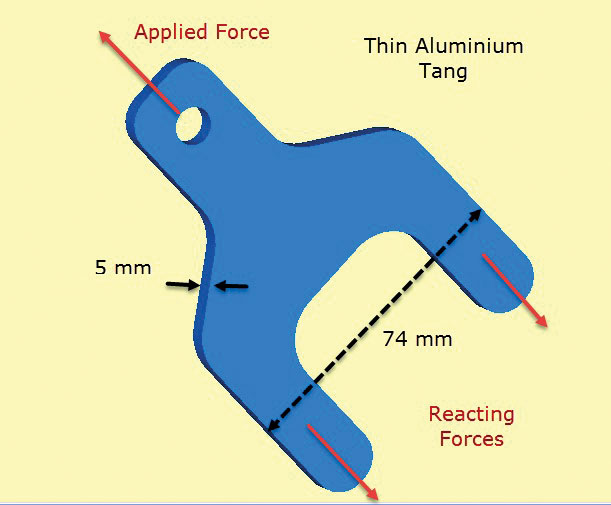Abb. 2: Dünnwandiger Aluminiumrahmen, der Last in zusammengesetzte Struktur überträgt.

Die Schlüsselannahme hier ist, dass durch die Dicke Spannungen Null sind und die Spannungen in der Ebene durch die Dicke im Bauteil konstant sind. Dies bedeutet, dass das lokale Detail der Scherlastübertragung von Verbundwerkstoff zu Tang schlecht modelliert ist. Der Schwerpunkt dieser Analyse liegt jedoch auf der Überprüfung der Dimensionierung von Laschen- und Zapfenquerschnitt frei von dem Verbundwerkstoff, unter Verwendung von Spannungen in der Ebene.

Die Dicke des Bauteils ist im Vergleich zu anderen Abmessungen gering. Dieser Wert wird als tatsächliche Dicke in der Definition des ebenen Spannungselements eingegeben.

Abb. 3 zeigt das FEA-Modell und die berechneten maximalen Hauptspannungen. Die Bereiche von Interesse sind um die Nase und die Schulterradien. In der realen Welt wäre der Spannungszustand bei den Spannungskonzentrationen 3D und durch die Dicke würden sich Sigma-z-Spannungen und Scherspannungen lokal ausgleichen. Es ist hier jedoch sehr sinnvoll anzunehmen, dass die In-Plane-Spannungen dominieren. Dies ist die gleiche Annahme, die in den meisten traditionellen Berechnungen der Spannungskonzentration (Kt) in Handbüchern enthalten ist.

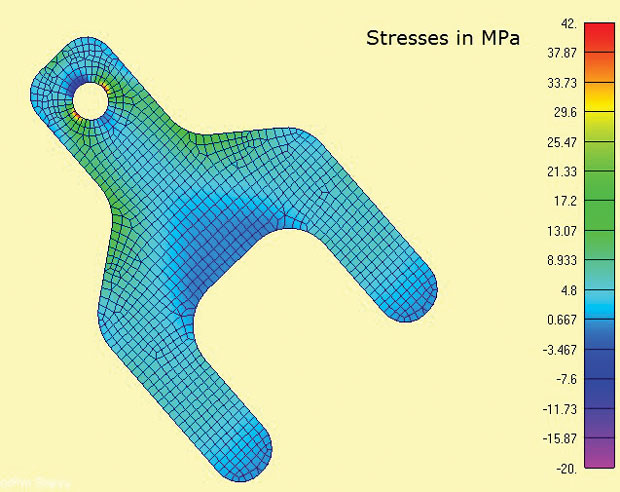Abb. 3: 2D-Spannungselemente mit maximalen Hauptspannungen

Eines der praktischen Merkmale der ebenen Spannungsanalyse ist, dass es sich um eine rein 2D-Analyse handelt, sodass nur drei Freiheitsgrade (DOF) eingeschränkt werden müssen (In-Plane-Translationen x, y und Rotation um die z-Achse). Dies eignet sich für die 3-2-1-Mindesteinschränkungsmethode mit ausgeglichener Last. In einem 2D-Fall degeneriert dies zu einer 2-1-Methode. Ein Knoten hat DOF x und y eingeschränkt, ein zweiter geeigneter orthogonaler Knoten hat DOF x eingeschränkt. Dadurch kann die Reaktionslast in den Zapfen direkt als diffuse Ausgleichslasten aufgebracht werden. Es wäre schwierig, diese Randbedingung über Einschränkungen auf Masse zu simulieren.

Die Durchgangsdicke e-z-Dehnung und damit Ausdünnung der Zapfen konnte als sekundärer Effekt berechnet werden.

Ebene Dehnungsanalyse

Abb. 4 zeigt das Wesen der planaren Dehnungsmethode. Auch hier werden 2D-planare Elemente verwendet, jedoch mit subtil unterschiedlichen Annahmen. Die In-Plane-Spannungen x, y und xy werden wie zuvor entwickelt. Diesmal ist es jedoch die Out-of-Plane- oder Through-Thickness-z-Dehnung, die auf Null gesetzt wird. Die Analyse der ebenen Dehnung erlaubt also nur Dehnungen in der Ebene. Dies funktioniert gut, um dicke Strukturen wie gezeigt darzustellen. Das Vorhandensein von so viel Material neigt dazu, das Bauteil zu stabilisieren und zu verhindern, dass es sich in z. Dies bedeutet auch, dass konstante Spannungen durch die Dicke z in der Struktur entwickelt werden. Diese Spannungs-Dehnungs-Materialbeziehung wird in 2D-Ebenen-Dehnungselementen definiert, die bei dieser Art der Analyse verwendet werden.

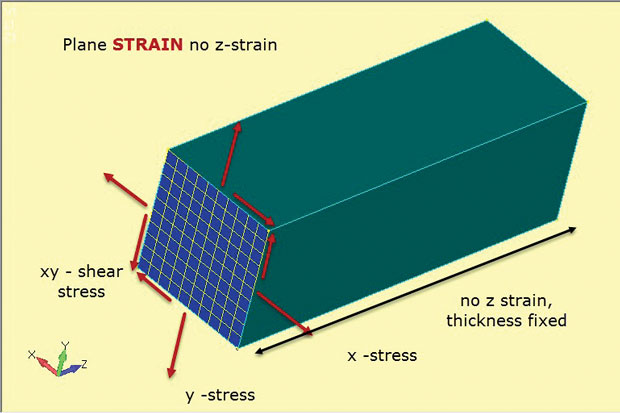Abb. 4: Plane Dehnungsanalyse; Spannungs- und Dehnungszustandsannahmen.

Die Abbildung zeigt die Ausrichtung der Dehnungselemente der 2D-Ebene als Schnitt durch ein typisches tiefes Bauteil. Es wird davon ausgegangen, dass der Spannungszustand an diesem Schnittabschnitt an jedem Schnitt in der xy-Ebene (z-Station) durch das Bauteil dupliziert wird. Das Bauteil wird über seine Länge als prismatisch (mit konstantem Querschnitt) angenommen.

In der Praxis verwenden wir diese Methode, bei der der Spannungszustand in einem tiefen Bauteil langsam von Ebene zu Ebene variiert. Es sollte genügend Materialdurchgangstiefe vorhanden sein, um die Durchgangsbelastung zu stabilisieren und zu beseitigen. Dieses ist das gleiche Prinzip, das auf Bruchzähigkeitsproben verwendet wird, die in Fig. 5. Für den mittleren Abschnitt der dicken Probe ist ein Versagen unter ebenen Dehnungsbedingungen dargestellt. Das Versagen an den freien Kanten und dem Dünnschnitt ist ein anderer Modus, eher wie ein ebener Spannungszustand. Ein ebenes Dehnungs-FEA-Modell wäre definitionsgemäß eine gute Darstellung des Verhaltens der mittelliniendicken Probe, nicht jedoch der freien Kanten oder der dünnen Probe.

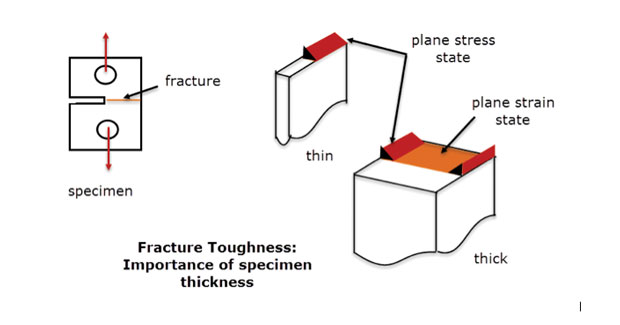Abb. 5: Bruchzähigkeitsproben; dünne und dicke Abschnitte.

Abb. 6 zeigt ein weiteres Bauteil, das in einer Verbundstruktur verwendet wird und eine Klebeverbindung bildet. Hier ist der Abschnitt konstant und tief genug, so dass wir annehmen können, dass die Spannungen auch mit der Tiefe konstant sind. Die freien Stirnflächen (bei + z, -z) haben einen anderen lokalen Spannungszustand (tatsächlich ebene Spannung, wie erwähnt), jedoch ist das Ziel dieser Analyse, die Nettoschnittsspannungen auf der Mittellinie (z = 0) zu überprüfen.

Das 2D-Flächen-Dehnungsanalysegitter ist in Abb. 7. Der Schnitt wird an der Station z = 0 definiert.

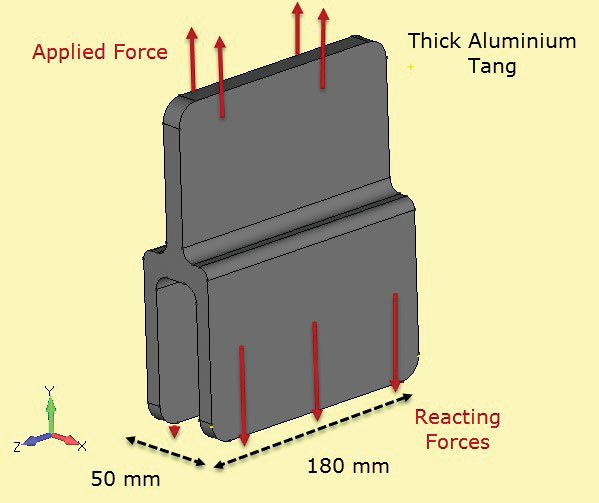Abb. 6: Tiefgezogener Aluminiumzapfen.

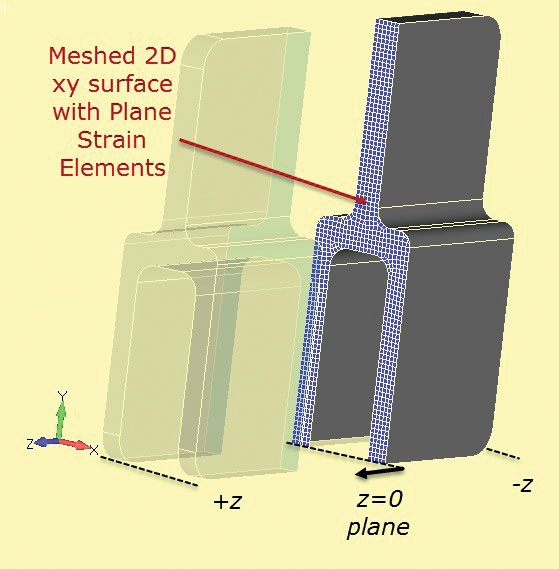Abb. 7: Schnitt Schnitt durch festen Abschnitt, um 2D-Ebene Dehnungsabschnitt zu entwickeln.

Es kann ein sehr feines 2D-Flächen-Dehnungsnetz verwendet werden, das im Vergleich zu einem vollständigen 3D-Modell sehr schnell abläuft. Die 2-1-Einschränkungsmethode wird wie zuvor verwendet. Die Beladung muss sorgfältig abgewogen werden. Die „Dicke“ des ebenen Dehnungsabschnitts ist ziemlich willkürlich und wird normalerweise standardmäßig auf 1,0 eingestellt. Wenn die Belastung des Bauteils als Lauflast durch die Tiefe berechnet wird (N/m, Lbf/inch usw.), dann kann dieser Wert direkt auf das plane Dehnungsnetz angewendet werden. Es ist nützlich, einen Abschnitt auszuwählen, z. B. den einzelnen Tang, und die nominale oder durchschnittliche Spannung in diesem Abschnitt für das gesamte Bauteil zu schätzen. Dies kann als Sanity Check in der Flugzeugdehnungsanalyse verwendet werden. Falsches Laden ist wahrscheinlich die Hauptfehlerursache bei dieser Methode.

Die Ergebnisse der Analyse sind in Abb. 8 und zeigen deutlich die hochbeanspruchten Bereiche um das Schulterfilet herum. Die Spannungen gelten für den mittleren Tiefenbereich des Bauteils (z = 0).

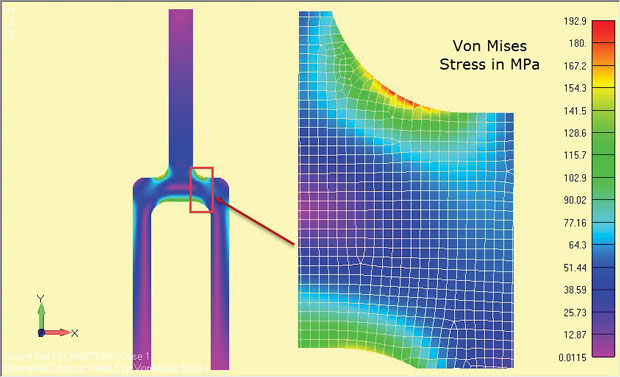Abb. 8: Ebene Dehnungsanalyse Ergebnisse einer tiefen Tang-Komponente.

Die verwendeten Spannungsgrößen hängen vom verwendeten Löser ab. Einige Löser ignorieren die Spannungen in Z-Richtung als sekundär und stellen die Spannungen in der Ebene wieder her. Die Hauptspannungen und Von-Mises-Spannungen beziehen sich dann auf einen 2D-Spannungszustand in der Ebene. Wenn die Spannung in z-Richtung wiederhergestellt wird, sollte sie eindeutig identifiziert werden, damit der 2D-Spannungszustand in der Ebene in der xy-Ebene identifiziert werden kann.

Was genau stellt die Spannung in Z-Richtung dar? Es ist die Spannung, die aufgrund der Erzwingung der Null-Z-Richtungsdehnung entwickelt wird. Die Spannung wirkt, als wären die freien Stirnflächen des prismatischen Abschnitts fixiert. In der Mittelebene einer Tiefschnittkomponente sind dies die komplementären Spannungen, die benötigt werden, um den Dehnungszustand in Null-z-Richtung zu halten. Wenn wir uns in Richtung der freien Oberflächenflächen bewegen, fällt die Z-Spannung auf Null und wird zu einer ebenen Spannungsverteilung (wie in der dicken Bruchmechanikprobe zu sehen).

In vielen Fällen, wie z. B. bei einem Druckzylinder, sind die Stirnflächen mit einer Kappe bedeckt und entwickeln tatsächlich eine axiale Spannung aufgrund axialer Kräfte. Dies ist eine andere Spannung als die induzierte axiale Spannung in der Ebenendehnungsanalyse. Zur Berechnung der axialen Spannungen ist eine Handberechnung erforderlich, oder möglicherweise ein ergänzendes axisymmetrisches Modell für Druckbehälter.

Die einfache Geometrie und Netzkonstruktion eignet sich gut für „Was-wäre-wenn“ -Studien oder formellere Formoptimierungsstudien.

Zum Vergleich wurde eine Halb-Voll-3D-Analyse der tiefen Tang-Komponente durchgeführt und die Ergebnisse sind in Abb. 9. Die Nennspannung über das obere einzelne Tang-Bein ist in beiden Fällen identisch – denken Sie daran, dass dies die Grundlage für jeden Sanity Check ist.

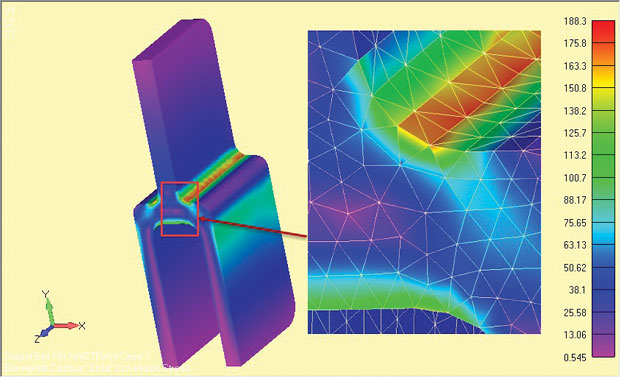Abb. 9: Volle 3D modell der tiefe tang, zeigt stress ergebnisse.

Die lokalen Schulterspannungen sind im Vollmodell um einen kleinen Prozentsatz niedriger. Dies hat drei Gründe. Erstens ist das relativ grobe 3D-Tet-Netz dem sehr feinen lokalen Netz der 2D-Ebene unterlegen. Eine Konvergenzprüfung des 3D-Modells wurde nicht durchgeführt.

Zweitens gibt es eine kleine Änderung in der Geometrie an den freien Oberflächen (+z, -z) im Vergleich zu dem z = 0 Abschnitt aufgrund der Endwölbungen. In diesem Fall ist der Effekt vernachlässigbar, da die Filets von den Schulterbereichen entfernt sind. In vielen Komponenten wird es jedoch lokale Filets geben und Details ausgehen. dadurch wird die Geometrie von einer einfachen xy-Planfläche variiert. Lokale Spannungsschwankungen an freien Stirnflächen müssen möglicherweise mit einem vollständigen 3D-Modell geschätzt oder überprüft werden.

Schließlich gilt die Annahme der Ebenendehnung einer festen z-Einschränkung bei +z, -z Abschnitten nicht für eine endliche Tiefenkomponente. Die z-Spannung wird an den „echten“ freien Flächen auf Null diffundieren. Dieser Effekt ist in Fig. 10, die das 3D-Modell wie es ist und auch als Simulation der ebenen Dehnung z Spannung verwendet.

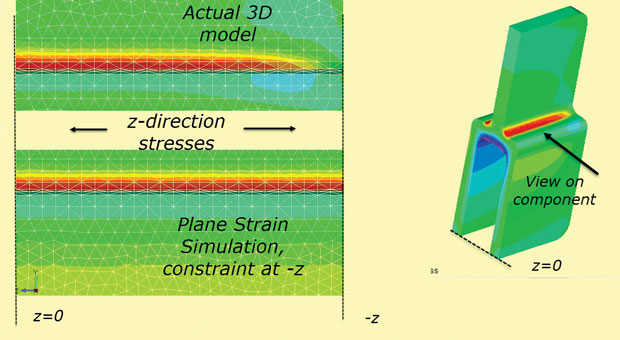Abb. 10: Diffusion der Z-Spannung zur freien Oberfläche.

Schnell und effizient

Planspannungs- und Plandehnungsanalysen sind nützliche 2D-Methoden, die häufig vollständige 3D-Modelle ergänzen können. Nicht alle Merkmale können dargestellt werden, aber mit etwas Einfallsreichtum können Spannungen in Schlüsselbereichen zumindest geschätzt werden. Die Motivation für den Einsatz der Methoden besteht darin, eine schnelle und effiziente Analyse mit einfacher 2D-Geometrie und Netzkonstruktion zu ermöglichen.