WÄRMELEITFÄHIGKEIT

Die Wärmeleitfähigkeit von Festkörpern ist unterschiedlicher Natur, je nachdem, ob sie Leiter sind oder nicht. In Dielektrika ohne freie elektrische Ladungen wird Wärmeenergie durch Phononen übertragen. Die kollektiven Schwingungen von Atomen im Kristallgitter nehmen die Form von Verschiebungswellen an, deren Interferenz Wellenpakete, d. H. Phononen, erzeugt. Die Verschiebungswellen bewirken Dichtefluktuationen, die sich als Variation des Brechungsindex manifestieren können. Wenn die Wellen einen Bereich passieren, in dem der Brechungsindex vom mittleren Volumenwert abweicht, werden die nachfolgenden Verdrängungswellen, die die Energie der thermischen Bewegung tragen, gestreut.

Die Streuung ist umso stärker, je stärker die maximale Abweichung der Atome von ihren mittleren Positionen im Gitter ist, d. H. Je höher das T. Dies erklärt die experimentell festgestellte Tatsache, dass die Wärmeleitfähigkeit von Kristalldielektrika bei relativ hohen Temperaturen abnimmt: λ 1 / T (Abbildung 1).

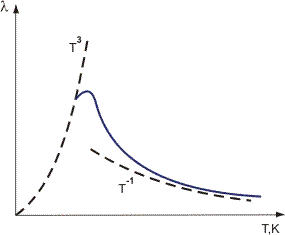
Abbildung 1. Variation der Wärmeleitfähigkeit von Kristalldielektrika mit der Temperatur.

Debye gab einen Einblick in einen peakartigen Charakter der λ(T) -Variation bei niedrigem T im Rahmen quantenmechanischer Konzepte. Er entwickelte eine Dipoltheorie von Dielektrika basierend auf dem Konzept eines Moleküls als starrer Dipol. In diesem Modell führte Debye das Konzept der sogenannten Debye-Temperatur θD ein, die proportional zur maximalen Frequenz atomarer Schwingungen in einem Festkörper ist. Für die meisten Substanzen θD ist entweder niedriger als oder nahe an der Raumtemperatur (eine Ausnahme ist Diamant für die θD = 1850 K und Berrylium für die θD = 1160K).

In der Quantentheorie der Festkörper wird das Kristallgitter als ein mit Phononengas gefülltes Volumen betrachtet, auf das die Ableitung der einfachsten kinetischen Theorie angewendet wird

wobei c die Wärmekapazität eines Dielektrikums ist, die mit der von Phononengas übereinstimmt, v die mittlere Geschwindigkeit der Phononen ungefähr gleich der Schallgeschwindigkeit ist, der mittlere freie Weg der Phononen. Die Existenz eines bestimmten endlichen Wertes von ist das Ergebnis der Phononenstreuung an Phononen, an Defekten des Kristallgitters und insbesondere an Korngrenzen über die gesamte Probe. Die Temperaturabhängigkeit λ(T) wird durch die von und c von der Temperatur bestimmt.

Bei hohen Temperaturen, die die Debye-Temperatur θD wesentlich überschreiten, ist der grundlegende Mechanismus, derbegrenzt, eine Phonon-Phonon-Streuung aufgrund der Anharmonizität von Atomschwingungen in einem Kristall. Der Phonon-Phonon-Mechanismus des Wärmewiderstands ((1 / λ) ist als Wärmewiderstandskoeffizient bekannt) ist nur aufgrund eines Übergangs möglich, der zu einer Verzögerung des Phononenflusses und einer merklichen Änderung des Quasiimpulses führt. Je höher das T, desto höher ist die Wahrscheinlichkeit des Übergangs mit.:(1/ T). Da bei T > θD die Wärmekapazität c mit der Temperatur nur geringfügig ansteigt, ergibt sich λ1/T.

Bei Temperaturen unterhalb der Debye-Temperatur T<<θD wächst die durch die Phonon-Phonon-Streuung bestimmte Länge des mittleren freien Wegesdrastisch an,expθD/T und ist in der Regel auf die Größe eines Kristalls R beschränkt. Nach dem Debye-Gesetz variiert die Wärmekapazität c in diesem Temperaturbereich als c(T/θD)3. Folglich muss bei T → 0 der Wärmeleitfähigkeitskoeffizient λ proportional zu T3 abnehmen. Die Temperatur, für die die Wärmeleitfähigkeit einen Peak aufweist, wird aus ≈ R bestimmt, was üblicherweise T ≤ 0,05θD entspricht.

Diese Theorie berücksichtigt auch das Verhalten des Wärmeleitfähigkeitskoeffizienten für amorphe Substanzen ohne langreichweitige Ordnung, d. H. Die Größe ihrer „Kristalle“ liegt in der Größenordnung der Atomgrößen. Infolgedessen muss die Streuung an den „Grenzen“ dieser Substanzen bei allen T und≈ const . Der Wärmeleitfähigkeitskoeffizient amorpher Substanzen λT3 bei niedrigen Temperaturen und muss im Verhältnis zur Wärmekapazität bei mittleren und hohen Temperaturen leicht ansteigen, T > θD.

All dies liefert eine qualitative Erklärung der Abhängigkeit λ(T) in echten Kristalldielektrika, berücksichtigt jedoch keine Abweichungen vom konstanten Gitter aufgrund atomarer Verunreinigungen anderer Elemente und ihrer eigenen Isotope. Bei einer hohen Temperatur ist der Widerstand, den Verunreinigungen dem Wärmetransport bieten, temperaturunabhängig. Dies ermöglicht es, den Grad der Kristallreinheit aus der Variation seiner Wärmeleitfähigkeit mit der Temperatur abzuschätzen. Dieselbe Tatsache ermöglicht es uns, die Verteilung zwischen glasartiger und kristalliner Substanz im natürlichen Mineral zu bestimmen, wenn das Glas als Verunreinigung in einem Kristall betrachtet wird.

Die Wärmeleitfähigkeit in Metallen hängt von der Bewegung und Wechselwirkung von Stromträgern, d. H. Leitungselektronen, ab. Im Allgemeinen ist der Wärmeleitfähigkeitskoeffizient λ eines Metalls gleich der Summe von Gitter (Phonon) λph und Elektron λe Komponenten, λ = λe + λph; bei gewöhnlichen Temperaturen in der Regel λe >> λph.

Wenn wir eine einfache kinetische Theorie von Gasen auf den Fluss freier Elektronen anwenden und annehmen, dass die Länge ihres freien Weges nicht von der Geschwindigkeit abhängt, dann impliziert die Theorie, dass

wobei e die Elektronenladung, K Boltzrnanns Konstante und σ die elektrische Leitfähigkeit ist. Eine strenge quantenmechanische Theorie bietet eine ähnliche Beziehung,

In beiden Formeln scheint das Verhältnis des Elektronenteils des Wärmeleitfähigkeitskoeffizienten λ zur elektrischen Leitfähigkeit σ in einem weiten Temperaturbereich proportional zur Temperatur nach dem Wiedemann-Franz-Gesetz λ / σ = LT zu sein, wobei L die Lorentzzahl ist. Dieses Gesetz wird verwendet, um λe aus der gemessenen elektrischen Leitfähigkeit zu berechnen. Es wird jedoch bei Temperaturen unter θD verletzt, wenn eine Elektron-Phonon−Wechselwirkung vorherrscht (σ wächst mit abnehmendem T als T−5, während le als T-2 geringfügig variiert).

Die experimentellen Befunde belegen, dass die Wärmeleitfähigkeit von Metallen bei hohen Temperaturen in der Regel eine leicht abnehmende Funktion der Temperatur ist. Aber es gibt viele Ausnahmen. So nimmt die Wärmeleitfähigkeit von Eisen mit der Temperatur stark ab, während Tantal und Niob einen positiven Temperaturkoeffizienten aufweisen.

Von Interesse sind die Versuche, die Wärmeleitfähigkeitskoeffizienten für verschiedene Substanzen für eine einzige charakteristische Temperatur, beispielsweise für den Schmelzpunkt Tm von Feststoffen, zu vergleichen. So hat die statistische Verarbeitung von experimentellen Daten, die von Missenard durchgeführt wurde, gezeigt, dass die Wärmeleitfähigkeit von Metallen am Schmelzpunkt λ(T = Tm) = λm proportional zu λund die Wärmeleitfähigkeit von dielektrischen Kristallen bei T = Tm proportional zu ist, wobei m die Molekülmasse, N die Anzahl der Atome in der chemischen Formel, ρ die Dichte und der Schmelzpunkt Tm in Kelvin ist.

Der Wärmetransport in Halbleitern ist komplexer als in Dielektrika und Metallen, da die Phononen- und Elektronenkomponenten für sie gleichermaßen essentiell sind. Ein weiterer Grund für die Komplexität ist die beträchtliche Wirkung von Verunreinigungen, bipolarer Diffusion und anderen wenig untersuchten Faktoren auf die Wärmeübertragung.

Die Wirkung des Drucks auf die Wärmeleitfähigkeit von Feststoffen kann mit guter Genauigkeit als linear angenommen werden, λ für viele Metalle, die mit p wachsen.

Zur Wirkung der Porosität auf die Wärmeleitfähigkeit von Feststoffen siehe Poröses Medium.