luultavasti yleisimmin käytetty arvo maannosraportissa on maaperän kantavuus. Ilmeinen syy on se, että useimmissa tekstikirjoissa annetuissa perusesimerkeissä käytetään lähes aina kantavuutta pohjamitan laskemiseen. Yksinkertaisuuden ja helppokäyttöisyyden vuoksi tämä menetelmä on edelleen perustavaa laatua oleva maaperän parametri säätiön suunnittelussa. Kuitenkin, että yksinkertaisuus olettaa, että asema käyttäytyy jäykkä elin. Tämä oletus toimii hyvin käytännössä pienten ja yhden sarakkeen jalkineiden kohdalla. Mutta suurten ja monen sarakkeen perustukset, useimmat insinöörit mieluummin joustava analyysi. Joustavan analyysin manuaalinen laskenta voisi olla haastavaa ja lähes kaikissa tapauksissa ohjelmistot, kuten STAAD, SAFE, GT STRUDL jne. käytetään. Nämä tietokoneohjelmat pyytävät kuitenkin usein syötettä, jota kutsutaan ”subgradisen reaktion modulukseksi”. Monet insinöörit eivät tunne tätä termiä ja yrittävät usein verrata sitä kantavuuteen. Koska yhä useammat insinöörit käyttävät ohjelmistoja suunnittelemaan perustuksia, on välttämätöntä, että insinööreillä on perustavanlaatuinen käsitys tästä maaperän parametrista. Onko kantokyvyn ja reaktiomoduulin välillä mitään yhteyttä?
Subgradisen reaktion Modulus (Ks)
tämä termi mitataan ja ilmaistaan kuormituksen intensiteettinä uppouma-yksikköä kohti. Englanninkielisessä yksikköjärjestelmässä se ilmaistaan usein kip/in2/in; SI-järjestelmässä se ilmaistaan kN/m2/m. jotkut ilmaisevat tämän termin kip/in3 (tai kN / m3), mikä voi olla harhaanjohtavaa. Numeerisesti kip / in3 on oikea, mutta ei esitä oikein mitatun arvon fysikaalista merkitystä ja sitä voidaan erehtyä pitämään tiheysyksikkönä tai tilavuusmittauksena.
matemaattisesti alipainekerroin ilmaistaan seuraavasti:
Ks = P / s (Eqn 1)
missä p = kosketuspaineen intensiteetti ja S = maa-aineksen asutus
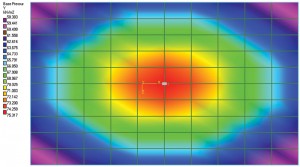
Kuva 1a: Taipumakaavio ja maan paineen ääriviivat.
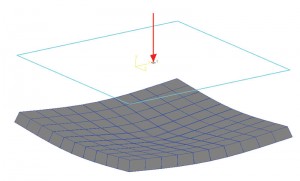
Kuva 1b: maan paineen ääriviivat.
kuten Terzaghi mainitsi, joustavan pohjan kosketuspaineen asianmukainen arviointi voi olla hyvin vaivalloista, joten Ks: n oletetaan pysyvän vakiona koko pohjan ajan. Toisin sanoen paineen ja ratkaisun suhde kaikissa asemapaikoissa pysyy vakiona. Joten Siirtymä kaavio jalalla kuorman keskellä on kupera vaikutus. Kohta keskellä jalansijaa kokee suurimman Siirtymä. Siirtymä pienenee, kun se liikkuu poispäin keskustasta. Kuvassa 1a on yksinkertainen laatta-on-grade perusta. Se mallinnettiin ja analysoitiin STAAD-säätiössä nimellä” Mat”, joka on joustava perusta; maaperä määriteltiin käyttämällä subgradisen reaktion kerrointa. Tässä harjoituksessa käytettiin ohjelmiston oletusarvoa aligradisen reaktion modulukselle. Siirtymä kaavio näyttää disasting vaikutus kuten aiemmin. Kuvassa 1b esitetään maan painekäyrä. On myös selvää, että paineen voimakkuus keskipisteessä on suurin ja pienenee elementtien (tai solmukoordinaattien) siirtyessä pois keskustasta. Voidaan siis olettaa, että paineen voimakkuuden ja ratkaisun suhde on vakio.
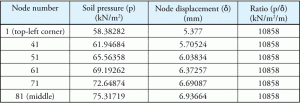
Taulukko 1: Maan paine, solmujen siirtymä ja niiden suhde.
tarkastellaan joitakin lukuja samasta esimerkistä. Maan paine, vastaava uppouma ja suhde on lueteltu taulukossa 1. Pisteet esitetään lävistäjällä, joka havainnollistaa paineen ja siirtymän vaihtelua pisteiden siirtyessä pois keskipisteestä suorakulmaisen kulman kaukaisimpaan pisteeseen. Kuva 2 näyttää pisteitä matto laatta.
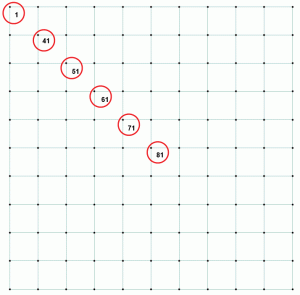
Kuva 2: Valitut pisteet vertailemaan pohjapainetta, taipumaa ja suhdetta.
tämä tuskin on yllätys, sillä määritelmän mukaan subgradisen reaktion modulus (Ks) on vakio koko jalalle ja ohjelma käytti Ks: ää maaomaisuutenaan. On myös tärkeää huomata, että ohjelmiston oletusarvo Ks (10858 kN/m2/m) oli täsmälleen sama kuin taulukossa 1 laskettu vakiosuhde.
Emäspaine laskettiin tukireaktiosta. Voisi ajatella, että myös tukireaktion ja vastaavan siirtymän suhde on vakio. Kuten taulukosta 2 ilmenee, suhdeluvut eivät ole vakio kaikille arvoille. Miten Ks-arvoa käytetään ohjelman sisällä ja miten pohjapaine lasketaan?
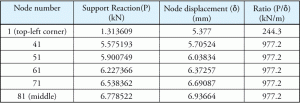
Taulukko 2: Tukireaktio ja syrjäytyminen.
sivujoen pinta-ala
usein oletetaan, kuinka suuri osa laatan pinta-alasta voidaan liittää solmuun tai toisin sanoen kunkin solmun vaikutuksesta laatan pinta-alaan. Se riippuu levyn muodosta. Täydellisen neliön tai suorakaiteen muotoisen levyn kohdalla jokainen solmu vaikuttaa täsmälleen ¼ levyn pinta-alasta (Kuva 3a). Yleistetyssä nelikulmiossa paras käytäntö olisi kuitenkin laskea levyn massan keskipiste ja piirtää sitten viivat kyseisestä keskipisteestä kummankin sivun keskipisteisiin. Kuvassa 3b varjostettu alue kuvaa vastaavan solmun vaikutuspinta-alaa.
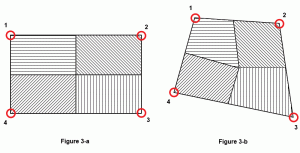
kuva 3: solmun sivujoen alue.
jousivakio
edellä kuvattu sivujoen pinta-alan laskenta on kaupallisen ohjelmiston sisäisesti käyttämä keskeinen menettely lineaarisen jousivakion laskemiseksi. Ohjelma laskee ensin sivujoen pinta-alan jokaiselle solmulle ja kertoo sen jälkeen subgradisen reaktion moduluksen kunkin solmun vastaavalla sivualueen alueella, jotta saadaan lineaarinen jousivakio jokaiseen solmuun.
Kyi = Ks x Tai (Eqn 2)
missä
Kyi on jousivakio ith-solmussa
Tai on ith-solmun vaikutusalue
Ks on subgradisen reaktion modulus
konkreettisessa perustusanalyysissä näiden jousien on oltava määritellään vain puristuskäyttöön, sillä betonin ei oleteta kantavan vetovoimaa. Emäspaine lasketaan kussakin tukisolmussa jakamalla tukireaktio vastaavalla solmun sivualueella. Jos katsomme yllä olevaa esimerkkiä, solmulla 1 on paljon pienempi sivujoen pinta-ala kuin muilla solmuilla. Voidaan myös todeta, että kaikilla muilla solmukohdilla on sama sivujokialue. Tämä selittää taulukon 2, koska se osoittaa suhde solmu 1 on erilainen kuin muut solmut. Kuvassa 4 esitetään sivujoen alue eri solmukohtien osalta. Node 1: n sivujoen pinta-ala on 25% Node 81: stä. Taulukko 3 on taulukoiden 1 ja 2 Laajennus ja osoittaa, kuinka vakiosuhde saavutetaan kaikille solmuille.
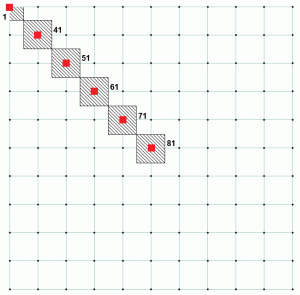
Kuva 4: valittujen solmukohtien Sivujokialue.
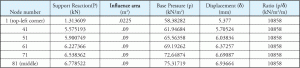
Taulukko 3: reaktio, emäspaine, Siirtymä, Ks-vakio.
sallittu asutus
kantavuus on maanpaineen mitta, jota maa-aines voi turvallisesti kantaa. Toisin sanoen kantavuus on paine, jonka maaperä kestää ennen kuin se pettää. Kaksi tärkeintä maaperän vikaantumisen kriteeriä ovat:
- Shear failure
- suurin sallittu asutus
muun muassa perustusleveys (B) voi vaikuttaa vikaantumiskriteereihin. Yleensä leikkausvirhe hallitsee pienempiä säätiöitä ja selvitysvirhe isompia säätiöitä. Taulukko 4 on tyypillinen esimerkki, joka osoittaa eri meikkivoiteiden ja epäonnistumiskriteerien välisen suhteen.
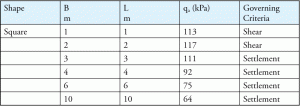
Taulukko 4: lopullinen sallittu kantavuus sallitulle asutukselle = 25 mm ja tietty upotussyvyys.
selvityshäiriön arvioimiseksi oletetaan sallittu selvitysarvo (yleensä 25 mm tai 1 tuumaa). Kun maa laskeutuu yli sallitun arvon, maa pettää. Joten, vaikka kantavuus laskettaessa, sallittu maaperän ratkaisun käytetään ja rakenneinsinöörien pitäisi olla tietoisia, että arvo suunnitellessaan jalusta. Sallittu maa-aineksen selvitysarvo on tyypillisesti olennainen osa mitä tahansa maa-ainesraporttia.
Miksi käyttää Subgradisen reaktion Modulusta
aiemmin todettiin, että joustavan mattoperustuksen suunnittelussa käytetään subgradisen reaktion modulusta maa-aineksen kantavuuden sijaan. Mutta miksi? Vastaus piilee taustalla olevissa oletuksissa siitä, miten säätiö voisi käyttäytyä.
perustukset voivat olla jäykkiä tai taipuisia. Kantavuutta käytetään jäykkien perustusten suunnittelussa, mutta aligradista reaktiota käytetään joustavien perustusten suunnittelussa. Jäykän perustuksen oletus on, että ” subgradisen reaktion P: n jakautumisen pohjan päälle on oltava tasaista, koska jäykkä perusta pysyy tasaisena asettuessaan.”Tarkastellaan yksinkertaisesti tuettua sädettä, joka on ladattu sen keskipisteeseen, kuten kuvassa 5a on esitetty. statiikalla saadaan R1 = P/2 ja R2 = P / 2. Jos sama säde Ladataan eksentrisesti, reaktio voidaan laskea kuvan 5b mukaisesti.
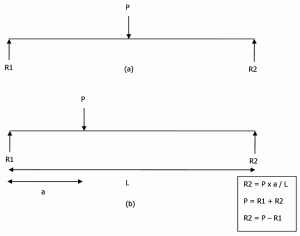
kuva 5: Reaktiot yksinkertaisesti tuetulle säteelle.
samaa konseptia laajennetaan jäykkiin perustuksiin. Mutta lopun tuen sijaan tuetaan koko säätiötä. Oletetaan myös, että betonilaatan suhteellinen jäykkyys on paljon suurempi kuin maan jäykkyys. Niinpä laatan oletetaan pysyvän tasaisena myös kuorman levittämisen jälkeen.
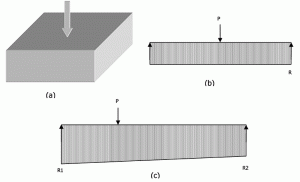
kuva 6: Alaluokkareaktiot eristetyssä asemassa.
Kuvassa 6a näkyy keskelle kuormattu jalusta. Jäykästä leveäsäteen analogiasta p = r x L. Vastaavasti eksentrisesti kuormitettuna reaktio vaihtelee lineaarisesti toisesta päästä toiseen, kuten kuvassa 6c esitetään. yhtälöt 3 ja 4 voidaan ratkaista loppureaktioiden löytämiseksi. Mutta mikään yhtälöistä ei sisällä subgradisen reaktion modulusta (Ks). Niinpä” aligradisen reaktion jakautuminen jäykän pohjan päälle on riippumaton aligradisen puristuvuusasteesta”, jonka päällä se lepää. Kuten monet kirjoittajat ovat päätelleet, jäykkä perusta voidaan turvallisesti suunnitella kantavuus, koska useimmissa tapauksissa tämä menetelmä tuottaa konservatiivisempia tuloksia.
P = 1/2L (R1 + R2) (Eqn 3)
P x A = 1/6B2R1 + 1 / 3B2R2 (Eqn 4)
mutta mattopohja on usein suunniteltu joustavaksi perustaksi, koska se voi olla kooltaan suuri ja siinä voi olla monia kuormituspisteitä ja muita komplekseja, kuten reikiä ja palkkipalkkeja. FEA: n ohjelmistojen laaja saatavuus edistää tätä suuntausta. Mutta toisin kuin jäykät perustukset, joustavalla perustuksella ei voi olla lineaarista subgradista reaktiota. Pikemminkin se riippuu Kokoonpuristuvuus perusta sekä rakenteellinen jäykkyys. Joustava perusta altistuu sisäiselle taipumiselle ja suhteellisille siirtymille kahden laatan välillä. Mitä suurempi rakenteellinen jäykkyys, sitä pienempi suhteellinen Siirtymä. Kirjoittaja testasi tapauksessa erittäin korkea jäykkyys laatta elementtejä, jolloin lähes tasomainen pinta levityksen jälkeen kuorman. Vastaavasti mitä suurempi on subgradisen reaktion modulus, sitä pienempi on painejakauma. Toisin sanoen korkeampi Ks-arvo absorboi enemmän painetta kuormituspisteessä. Näin ollen subgradisen reaktion modulusta, joka on maaperän ratkaisun ja ulkoisen paineen funktio,käytetään joustavaan perustussuunnitteluun.
korrelaatiot
yleisin – ja luultavasti turvallisin – vastaus kysymykseen kantavuuden ja aligradisen reaktion moduluksen välisestä korrelaatiosta on, että korrelaatiota ei ole. Mutta pitäisi olla yksi, koska molemmat ovat mittauksia maaperän kapasiteetin ja mikä tahansa näistä kahdesta muuttujasta voidaan käyttää suunnittelemaan säännöllinen perusta.
jälleen Ks: n määritelmä on paine selvitysyksikköä kohti. Toisin sanoen maaperän kyky kestää painetta tietyn siirtymän. Aiempien keskustelujen perusteella on myös selvää, että kantavuudellakin on sallittu asutus. Siksi on houkuttelevaa päätellä, että subgradisen reaktion modulus on kantavuus asutusyksikköä kohti.
tämä johtopäätös on hyvin samankaltainen kuin Bowlesin esittämä yhtälö.
SI: Ks = 40 (SF)qa kN/m3(Eqn 5)
FPS: Ks = 12 (SF)qa k/ft3 (Eqn 6)
jossa SF = turvallisuustekijä ja qa on sallittu kantavuus.
yhtälöissä 5 ja 6 sallittu kantavuus muutetaan ensin lopulliseksi kantavuudeksi kertomalla se turvallisuuskertoimella. Kirjoittaja oletti yhden tuuman tai 25 mm asutusta. Lopullinen yhtälö on sitten muotoiltu jakamalla lopullinen kantavuus oletetulla ratkaisulla.
yhtälön yleisempi muoto voidaan kirjoittaa näin:
Ks = 
stressi/Siirtymä (Eqn 7)
I = turvallisuustekijä
qa on sallittu kantavuus
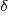on sallittu maa-asutus
nämä yhtälöt osoittavat selvästi, että on käytettävä asianmukaista turvallisuustekijää, ja KS-arvoa voidaan verrata paremmin lopulliseen kantokykyyn kuin sallittuun kantokykyyn. Turvallisuustekijä voi vaihdella projekteista ja geoteknisistä insinööreistä riippuen. Toinen tärkeä tekijä on laskennallisen kantavuuden oletettu sallittu ratkaisu.
vastaavasti on huomattava, että FEA: n analyysin ilmoittamia peruspaineen arvoja ei voida suoraan verrata kantavuuteen. Suurin pohjapaine on kerrottava turvallisuuskertoimella ja verrattava sen jälkeen maaperän sallittuun kantavuuteen.
edellä mainituilla yhtälöillä on kuitenkin rajoituksensa. Niitä voidaan soveltaa alaskirjauksiin, joissa toimitus epäonnistuu, mutta ne eivät voi liittyä alaskirjauksiin, joissa leikkaus epäonnistuu ennen sallitun selvitysrajan saavuttamista. Insinöörien on siis noudatettava varovaisuutta ennen näiden yhtälöiden käyttöä.
johtopäätös
kantokyvyn ja alimoduluksen välinen korrelaatio on parhaimmillaan estimaatti. Sitä voidaan käyttää estimointiin, mutta levykuormitustestillä määritettyä Ks-arvoa on käytettävä aina, jos se on saatavilla tai sitä on pyydettävä aina, kun se on mahdollista. Yllä oleva keskustelu antaa kuitenkin käsityksen näistä arvoista ja auttaa insinöörejä ymmärtämään subgradisen reaktiomoduulin fysikaalisen merkityksen. Ja kuten aina, rakenneinsinöörien tulisi kuulla geoteknisen insinöörin ammattilaista ennen maaperän jäykkyyden ja laakeriarvojen viimeistelyä.▪