ovenavaajan transformaatio (myös ”ovenavaajan reflektointi”) on ortogonaalinen reflektointimuunnos:
- se reflektoi matriisin sarakkeissa olevat vektorit siten, että
- ensimmäisellä vektorilla on kaikki nollat paitsi ensimmäinen alkio
Muunnosmatriisi
Heijastusmuunnos:
ominaisuudet
Kotitalousmatriisit ovat symmetrisiä ja ortogonaalisia: ne ovat heijastusmatriiseja
derivointi
joten meillä on $P = I-2vv^t$:
käytämme tällaisia muunnoksia alkuaineiden nollaamiseen
QR-hajoaminen
kuten LU-hajoamisen tapauksessa, jossa sovellimme sarjaa Gaussin Muunnosmuutoksia, voimme tehdä saman ja suorittaa sarjan Kotitalousmuunnoksia
- joten jos valitsemme $y = \pm e_1$ (jossa $e_1$ on matriisi, jossa 1 on sijalla 1 ja loput ovat nollia)
- , se Nollaa kaikki osat $x$ paitsi ensimmäinen
- siten sopivalla valinnalla $h$ voimme ottaa $a$ ja nollata kaikki Aliviivat elements
- voi tehdä tämän useita kertoja kunkin sarakkeen $A$
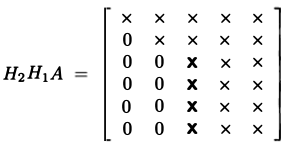
näin voimme suorittaa QR-hajoamisen:
Hessenbergin hajoaminen
sen sijaan, että sitä käytettäisiin matriisin reduktioon Kolmiomaiseksi, voidaan Kotitalousmuunnoksen avulla pelkistää matriisi hessenbergin matriisiksi