
Tervetuloa Steemit ystäväni 1st ever episodi ’ Is it True?’Yritän tässä kirjoitussarjassa paljastaa joitakin melko vaikeasti sulatettavia lausuntoja, kuten sen, josta aion nyt keskustella.
tsekkasin sattumanvaraisesti joitakin blogeja oudoista jutuista. Teen sitä vapaa-ajallani. Lol! Anyways, olin järkyttynyt, kun näin tämän lausunnon blogissa, jossa sanottiin ,”se on matemaattisesti mahdollista, että keskimääräinen paperi, kun taitettu 42 kertaa on tarpeeksi paksu päästä kuuhun.”Luettuani tämän lausunnon, uteliaisuuteni saavutti katon ja halusin vain tarkistaa itse, onko se todella mahdollista.
joten, pitemmittä puheitta, analysoidaan, onko se todella fakta vai vain yksi internetissä satunnaisesti virtaava myytti.
ensinnäkin selvitetään faktat niin, että voidaan edetä pidemmälle laskutoimituksiin.
- tosiasia #1-etäisyys Maasta Kuuhun
- fakta #2-Keskimääräisen paperin paksuus = 0,05 mm
- mukaan nyt meillä on faktat suorassa mennään laskelmiin. Joka kerta, kun paperi on taitettu sen paksuus saa kaksinkertaistui niin tämän mukaan.
- OK. Meillä on numeromme, mutta se on millimetreissä, joten muutetaan tämä valtava luku kilometriksi, jotta saadaan selville, olemmeko jo päässeet kuuhun vai emme?
- Kiitos, että kävitte postauksen läpi. Jos pidit siitä, niin seuraa minua katsomaan enemmän tällaisia.
- myös, älä unohda Upvote ja Resteem
- Steemiläiskaverisi
- Yasir
tosiasia #1-etäisyys Maasta Kuuhun
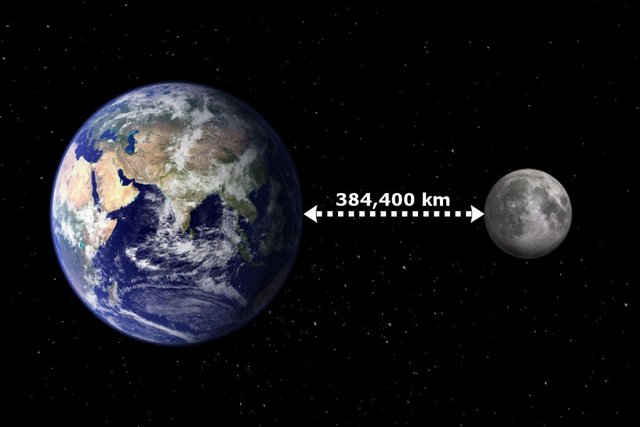
lähteen mukaan
fakta #2-Keskimääräisen paperin paksuus = 0,05 mm

lähteen
mukaan nyt meillä on faktat suorassa mennään laskelmiin. Joka kerta, kun paperi on taitettu sen paksuus saa kaksinkertaistui niin tämän mukaan.
paperin paksuus 1-kertaisen jälkeen = 0, 1 mm
paperin paksuus 2-kertaisen jälkeen = 0, 2 mm
paperin paksuus 3-kertaisen jälkeen = 0.4 mm
paperin paksuus 4-kertaisen jälkeen = 0, 8 mm
paperin paksuus 5-kertaisen jälkeen = 1, 6 mm
paperin paksuus 6-kertaisen jälkeen = 3, 2 mm
paperin paksuus 7-kertaisen jälkeen = 6, 4 mm
paperin paksuus 8-kertaisen jälkeen = 12, 8 mm
paperin paksuus 9-kertaisen jälkeen = 25, 6 mm
paperin paksuus 10-kertaisen jälkeen = 51, 2 mm
paperin paksuus 11-kertaisen jälkeen = 102, 4 mm
paperin paksuus 12-kertaisen jälkeen = 204, 8 mm
paperin paksuus 13-kertaisen jälkeen = 409, 6 mm
paperin paksuus 14-kertaisen jälkeen = 819.2 mm
paperin paksuus 15-kertaisen jälkeen = 1 638, 4 mm
paperin paksuus 16-kertaisen jälkeen = 3 276, 8 mm
paperin paksuus 17-kertaisen jälkeen = 6 553, 6 mm
paperin paksuus 18-kertaisen jälkeen = 13 107, 2 mm
paperin paksuus 19-kertaisen jälkeen = 26,214, 4 mm
paperin paksuus 20-kertaisen jälkeen = 52,428, 8 mm
paperin paksuus 21-kertaisen jälkeen = 104,857, 6 mm
paperin paksuus 22-kertaisen jälkeen = 209,715, 2 mm
paperin paksuus 23-kertaisen jälkeen = 419,430, 4 mm
paperin paksuus 24-kertaisen jälkeen = 838,860.8 mm
paperin paksuus 25-kertaisen jälkeen = 1 677 721, 6 mm
paperin paksuus 26-kertaisen jälkeen = 3 355 443, 2 mm
paperin paksuus 27-kertaisen jälkeen = 6 710 886, 4 mm
paperin paksuus 28-kertaisen jälkeen = 13,421,772, 8 mm
paperin paksuus 29-kertaisen jälkeen = 26,843,545, 6 mm
paperin paksuus 30-kertaisen jälkeen = 53,687,091, 2 mm
paperin paksuus 31-kertaisen jälkeen = 107,374,182, 4 mm
paksuus paperia 32-kertaisen paperin jälkeen = 214,748,364, 8 mm
paperin paksuus 33-kertaisen paperin jälkeen = 429,496,729.6 mm
paperin paksuus 34-kertaisen jälkeen = 858,993,459.2 mm
paperin paksuus 35-kertaisen jälkeen = 1,717,986,918.4 mm
paperin paksuus 36-kertaisen jälkeen = 3,435,973,836.8 mm
paperin paksuus 37-kertaisen jälkeen fold = 6,871,947,673, 6 mm
paperin paksuus 38-kertaisen jälkeen = 13,743,895,347, 2 mm
paperin paksuus 39-kertaisen jälkeen = 27,487,790,694, 4 mm
paperin paksuus 40-kertaisen jälkeen = 54,975,581,388.8 mm
paperin paksuus 41-kertaisen jälkeen = 109,951,162,777.6 mm
paperin paksuus 42-kertaisen jälkeen = 219,902,325,555.2 mm
OK. Meillä on numeromme, mutta se on millimetreissä, joten muutetaan tämä valtava luku kilometriksi, jotta saadaan selville, olemmeko jo päässeet kuuhun vai emme?
tämä on muuntokaappaus
olemme saavuttaneet 219 902,326 kilometrin paksuuden. Aika mahtava oikea! Mutta meiltä puuttuu vielä 165 000 km. jos taittamme paperin vielä kerran, pääsemme Kuun ohi. Voimme siis turvallisesti sanoa, että jos taittamme paperin 43 kertaa, pääsemme varmasti kuuhun.
tiedän, että se on aika mahtava, mutta se on fyysisesti mahdotonta. Miksi? Koska emme voi tehdä tarpeeksi suurta paperia taitettavaksi 43 kertaa. Vaikka löytäisimmekin, emme voi sijoittaa sitä maahan.
Kiitos, että kävitte postauksen läpi. Jos pidit siitä, niin seuraa minua katsomaan enemmän tällaisia.
myös, älä unohda Upvote ja Resteem
Steemiläiskaverisi
Yasir