yksinkertaistaminen FEA mallit: Plane Stress and Plane Strain

toimittajan huomautus: Tony Abbey opettaa live NAFEMS FEA luokat Yhdysvalloissa, Euroopassa ja Aasiassa. Hän myös opettaa nafems e-learning-kursseja maailmanlaajuisesti. Yhteystiedot .yksityiskohtia varten.

edellinen Työpöytätekniikan artikkeli (”Simplify FEA Simulation Models Using Planar Symmetry”) selitti, että tehokkaillakin moderneilla tietokoneilla on usein motivaatiota käyttää yksinkertaistavia tekniikoita rakenteellisessa finiittielementtianalyysissä (FEA). Tässä seurannassa kuvataan, miten kahdella toisiinsa läheisesti liittyvällä menetelmällä voidaan ottaa 2D-viipaleita monimutkaisen rakenteen läpi kiinnostavilla alueilla. Tuloksena olevat FEA-mallit voivat antaa arvokasta tietoa paikallisista rasituksista nopeammin ja tehokkaammin kuin Täysi 3D-malli. Ne eivät kerro koko tarinaa, mutta ovat arvokkaita työkaluja CAE-insinöörille.

näitä kahta FEA-menetelmää kutsutaan tasorasitukseksi ja tasorasitukseksi. Molemmissa käytetään 2D-tasomaisia elementtejä, jotka näyttävät ohutkuorisilta elementeiltä ja jotka on meshattu käyttäen tasomaista pintageometriaa.

Tasojännitysanalyysi

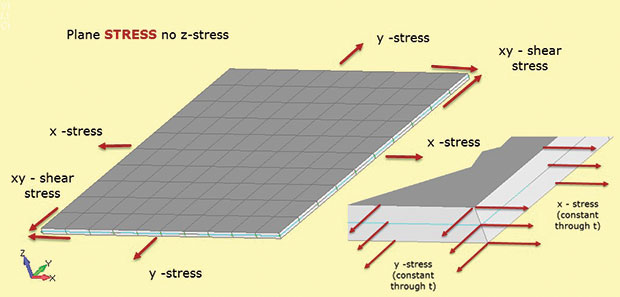
Fig. 1 osoittaa tärkeitä faktoja plane stressianalyysi. Rakenteellisen alueen oletetaan sijaitsevan 2D xy-tasossa, jossa kolmas rakenteellinen ulottuvuus on suhteellisen pieni. Kuvassa tämä on paksuus z-suunnassa. Jännityksiä esiintyy 2D-tasossa Sigma x: nä, Sigma y: nä (suorat jännitykset) ja Sigma xy: nä (tason leikkausjännitys). Jokainen näistä jännityksistä on vakio paksuuden kautta, kuten on esitetty pikkukuvassa. Lisäksi ei voi olla stressiä z suuntaan. Tämä jännitys-venymämateriaalin suhde määritellään 2D-tason jännityselementeissä, joita käytetään tämäntyyppisessä analyysissä.

Kuva. 1: Tasojännitys; stressitilaoletukset.

Z-jännityksen puute on tapa muistaa elementtityyppimerkintä tasojännitys (eli vain tasojännitykset sallitaan). Ei ole myöskään läpi paksuus leikkaus korostaa. Voisimme ladata koneen stressimallin Fig: ssä. 1 kanssa bi-aksiaalinen kuormitus ja laskea sigma x ja sigma y. ei ole sigma z. voimme myös laskea vastaavat In-plane kannat e-x ja e-y. jos sovelletaan leikkaus kuormitus, voimme löytää leikkaus stressi sigma xy ja leikkaus kanta e-xy. Mielenkiintoista, voimme myös laskea läpi paksuus kanta e-z. Tämä ei ole nolla, koska malli on vapaasti ohentua z kun se venyy X ja y. ei ole out-of-plane rajoitus estää tämän. Joissakin ratkaisijat voimme palauttaa läpi paksuus kanta e-z ja käyttää sitä laskea muutos paksuus. (Jos malli on biaksiaalisessa puristuksessa, z-osa saa paksumman). Tätä pidetään yleensä sekundaarisena kantana, eikä sitä välttämättä ole käytettävissä ulostuloon—mutta se on olemassa ja voidaan tarvittaessa laskea käsin.

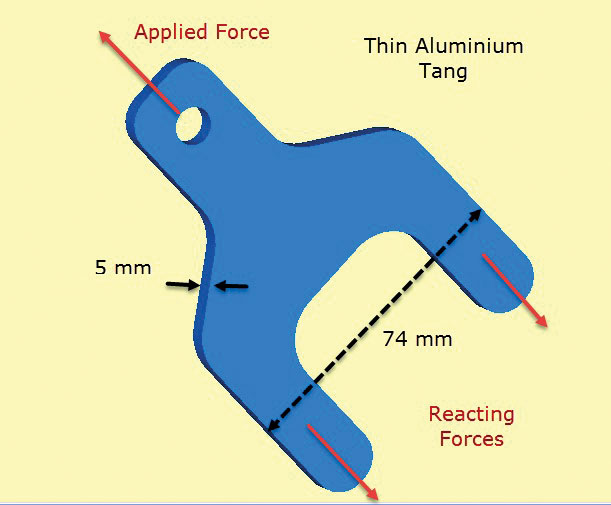
Kuva. 2 näyttää alumiini lug komponentti. Lug työntyy komposiittilevy layup joka on ilmarenkaat sijoitettu ja sidottu yli tangs (tai jalat) ja alavartalon osassa. Tangit siirtävät lugiin kohdistetun kuormituksen komposiittirakenteeseen. Käytännössä laikat porrastettaisiin niin, että sideaines siirtyisi sulavasti sidoksen kautta komposiittiin. Leikkaus siirto komposiitti simuloidaan täällä hajonnut pintavetovoimat ”vetämällä” tangs. Nämä tasapainottavat käytettyä korvakuormaa.

Kuva. 2: Ohutseinäinen alumiini tang siirtää kuorman komposiittirakenteeseen.

keskeinen oletus tässä on, että paksuuden kautta jännitykset ovat nolla ja tasossa jännitykset ovat vakioita komponentin paksuuden kautta. Tämä tarkoittaa, että leikkauskuorman siirron paikallinen yksityiskohta komposiitista tangiin on huonosti mallinnettu. Kuitenkin painopiste tämän analyysin on tarkistaa mitoitus lug ja tang poikkileikkaus selkeä komposiitti, käyttäen In-plane korostaa.

komponentin paksuus on muihin mittoihin verrattuna pieni. Tämä arvo on tulo todellisena paksuutena tasojännityselementin määritelmässä.

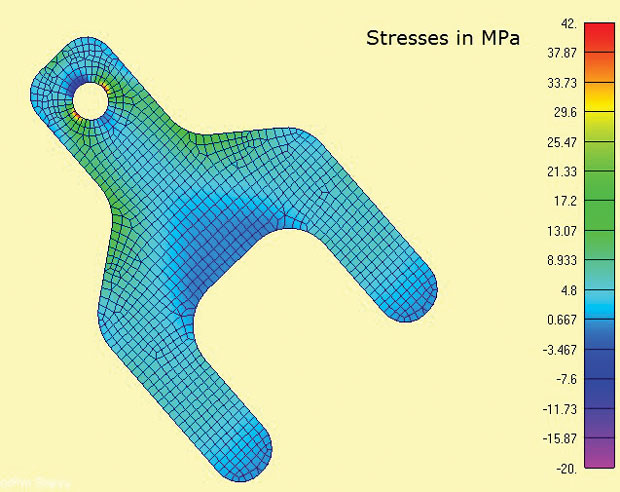
Kuva. 3 esittää FEA-mallin ja lasketut pääjännitykset. Mielenkiintoiset alueet ovat korvakkeiden ja hartiasäteiden ympärillä. Reaalimaailmassa jännitystila jännityspitoisuuksissa olisi 3D ja paksuuden kautta Sigma z-jännitykset ja leikkausjännitykset tasapainottuisivat paikallisesti. Kuitenkin, se on hyvin järkevää tässä olettaa In-plane korostaa hallitsevat. Tämä on sama oletus, joka on implisiittinen useimmissa perinteisissä stressikonsentraatio (kt) – laskelmissa, jotka löytyvät käsikirjoista.

kuva 3: 2D Tasojännityselementit, jotka osoittavat suurimmat pääjännitykset

yksi tasojännitysanalyysin kätevistä piirteistä on se, että se on tiukasti 2D-analyysi, joten vain kolmea vapausastetta (DOF) on rajoitettava (tasonsisäiset käännökset x, y ja kierto z-akselin ympäri). Tämä soveltuu 3-2-1 minimirajoitusmenetelmään tasapainoisella kuormituksella. 2D-tapauksessa tämä degeneroituu 2-1-menetelmäksi. Yksi solmu on DOF x ja y rajoitettu, toinen sopiva ortogonaalinen solmu on DOF x rajoitettu. Näin tangeissa oleva reaktiokuorma voidaan kohdistaa suoraan hajaantuneina tasapainotuskuormina. Olisi vaikea simuloida tätä reunaehto kautta rajoituksia maahan.

läpipaksuus e-z-kanta ja siten tangojen oheneminen voitiin laskea toissijaiseksi vaikutukseksi.

Tasokannan Analyysi

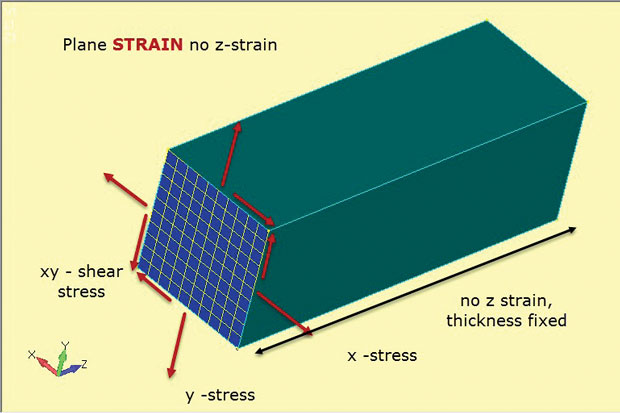
Fig. 4 osoittaa ydin plane kanta menetelmä. Jälleen käytetään 2D-tasoelementtejä, mutta hienovaraisesti eri oletuksilla. Tasossa olevat jännitykset x, y ja xy kehittyvät kuten ennenkin. Kuitenkin tällä kertaa se on out-of-plane, tai läpi paksuus z kanta, joka on asetettu nollaan. Tasokannan analyysi sallii vain tasossa olevat kannat. Tämä toimii hyvin edustaa paksu rakenteita, kuten esitetty. Tämän verran materiaalia on taipumus vakauttaa komponentti ja estää sen venyminen z. tämä tarkoittaa myös sitä, että jatkuva läpi paksuus z jännityksiä kehitetään rakenteeseen. Tämä jännitys-venymämateriaalin suhde määritellään 2D-tason venymäelementeissä, joita käytetään tämäntyyppisessä analyysissä.

Kuva. 4: Plane strain analysis; stress and strain state oletukset.

kuvassa näkyy 2D-tason venymäelementtien suunta leikkausosana tyypillisen syvän komponentin läpi. Oletus on, että jännitystila tässä leikkausosassa monistetaan missä tahansa XY-tason leikkauksessa (z-asemalla) komponentin läpi. Komponentin oletetaan olevan prismaattinen (jonka poikkileikkaus on jatkuva) sen pituudesta alaspäin.

käytännössä käytämme tätä menetelmää, jossa jännitystila vaihtelee hitaasti tasolta toiselle syvässä komponentissa. Syvyyden läpi pitäisi olla tarpeeksi materiaalia stabiloimaan ja poistamaan paksuuskuormitus. Tämä on sama periaate, jota käytetään Fig: ssä esitetyissä murtumissitkeysnäytteissä. 5. Paksun näytteen keskiosassa näkyy vika tasorasituksessa. Vika vapaissa reunoissa ja ohuessa osassa on erilainen tila, enemmänkin tasorasitustila. Tasorasitusmalli FEA olisi määritelmän mukaan hyvä esitys keskilinjan paksun näytteen käyttäytymisestä, mutta ei vapaista reunoista tai ohuesta näytteestä.

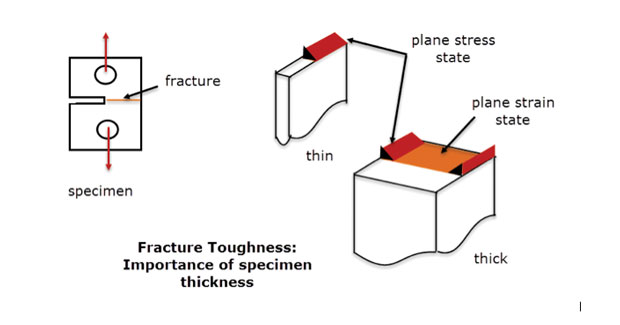Kuva. 5: Murtolujuusnäytteet; ohuet ja paksut osat.

Kuva. 6 näyttää toisen komponentin käytetään komposiitti rakenne, joka muodostaa sidottu yhteinen. Tässä osa on vakio ja riittävän syvä, jotta voimme olettaa, että jännitykset ovat myös vakioita syvyyden kanssa. Vapaan pään pinnoilla (at + z, – z) on erilainen paikallinen jännitystila (itse asiassa tasojännitys, kuten todettiin), mutta tämän analyysin tavoitteena on tarkistaa nettopinnan jännitykset keskilinjalla (z = 0).

2D-tason venymäanalyysi mesh esitetään jaettuna 3D-komponenttiin Kuvassa. 7. Rataosan leikkaus on määritelty asemalla z = 0.

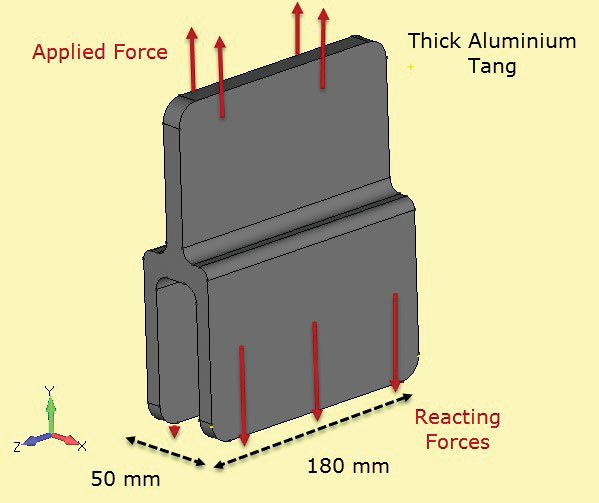kuva 6: Syväperäinen alumiinitango.

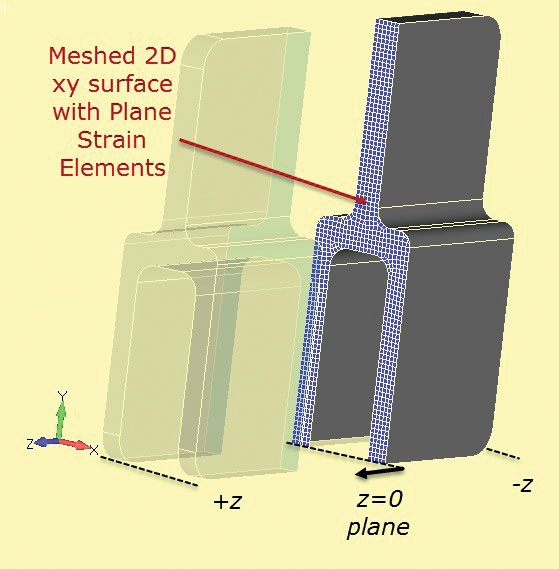Kuva. 7: Osa leikkaa läpi kiinteän osan kehittää 2D taso kanta osassa.

voidaan käyttää erittäin hienoa 2D-tason venymäverkkoa, joka toimii hyvin nopeasti verrattuna täyteen 3D-malliin. 2-1-rajoitusmenetelmää käytetään kuten ennenkin. Kuormausta on harkittava tarkkaan. Tasokantaosan ”paksuus” on melko mielivaltainen, ja se asetetaan yleensä oletusarvoisesti arvoon 1,0. Jos osan kuormitus lasketaan kulkukuormana syvyyden läpi (N/m, Lbf/tuuma jne.) sitten tätä arvoa voidaan käyttää suoraan tasossa kanta mesh. On hyödyllistä valita osa, kuten yksittäinen tangi ja arvioida nimellinen tai keskimääräinen stressi Tässä osassa koko komponentin. Tätä voidaan käyttää järjen tarkistamiseen tasokannatusanalyysissä. Virheellinen lataus on luultavasti tärkein syy virhe tässä menetelmässä.

analyysin tulokset on esitetty kuvassa. 8 ja näytä selvästi kovan rasituksen alueet hartiafileen ympärillä. Jännitykset koskevat komponentin keskisyvyysaluetta (z = 0).

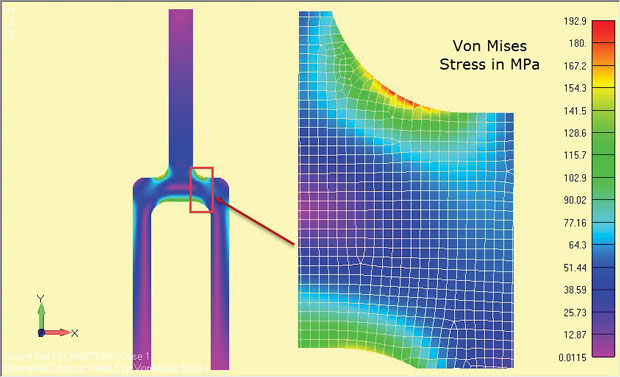Kuva. 8: Tasokantoanalyysin tulokset syvästä tang-komponentista.

käytetyt jännityssuureet riippuvat käytetystä ratkaisijasta. Jotkut ratkaisijat sivuuttaa Z suuntaan korostaa toissijaisena ja palauttaa In-plane korostaa. Pääjännitykset ja von Mises-jännitykset liittyvät sitten 2D-tason jännitystilaan. Jos Z-suuntajännitys otetaan talteen, se on selvästi tunnistettava, jotta X-y-tason 2D-tasojännitystila voidaan tunnistaa.

mitä z-suuntajännitys tarkalleen ottaen edustaa? Se on stressi, joka on kehittynyt nollan z – suunnan rasituksen täytäntöönpanon vuoksi. Stressi toimii ikään kuin prisman osan vapaat päätypinnat olisivat kiinteitä. Syväleikkauskomponentin keskitasolla nämä ovat täydentäviä jännityksiä, joita tarvitaan nollan z-suuntaisen jännitystilan pitämiseksi. Todellisuudessa, kun siirrymme kohti vapaata pintaa, Z-stressi laskee nollaan ja tulee tasorasitusjakauma (kuten nähdään paksu murtuma mekaniikka näyte).

monissa tapauksissa, kuten painesylinterissä, päätypinnat ovat rajattuja ja niihin kehittyy aksiaalisista voimista johtuva aksiaalinen rasitus. Tämä on erilainen jännitys kuin indusoitu aksiaalinen jännitys tasorasitusanalyysissä. Aksiaalijännitysten laskemiseen tarvitaan käsilaskelma tai mahdollisesti paineastioiden täydentävä aksisymmetrinen malli.

geometrian ja mesh-rakenteen helppous sopii hyvin ”mitä jos” – tutkimuksiin tai muodollisempiin muodon optimointitutkimuksiin.

vertailua varten syvästä tang-komponentista tehtiin puolisymmetrinen Täysi 3D-analyysi ja tulokset esitetään kuvassa. 9. Nimellinen jännitys koko ylemmän yhden tang jalka on sama molemmissa tapauksissa-muista tämä on perusta tahansa mielenterveys tarkistaa.

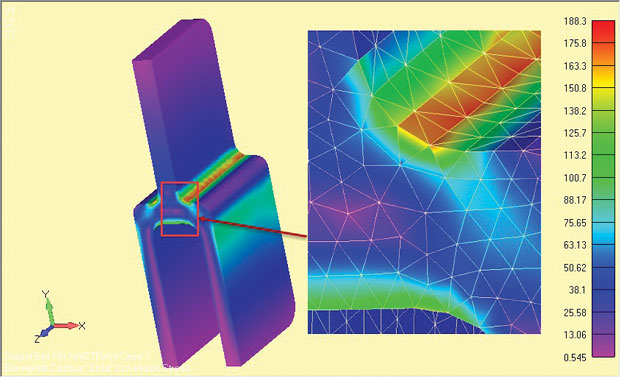Kuva. 9: täydellinen 3d-malli syvästä tangista, joka näyttää stressitulokset.

kokomallissa paikalliset hartiajännitykset ovat pienellä prosentilla pienempiä. Tähän on kolme syytä. Ensinnäkin suhteellisen karkea 3D tet-verkko on huonompi kuin erittäin hieno 2D-tason kanta paikallinen verkko. 3D-mallin konvergenssitarkastusta ei ole tehty.

toiseksi vapaiden pintojen geometriassa (+z, – z) tapahtuu pieni muutos verrattuna Z = 0-osioon päätefileiden vuoksi. Tällöin vaikutus on vähäinen, koska fileet ovat pois lapa-alueilta. Monissa osissa on kuitenkin paikallisia fileitä ja loppuvat yksityiskohdat. joka vaihtelee geometria yksinkertainen xy planar Kasvot. Paikalliset jännitysvaihtelut vapaan pään kasvoilla voidaan joutua arvioimaan tai tarkastamaan täydellä 3D-mallilla.

lopulta tasokannan oletus kiinteästä Z-rajoituksesta pisteessä +z,-z-osuudet ei pidä paikkaansa äärelliselle syvyyskomponentille. Z-stressi hajaantuu nollaan ”todellisilla” vapailla kasvoilla. Tämä vaikutus näkyy kuvassa. 10, joka käyttää 3D-mallia sellaisenaan ja myös simulaationa tasokannan Z-jännityksestä.

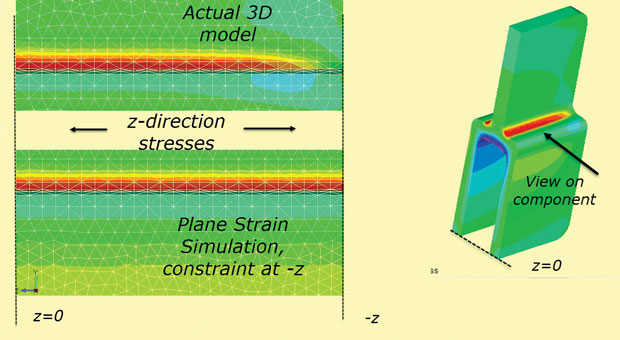Kuva. 10: Z-stressin diffuusio kohti vapaata pintaa.

nopeat ja tehokkaat

Tasorasitus-ja tasorasitusanalyysit ovat hyödyllisiä 2D-menetelmiä, joilla voidaan usein täydentää täysimittaisia 3D-malleja. Kaikkia piirteitä ei voi edustaa, mutta jollain kekseliäisyydellä voidaan ainakin arvioida keskeisten osa-alueiden rasituksia. Menetelmien käytön motiivina on mahdollistaa nopea ja tehokas analysointi helpolla 2D-geometrialla ja mesh-rakenteella.