Algorithme Gourmand avec Exemples: Méthode & Approche Gourmande

Pour comprendre l’approche gourmande, vous devrez avoir une connaissance pratique de la récursivité et de la commutation de contexte. Cela vous aide à comprendre comment tracer le code. Vous pouvez définir le paradigme gourmand en termes de vos propres déclarations nécessaires et suffisantes.

Deux conditions définissent le paradigme gourmand.

• Chaque solution par étapes doit structurer un problème vers sa solution la mieux acceptée.
• Il suffit que la structuration du problème puisse s’arrêter en un nombre fini d’étapes gourmandes.

Avec la suite de la théorisation, décrivons l’histoire associée à l’approche de la recherche gourmande.

Dans ce tutoriel d’algorithme gourmand, vous apprendrez:

• Histoire des Algorithmes Gourmands
• Stratégies et Décisions Gourmandes
• Caractéristiques de l’Approche Gourmande
• Pourquoi utiliser l’Approche Gourmande ?
• Comment résoudre le problème de sélection d’activité
• Architecture de l’approche gourmande
• Inconvénients des algorithmes Gourmands

Histoire des Algorithmes Gourmands

Voici un point de repère important des algorithmes gourmands:

• Des algorithmes gourmands ont été conceptualisés pour de nombreux algorithmes de marche de graphes dans les années 1950.
• Esdger Djikstra a conceptualisé l’algorithme pour générer des arbres couvrant minimaux. Il visait à raccourcir la durée des itinéraires dans la capitale néerlandaise, Amsterdam.
• Au cours de la même décennie, Prim et Kruskal ont réalisé des stratégies d’optimisation basées sur la minimisation des coûts de trajet le long des itinéraires pesés.
• Dans les années 70, des chercheurs américains, Cormen, Rivest et Stein ont proposé une sous-structure récursive de solutions gourmandes dans leur livre classique d’introduction aux algorithmes.
• Le paradigme de recherche gourmande a été enregistré comme un type différent de stratégie d’optimisation dans les enregistrements du NIST en 2005.
• Jusqu’à ce jour, les protocoles qui exécutent le Web, tels que l’open-shortest-path-first (OSPF) et de nombreux autres protocoles de commutation de paquets réseau utilisent la stratégie gourmande pour minimiser le temps passé sur un réseau.

Stratégies et décisions gourmandes

La logique dans sa forme la plus simple a été réduite à « gourmande » ou « non gourmande ». Ces énoncés ont été définis par l’approche adoptée pour avancer dans chaque étape de l’algorithme.

Par exemple, l’algorithme de Djikstra utilisait une stratégie gourmande par étapes identifiant les hôtes sur Internet en calculant une fonction de coût. La valeur renvoyée par la fonction de coût détermine si le chemin suivant est « gourmand » ou « non gourmand ».

En bref, un algorithme cesse d’être gourmand si à n’importe quel stade il fait un pas qui n’est pas localement gourmand. Les problèmes avides s’arrêtent sans autre portée de cupidité.

Caractéristiques de l’approche Gourmande

Les caractéristiques importantes d’un algorithme de méthode Gourmande sont:

• Il existe une liste ordonnée de ressources, avec des attributions de coûts ou de valeur. Celles-ci quantifient les contraintes d’un système.
• Vous prendrez la quantité maximale de ressources pendant le temps qu’une contrainte s’applique.
• Par exemple, dans un problème de planification d’activités, les coûts des ressources sont exprimés en heures et les activités doivent être exécutées en ordre série.

Pourquoi utiliser l’approche gourmande ?

Voici les raisons d’utiliser l’approche gourmande:

• L’approche gourmande comporte quelques compromis, ce qui peut la rendre adaptée à l’optimisation.
• L’une des principales raisons est de parvenir immédiatement à la solution la plus réalisable. Dans le problème de sélection d’activité (expliqué ci-dessous), si d’autres activités peuvent être effectuées avant de terminer l’activité en cours, ces activités peuvent être effectuées dans le même délai.
• Une autre raison est de diviser un problème récursivement en fonction d’une condition, sans avoir besoin de combiner toutes les solutions.
• Dans le problème de sélection d’activité, l’étape « division récursive » est réalisée en balayant une seule fois une liste d’éléments et en considérant certaines activités.

Comment résoudre le problème de sélection d’activité

Dans l’exemple de planification d’activité, il existe une heure de début et de fin pour chaque activité. Chaque activité est indexée par un numéro pour référence. Il existe deux catégories d’activités.

1. activité considérée: est l’Activité, qui est la référence à partir de laquelle la capacité de faire plus d’une Activité restante est analysée.
2. activités restantes : activités à un ou plusieurs indices en avance sur l’activité considérée.

La durée totale donne le coût d’exécution de l’activité. C’est-à-dire (fin-début) nous donne la durée comme le coût d’une activité.

Vous apprendrez que l’étendue gourmande est le nombre d’activités restantes que vous pouvez effectuer au cours d’une activité considérée.

Architecture de l’approche gourmande

ÉTAPE 1)

Scannez la liste des coûts d’activité, en commençant par l’indice 0 comme indice considéré.

ÉTAPE 2)

Lorsque d’autres activités peuvent être terminées au moment où l’activité considérée se termine, commencez à rechercher une ou plusieurs activités restantes.

ÉTAPE 3)

S’il n’y a plus d’activités restantes, l’activité restante actuelle devient la prochaine activité considérée. Répétez les étapes 1 et 2, avec la nouvelle activité considérée. S’il ne reste plus d’activités, passez à l’étape 4.

ÉTAPE 4)

Renvoie l’union des indices considérés. Ce sont les indices d’activité qui seront utilisés pour maximiser le débit.

Explication du Code

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

Explication du code:

1. Fichiers / classes d’en-tête inclus
2. Un nombre maximum d’activités fournies par l’utilisateur.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

Explication du code:

1. L’espace de noms pour les opérations de streaming.
2. Une définition de classe pour l’heure
3. Un horodatage heure.
4. Un constructeur par défaut de TEMPS
5. La variable heures.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

Explication du code:

1. Une définition de classe d’activity
2. Horodatages définissant une durée
3. Tous les horodatages sont initialisés à 0 dans le constructeur par défaut

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

Explication du code:

1. Partie 1 de la définition de la classe du planificateur.
2. L’index considéré est le point de départ de l’analyse du tableau.
3. L’index d’initialisation est utilisé pour attribuer des horodatages aléatoires.
4. Un tableau d’objets d’activité est alloué dynamiquement à l’aide du nouvel opérateur.
5. Le pointeur programmé définit l’emplacement de base actuel de greed.

Scheduler(){ considered_index = 0; scheduled = NULL;......

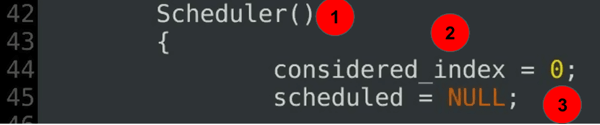
Explication du code:

1. Le constructeur du planificateur – partie 2 de la définition de la classe du planificateur.
2. L’index considéré définit le début actuel de l’analyse en cours.
3. L’étendue gourmande actuelle n’est pas définie au début.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

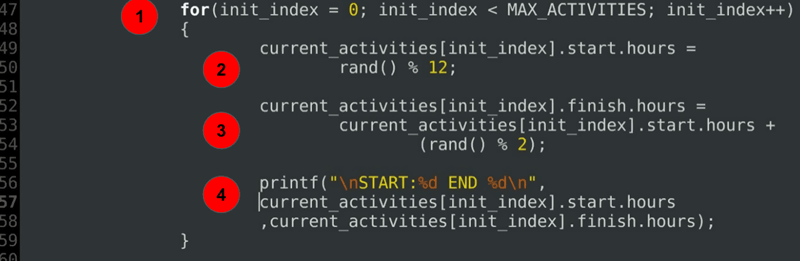
Explication du code:

1. Une boucle for pour initialiser les heures de début et de fin de chacune des activités actuellement programmées.
2. Initialisation de l’heure de début.
3. Initialisation de l’heure de fin toujours après ou exactement à l’heure de début.
4. Une instruction de débogage pour imprimer les durées allouées.

public: Activity * activity_select(int);};

Explication du code:

1. Partie 4 – la dernière partie de la définition de la classe du planificateur.
2. La fonction de sélection d’activité prend un index de point de départ comme base et divise la quête gourmande en sous-problèmes gourmands.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. À l’aide de l’opérateur de résolution de portée (::), la définition de la fonction est fournie.
2. L’index considéré est l’Index appelé par valeur. Le greedy_extent est l’initialisé juste un index après l’index considéré.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

Explication du code:

1. La logique de base – L’étendue gourmande est limitée au nombre d’activités.
2. Les heures de début de l’Activité en cours sont vérifiées comme pouvant être planifiées avant la fin de l’Activité considérée (donnée par l’index considéré).
3. Tant que cela est possible, une instruction de débogage facultative est imprimée.
4. Passez à l’index suivant sur le tableau d’activités

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

Explication du code:

1. Le conditionnel vérifie si toutes les activités ont été couvertes.
2. Sinon, vous pouvez redémarrer votre gourmand avec l’Index considéré comme point courant. Il s’agit d’une étape récursive qui divise goulûment l’énoncé du problème.
3. Si oui, il retourne à l’appelant sans possibilité d’étendre la cupidité.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

Explication du code:

1. La fonction principale utilisée pour appeler le planificateur.
2. Un nouvel ordonnanceur est instancié.
3. La fonction de sélection d’activité, qui renvoie un pointeur de type activité revient à l’appelant une fois la quête gourmande terminée.

Sortie:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

Inconvénients des algorithmes gourmands

Il ne convient pas aux problèmes gourmands où une solution est requise pour chaque sous-problème comme le tri.

Dans de tels problèmes de pratique d’algorithmes gourmands, la méthode gourmande peut être fausse; dans le pire des cas, elle conduit même à une solution non optimale.

Par conséquent, l’inconvénient des algorithmes gourmands est de ne pas savoir ce qui nous attend de l’état cupide actuel.

Voici une représentation de l’inconvénient de la méthode gourmande:

Dans l’analyse gourmande présentée ici sous la forme d’un arbre (valeur plus élevée plus grande cupidité), un état d’algorithme à la valeur: 40, est susceptible de prendre 29 comme valeur suivante. De plus, sa quête se termine à 12. Cela équivaut à une valeur de 41.

Cependant, si l’algorithme a pris un chemin sous-optimal ou adopté une stratégie de conquête. ensuite, 25 seraient suivis de 40, et l’amélioration globale des coûts serait de 65, ce qui est évalué 24 points de plus en tant que décision sous-optimale.

Exemples d’algorithmes gourmands

La plupart des algorithmes de réseau utilisent l’approche gourmande. Voici une liste de quelques exemples d’algorithmes gourmands:

• Algorithme de Spanning Tree Minimal de Prim
• Problème de Vendeur Itinérant
• Coloration de Graphe-Carte
• Algorithme de Spanning Tree Minimal de Kruskal
• Algorithme de Spanning Tree Minimal de Dijkstra
• Couverture de Graphe-Sommet
• Problème de sac à dos
• Problème de planification des tâches

Résumé:

Pour résumer, l’article a défini le paradigme gourmand, a montré comment l’optimisation et la récursivité gourmandes peuvent vous aider à obtenir la meilleure solution jusqu’à un certain point. L’algorithme Gourmand est largement utilisé pour la résolution de problèmes dans de nombreux langages comme l’algorithme gourmand Python, C, C#, PHP, Java, etc. L’exemple de sélection d’activité de l’algorithme Greedy a été décrit comme un problème stratégique qui pourrait atteindre un débit maximal en utilisant l’approche Greedy. Au final, les démérites de l’utilisation de l’approche gourmande ont été expliquées.