INTRODUCTION
Les risques concurrents (CR) sont reconnus comme un cas particulier d’analyse du temps à l’événement depuis le 18ème siècle. De temps en temps, des travaux dans le domaine statistique ou mathématique ont été publiés incorporant de nouveaux développements, y compris la monographie de David et Moeschberger.1 Au fur et à mesure que les données sont devenues plus étendues, claires et précises concernant les différents types de résultats, la CR a refait surface comme un type d’analyse crucial dans l’analyse du délai avant l’événement, nécessaire pour une meilleure compréhension d’une maladie. Le lien entre les résultats mathématiques et le champ appliqué devait être établi. Plusieurs auteurs ont contribué à la compréhension des situations de CR.2, 3 D’autres auteurs ont amélioré et développé des techniques et, dans certains cas, mis à disposition du code informatique prêt à l’emploi pour les statistiques appliquées.4, 5, 6
INTRODUCTION À L’ANALYSE DU TEMPS AVANT L’ÉVÉNEMENT
Dans de nombreuses études, le résultat est observé longitudinalement. De cette façon, chaque sujet de la cohorte est observé pendant un certain temps jusqu’à ce que l’événement se produise. Par exemple, l’événement d’intérêt peut être un décès, une crise cardiaque ou une récidive du cancer. Les objectifs de l’étude peuvent être d’estimer la probabilité de survenue de l’événement ou son association avec des covariables d’intérêt comme le traitement ou les caractéristiques du sujet. L’analyse statistique utilisée est appelée analyse du temps à l’événement ou parfois analyse de survie. La méthode la plus courante pour estimer la probabilité d’un événement est une approche non paramétrique communément appelée méthode Kaplan-Meier7 (KM) ou méthode limite de produit. L’hypothèse principale de l’estimation du KM pour la survie est que les observations censurées connaîtront l’événement si elles sont suivies suffisamment longtemps.
Pour le reste de cet article, les probabilités pour l’événement seront données plutôt que la probabilité pour l’absence d’événement. Par exemple, au lieu de la probabilité de survie, la probabilité de décès sera présentée, qui peut être estimée en utilisant le complément de l’estimateur KM: 1-KM.
INTRODUCTION AUX RISQUES CONCURRENTS
Il n’est pas rare qu’un participant à une étude subisse plus d’un type d’événement. Une situation CR se produit lorsque la survenance d’un type d’événement modifie la capacité d’observer l’événement d’intérêt. Miyasaka et coll.8 a mené une étude sur une cohorte communautaire de patients diagnostiqués avec une fibrillation auriculaire entre 1986 et 2000 dans le comté d’Olmsted, Minnesota, États-Unis. Le résultat principal était l’apparition de la démence. Le suivi médian était de 4,6 ans. Les autres types d’événements étaient les accidents vasculaires cérébraux et la mort. Sur les 2 837 personnes atteintes de fibrillation auriculaire, 299 étaient atteintes de démence et 1 638 étaient décédées au moment de l’analyse. Les chiffres avec AVC ne sont pas signalés et sont censurés dans l’analyse. La conclusion de l’étude était que l’incidence de la démence chez les personnes atteintes de fibrillation auriculaire est fréquente (10,5% à 5 ans en utilisant la méthode KM). La survenue d’un accident vasculaire cérébral avant la démence n’affecte pas l’observation de la démence et il ne s’agit donc pas d’un événement CR. Pour des raisons d’argumentation, nous ignorons le fait que plusieurs accidents vasculaires cérébraux peuvent provoquer une démence. En revanche, un décès sans démence préalable rend l’observation de la démence impossible. Par conséquent, un décès sans démence est un événement CR pour le point final de la démence. De plus, une blessure grave à la tête pourrait être considérée comme un événement de CR, car les changements de comportement du patient pourraient rendre le diagnostic de démence impossible.
Une situation de CR plus subtile se produit dans l’étude menée par Whalley et al.9 de l’importance de l’échocardiographie. Cette cohorte de 228 patients symptomatiques âgés a subi une échocardiographie et a été suivie pour une hospitalisation cardiovasculaire ou un décès cardiovasculaire. L’hypothèse était que les caractéristiques de l’échocardiographie prédisent les événements cardiovasculaires. Le résultat principal a été défini comme la mesure composite incluant la mort cardiovasculaire et/ou l’hospitalisation. Pour ce type de résultat, un décès pour des causes autres que les maladies cardiovasculaires est un événement de CR et, en tant que tel, un patient ne risque plus d’avoir l’un des événements d’intérêt.
Un essai randomisé à 3 bras, en double aveugle, a été mené dans 931 centres et 24 pays pour tester l’effet du valsartan vs valsartan + captopril vs captopril seul (VALIANT) 10 sur la mortalité toutes causes confondues. Au total, 14 703 patients post-infarctus du myocarde présentant un dysfonctionnement du ventricule gauche et / ou une insuffisance cardiaque ont accumulé 1: 1: 1 dans les 3 bras. Étant donné que tout décès a été considéré comme un événement, ce type de résultat n’a pas de CR. L’étude a soutenu l’hypothèse selon laquelle la survie dans les 3 bras était différente. Cependant, des saignements gastro-intestinaux (GI) ont été identifiés comme un effet secondaire grave dans les 3 bras. Moukarbel et coll.11 a étudié les facteurs possibles qui pourraient prédire les saignements gastro-intestinaux. Pour ce critère d’évaluation, la mort sans saignement gastro-intestinal est un CR clair.
Un nombre croissant de chercheurs reconnaissent la présence de CR et la nécessité d’appliquer des techniques appropriées. Une cohorte de 972 patients atteints du syndrome coronarien aigu d’élévation du segment non ST entre 2001 et 2005 a été étudiée par Núñez et al.12 L’un des objectifs de l’étude était de trouver des facteurs associés à la réhospitalisation de l’insuffisance cardiaque aiguë. Parmi les facteurs étudiés figuraient le diabète, des antécédents de cardiopathie ischémique, une insuffisance rénale chronique, des antécédents de tabagisme et des antécédents de traitement. Les auteurs ont reconnu la possibilité de CR comme la mort avant la réhospitalisation et ont correctement appliqué des techniques spécifiques pour tenir compte de la situation de CR.
Melberg et al.13 a étudié une cohorte de 1234 patients atteints de maladie coronarienne symptomatique ayant reçu 2 types de traitements: pontage coronarien (n = 594) ou intervention coronarienne percutanée (n = 640). Sur les 301 décès observés au cours du suivi, 42,5% étaient des décès cardiaques et le reste des décès non cardiaques. Les auteurs présentent des résultats pour la mortalité toutes causes confondues ainsi que pour la mortalité cardiaque et la mortalité non cardiaque. Ils soulignent que le pourcentage de mortalité toutes causes confondues est la somme du pourcentage de mortalité cardiaque et non cardiaque correctement estimé en tenant compte du CR. Les auteurs soulignent l’importance d’analyser chacun des événements d’intérêt plutôt que de les combiner en une mortalité globale. Ce sujet est également exposé à un niveau plus général par Mell et Jeong.14
Comme on peut le supposer à partir des exemples ci-dessus, la question principale en présence de CR est de savoir s’il faut ignorer le CR et censurer les observations impliquant CR ou tenir compte de CR. Lorsque les CR sont ignorés et que les observations des CR sont censurées, l’analyse se réduit à un scénario de délai « habituel ». En raison de la familiarité de ce type d’analyse et de la disponibilité des logiciels, de nombreux chercheurs ont recours à cette approche, comme on le voit dans les exemples précédents. Cependant, il est unanimement convenu non seulement parmi les statistiques2,15, 16, 17, 18 que l’estimation de la probabilité d’événement dans ce cas surestime la probabilité réelle. La prochaine question naturelle est de savoir si la modélisation peut être effectuée dans ces limites (ignorer / censurer CR). C’est plus ambigu et plus difficile à saisir. Bien qu’une telle analyse ne soit pas dénuée de valeur, son interprétation est presque toujours semée d’embûches. La principale exigence est que l’événement CR (dont les observations ont été censurées et mélangées aux véritables observations censurées) doit être indépendant de l’événement d’intérêt. Si tel est le cas, les résultats pourraient être interprétés comme l’effet de covariables lorsque les événements CR n’existaient pas. Cependant, cette hypothèse ne peut généralement pas être formulée et ne peut être vérifiée ou testée. En conclusion, chaque fois que les observations CR sont censurées, l’estimation de la probabilité d’événement est incorrecte et l’interprétation de l’effet des covariables n’est pas claire en raison du manque de connaissance de l’indépendance entre l’événement d’intérêt et l’événement CR.
Lorsque l’analyse est effectuée en tenant compte de CR (et codée distinctement de l’événement d’intérêt ou de la censure), la probabilité est correctement estimée et la modélisation a une interprétation simple. Il n’y a pas de présomption d’indépendance pour entraver l’interprétation. Le coefficient d’une covariable ainsi estimé représente l’effet de cette covariable sur les probabilités observées.
Plusieurs auteurs19,20 ont tenté de comparer les deux approches en termes de puissance des tests à l’aide de simulations. Cependant, le chercheur doit être conscient que le principal problème réside dans l’interprétation des résultats. Quelle que soit la puissance des tests, l’analyse doit répondre à la question de l’étude.
ESTIMATION DE LA PROBABILITÉ D’UN ÉVÉNEMENT
Il est courant d’appliquer la méthode KM pour estimer la probabilité d’un événement. La formule typique pour l’estimation du KM est la suivante
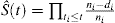
, où t1t2t3ni représente le nombre de patients à risque au moment ti et di est le nombre d’événements au moment ti.
Cette formule peut être transformée par manipulation algébrique pour exprimer la probabilité d’événement comme:
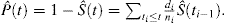
En présence de CR, il existe au moins 2 types d’événements: l’événement d’intérêt, identifié par l’indice e, et l’événement à risque concurrent, identifié par l’indice c. Kalbfleisch et Prentice ont introduit la formule pour la probabilité d’un événement d’intérêt en présence de CR:
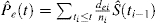
Il est intéressant de noter la relation entre (1) et (2). Puisque di est le nombre de tous les événements à ti, il peut être conçu comme la somme du nombre d’événements d’intérêt dei et du nombre d’événements CR dci à l’instant ti. En tant que telle, la probabilité de tout type d’événement peut être décomposée comme suit:
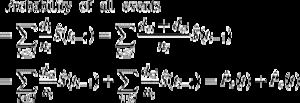
Ainsi, la probabilité de tous les événements peut être décomposée dans les probabilités pour chaque type d’événement.
Si le 1-KM est utilisé pour calculer la probabilité d’un événement d’intérêt en présence de CR, la survie de tous les événements de la formule (2) est remplacée par l’estimation du KM basée uniquement sur les événements d’intérêt. Cela biaisera les résultats, comme cela sera montré plus loin. L’hypothèse principale pour l’utilisation de la méthode KM est que les patients censurés, s’ils sont suivis assez longtemps, finiront par vivre l’événement. Cependant, lorsque la méthode de la KM est utilisée en présence de CR, les patients éprouvant des types d’événements autres que l’événement d’intérêt sont généralement censurés, même s’ils ne sont plus à risque pour l’événement d’intérêt. De plus, la belle décomposition vue en (3) ne peut être effectuée pour la formule 1 KM.
Dans des situations appliquées, il est possible qu’il existe plusieurs autres types d’événements qui ne présentent pas d’intérêt. Dans ce cas, tous peuvent être regroupés sous l’égide d’événements CR.
On montrera à travers un exemple que l’utilisation de la méthode KM n’est pas appropriée en présence de CR.
Description de l’exemple
Un ensemble de données recueillies pour étudier les effets tardifs du traitement du lymphome de Hodgkin sera utilisé à titre d’illustration. Le résultat principal est l’hospitalisation pour maladie cardiaque. Le lymphome de Hodgkin est un type de cancer qui apparaît principalement chez les jeunes adultes. À ses débuts, il est presque guérissable, avec une survie globale de 70% sur 10 ans. Ainsi, une cohorte de ces patients est idéale pour étudier les effets secondaires à long terme du traitement. L’ensemble de données utilisé ici est un sous-ensemble d’une cohorte plus importante qui sera rapportée ailleurs. Les données sont également modifiées pour servir nos objectifs. Par exemple, pour simplifier, nous n’avons conservé dans les données que les patients ayant subi une chimiothérapie ou une radiothérapie, à l’exclusion de ceux ayant reçu un traitement combiné. Pour augmenter le taux de CR (décès sans hospitalisation cardiaque), nous avons inclus des patients de tous les stades. Certaines dates de suivi et de décès ont été imputées. En raison des modifications apportées aux données, aucune conclusion clinique ne peut être tirée de cette analyse. Les données présentées ici font référence à 689 enregistrements avec 93 hospitalisations cardiaques et 467 décès.
Les taux d’hospitalisation cardiaque et de décès sans événement cardiaque seront calculés à la fois en utilisant la méthode KM (1) et la fonction d’incidence cumulée (CIF) introduite à cet effet par Kalbfleisch et Prentice21 (2).
La Méthode de Kaplan-Meier Appliquée à une Situation à Risques Concurrents Surestime le Taux réel de l’Événement
La Figure 1 présente les estimations CIF et 1 KM pour l’hospitalisation cardiaque du groupe traité uniquement par chimiothérapie. La ligne brisée correspondant aux estimations de 1 KM se trouve au-dessus de la ligne continue représentant les estimations du CIF. On peut montrer mathématiquement que 1 KM surestime toujours la probabilité d’événement. Une idée fausse commune est que les estimations de 1 KM sont correctes si les deux événements sont indépendants. L’indépendance entre les événements est au mieux toujours discutable, mais même lorsque les données sont simulées comme des événements indépendants, la différence entre les estimations CIF et le 1 KM existe. La taille de la différence dépend du nombre d’événements, à la fois pour les événements d’intérêt et les événements CR. Dans Miyasaka et coll., 8 l’incidence de la démence à 5 ans en utilisant la méthode KM était de 10,5%. Le nombre de CR (décès) représentait environ les trois quarts du nombre total d’événements, ce qui suggère que leur estimation pourrait être beaucoup plus grande que ce qui est observé.
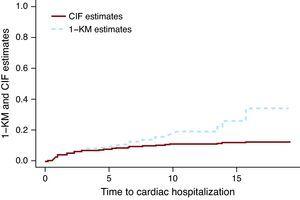
Figure 1. Fonction d’incidence cumulative vs estimations de 1-Kaplan-Meier.. CIF, fonction d’incidence cumulative; KM, Kaplan-Meier.
La Fonction d’Incidence Cumulée Divise la Probabilité de Tout Événement (Hospitalisation Cardiaque ou Décès) En Probabilités Constitutives
Ceci est algébriquement prouvé dans (3). Cependant, pour une compréhension plus approfondie de son fonctionnement, il sera montré graphiquement qu’à partir de la probabilité de tous les événements, une partie participe au CIF pour un événement et l’autre au CIF pour l’autre événement. La figure 2A montre la probabilité de tout événement: hospitalisation cardiaque ou décès sans hospitalisation cardiaque. La figure 2B ne contient que la courbe comprise entre 10,7 et 10.85 ans, de sorte que les marches sont visibles. Sur chaque pas, il y a un cercle. Les cercles ouverts apparaissent sur les étapes dans lesquelles un décès a été observé tandis que les cercles solides sont sur les étapes dans lesquelles une hospitalisation cardiaque s’est produite. Les étapes à cercles pleins participent au CIF pour l’hospitalisation cardiaque dans le panel C et celles à cercles ouverts participent à la courbe de décès sur la Figure 2D. Ainsi, chaque étape contribuera à la probabilité de l’événement qui le provoque. De cette façon, à tout moment, la probabilité de tous les événements est la somme de la probabilité de l’événement d’intérêt et de la probabilité de CR. Notez que les 3 derniers panneaux (Figure 2B-D) montrent la même fenêtre de temps et ont la même longueur pour l’axe des ordonnées de sorte que la taille des marches peut être comparée entre eux. Le tableau 1 montre ces probabilités à 1, 2, 3, 4 et 5 ans.
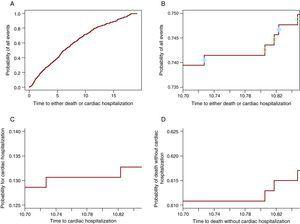
Figure 2. La partition de la probabilité de tous les événements en probabilités constitutives. A. La probabilité d’hospitalisation cardiaque ou de décès. B. La probabilité d’hospitalisation cardiaque ou de décès uniquement pour la fenêtre de temps 10,70-10,85 ans. Les cercles pleins indiquent l’hospitalisation cardiaque et les cercles ouverts représentent les décès sans hospitalisation cardiaque. C. La probabilité d’hospitalisation cardiaque dans la fenêtre de temps 10,70 -10,85 ans. D. La probabilité de décès sans hospitalisation cardiaque dans la fenêtre de temps 10,70-10,85.
Tableau 1. La Probabilité de Tout Événement Est la Somme des Probabilités Constitutives.
| Année de déclaration | Probabilité d’hospitalisation cardiaque | Probabilité de décès | Probabilité d’hospitalisation cardiaque ou de décès |
| 1 | 0.038 | 0.054 | 0.092 |
| 2 | 0.054 | 0.139 | 0.193 |
| 3 | 0.072 | 0.193 | 0.265 |
| 4 | 0.076 | 0.25 | 0.327 |
| 5 | 0.087 | 0.305 | 0.392 |
Parce que le 1 KM surestime la probabilité d’un événement, si nous essayions d’ajouter les estimations du 1 KM pour une hospitalisation cardiaque au 1 KM pour un décès, nous obtiendrions un taux beaucoup plus élevé que la probabilité de tout événement. Dans certains cas, le nombre obtenu est même supérieur à 1, ce qui prouve qu’en présence de CR, les estimations de 1 KM ne sont même pas des probabilités.
La Méthode de la Fonction d’Incidence Cumulée Estime-t-Elle en Effet la Probabilité Correcte d’Événement?
A cet effet, un ensemble de données de 500 enregistrements a été simulé de telle sorte qu’il n’y ait pas de censure avant 5 ans et qu’il y ait 2 types d’événements: le type 1 et 2. Le tableau 2 indique pour chaque type d’événement le nombre observé jusqu’à ce moment, le taux brut et l’estimation CAF, qui sont exactement égaux. L’égalité ne se produit que lorsqu’il n’y a pas d’observations censurées jusqu’à ce moment-là. En présence d’observations censurées au cours des années déclarées, l’égalité ne tient pas et la bonne façon d’estimer la probabilité est le CAF et non le taux brut.
Tableau 2. La Probabilité des Deux Types d’Événement Lorsqu’Il N’Y A Pas D’Observations Censurées Jusqu’À 5 Ans.
CIF, fonction d’incidence cumulative.
En conclusion, pour calculer la probabilité d’événement en présence de CR, il faut utiliser la méthode introduite par Kalbfleisch et Prentice, communément appelée courbe d’incidence cumulative.
MODÉLISATION
Un aspect important d’une analyse consiste à tester l’association entre une covariable et l’événement d’intérêt, soit seul, soit en l’ajustant pour d’autres facteurs. En l’absence de CR, cela se fait systématiquement en utilisant le modèle des dangers proportionnels de Cox (PH de Cox).22
En présence de CR, le modèle de Cox PH n’a pas d’interprétation simple. Si le temps des 2 types d’événements peut être considéré comme indépendant, les résultats peuvent être interprétés comme montrant l’effet dans la situation où CR n’existe pas. Cependant, l’hypothèse de l’indépendance peut rarement être faite ou testée et, par conséquent, les résultats du modèle de Cox PH ne sont généralement pas interprétables.
Modèle Fin et Gris
Fin et Gris6 (F & G) a modifié le modèle de PH de Cox pour tenir compte de la présence de CR. La modification technique consiste à maintenir les observations du CR dans l’ensemble des risques avec un poids décroissant. De cette façon, la méthode F&G modélise les risques de sous-distribution. L’effet estimé à l’aide du modèle F & G montre les différences actuelles et réelles entre les groupes de traitement en termes de rapports de risques de sous-distribution. L’hypothèse de la proportionnalité des dangers est toujours une exigence, mais elle fait bien sûr référence aux dangers de sous-distribution. Le modèle F &G peut prendre en compte des coefficients dépendant du temps pour modéliser la non-proportionnalité des dangers. Ce modèle peut être appliqué à la fois à l’événement d’intérêt (hospitalisation cardiaque) ou au CR (décès).
Les modèles Cox PH et F & G ont été appliqués à l’ensemble de données sur le lymphome de Hodgkin pour tester l’option de traitement de la chimiothérapie par rapport à la radiothérapie. Pour cet exemple (Tableau 3), les résultats des modèles Cox PH et F&G diffèrent sensiblement (2 premières lignes). Comme mentionné ci-dessus, les résultats de Cox PH ne sont pas interprétables et ne peuvent pas être utilisés. La deuxième rangée montre qu’il y a plus d’hospitalisations cardiaques dans le groupe des radiations et la troisième rangée montre plus de décès dans le groupe des chimiothérapies. La figure 3 montre ces résultats graphiquement. Il est possible que la chimiothérapie seule ait été administrée à des patients présentant une maladie plus avancée et que ces patients aient également plus de chances de mourir de leur cancer. D’autre part, le rayonnement seul a probablement été administré à des patients à un stade précoce qui vivaient plus longtemps après le diagnostic de lymphome de Hodgkin. Ces patients avaient plus de chance de développer des effets secondaires tardifs comme une maladie cardiaque.
Tableau 3. L’Effet du Traitement Lorsque des Risques Proportionnels de Cox et des Modèles Fins et Gris Sont Utilisés.
CI, intervalle de confiance; PH de Cox, Modèle de risques proportionnels de Cox; F & G, Modèle fin et gris; HR, rapport de risque.
Les rapports de risque montrent l’augmentation des risques pour le groupe radiologique par rapport au groupe chimiothérapeutique.
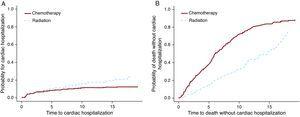
Figure 3. L’effet du traitement en cas d’hospitalisation cardiaque et de décès.
Comme on peut le voir dans cet exemple, l’interprétation des résultats est un travail de collaboration entre le statisticien et le clinicien qui a une connaissance approfondie de la maladie.
La présence de CR complique à la fois l’analyse et l’interprétation des données. Pour permettre au lecteur d’interpréter correctement les résultats, les auteurs doivent inclure des détails sur les événements observés même s’ils peuvent ne pas sembler importants à première vue. Par conséquent, lorsque le critère d’évaluation est observé au fil du temps, les auteurs doivent inclure l’événement d’intérêt, s’il existe une possibilité de CR, le nombre de patients éprouvant l’un de ces types d’événements et la durée du suivi. En présence de CR, il est informatif d’inclure l’analyse pour l’événement d’intérêt ainsi que l’analyse pour CR, car elles se complètent et pourraient aider à interpréter les résultats.
L’Approche Logistique
Supposons d’abord que nous sommes dans le cadre de no CR. Lorsque le résultat devrait se produire dans un court intervalle (par exemple, 1 an), l’outil de choix pour de nombreux chercheurs est la régression logistique. Ceci est approprié si chaque individu de la cohorte a le suivi minimum, dans ce cas 1 an. En fait, l’estimation de la mortalité à 1 an coïncidera avec l’estimation de 1 KM. Le seuil temporel doit être le même pour chaque individu de la cohorte. Par conséquent, si le résultat d’intérêt est une mortalité de 1 an et qu’un individu de la cohorte décède à 1 an et 2 jours, cette personne doit être considérée comme « aucun événement à 1 an. »Cela peut réduire le nombre d’événements, ce qui se traduit par une analyse moins qu’idéale lorsque de nombreux événements observés se produisent après le point de coupure.
Les mêmes règles de base s’appliquent lorsque des CR sont présents. Toutes les personnes de la cohorte doivent avoir le suivi minimum choisi comme point limite de temps, et ce point limite doit s’appliquer à toutes les personnes de la cohorte. Les coefficients et les valeurs p donneront en général le même message mais ne seront pas exactement les mêmes pour la régression logistique par rapport au modèle F &G. Tout d’abord, dans la régression logistique, le coefficient représente le log du rapport de cotes, tandis que dans le modèle F & G, il est le log du rapport des sous-distributions de risques. De plus, dans l’analyse logistique, tous les événements ne sont pas utilisés et bien sûr, un modèle différent est utilisé.
CALCUL DE LA PUISSANCE
Lorsque la mesure est en temps d’événement, le calcul de la puissance comporte deux étapes. La première étape consiste à calculer le nombre d’événements nécessaires pour détecter une taille d’effet spécifique. Ensuite, le nombre de patients nécessaires pour observer ce nombre d’événements est calculé. Il a été souligné dans les sections précédentes que lorsque des CR sont présents, il n’est pas possible d’observer tous les événements d’intérêt en raison de l’apparition de CR. Étant donné que le nombre d’événements est central dans le calcul de la puissance, des précautions supplémentaires doivent être prises pour que les CR soient pris en compte. Si les CR ne sont pas pris en compte, l’étude sera sous-alimentée et donc probablement infructueuse (et peut-être contraire à l’éthique).
LOGICIEL
Le logiciel R open source sur le site CRAN (the Comprehensive R Archive Network) (http://cran.r-project.org/) propose un package (cmprsk) implémenté par Dr. Robert Gray contenant les outils nécessaires pour une analyse complète de la comptabilité du CR. Ainsi, on pourrait obtenir des diagrammes de probabilité observés pour l’événement d’intérêt et une valeur p basée sur le test de Gray, qui est un test logrank modifié pour la situation CR. Dans le package, il existe également une fonction de modélisation utilisant l’approche F& G. Luca Scruca a amélioré la livraison en sortie de la fonction de modélisation pour une lecture plus facile en incorporant dans le package une fonction de type résumé. Le modèle a la possibilité de vérifier la proportionnalité des dangers, et des termes pour les coefficients dépendants du temps peuvent être inclus. Le code ne peut pas prendre en charge la troncature gauche ou les données de cluster. La troncature de gauche serait utile pour l’analyse des événements multiples / récurrents par patient ou pour l’analyse de la cohorte de cas. Un code pour les études de cohorte de cas a été élaboré (Pintilie et al.23) et peut être obtenu auprès des auteurs. Zhou et coll.24 a étendu le modèle F & G pour s’adapter aux données stratifiées et aura également une version pour les données de cluster. À ce stade, le code peut être obtenu des auteurs pour les deux cas, mais il est probable qu’il sera soumis au CRAN.
STATA 11 a récemment implémenté le modèle F &G. Il faut savoir que les graphes obtenus à l’aide de STATA sont des graphes prédictifs plutôt que des graphes de probabilité observés. Il y a deux mises en garde lorsque des courbes prédites sont utilisées: a) les lignes apparaîtront toujours comme si la proportionnalité des dangers était satisfaite, et b) le nombre d’étapes dans chaque courbe sera plus grand que le nombre d’événements dans chaque sous-groupe, donnant l’impression qu’il y a plus d’événements qu’il n’y en a vraiment.
CONCLUSIONS
La disponibilité de grands ensembles de données avec un suivi complet pour plusieurs paramètres ne cesse d’augmenter. Il existe également un besoin croissant d’analyses portant sur un critère d’évaluation précis, comme le décès par insuffisance cardiaque ou le contrôle des maladies ou le contrôle des maladies locales. Tous ces paramètres pourraient potentiellement avoir CR. Par conséquent, il est essentiel que le CR soit pris en compte dès la phase de conception jusqu’à l’interprétation des résultats. Bien que le modèle de PH de Cox puisse avoir une valeur limitée lorsque l’indépendance est prise en compte, les estimations du KM ne sont pas correctes et ne peuvent pas être interprétées. Ainsi, des techniques spécifiques telles que les modèles CIF et F & G disponibles en R et partiellement en STATA doivent être appliquées.
CONFLITS D’INTÉRÊTS
Aucun déclaré.