
Pour le concept d’identification du chiffre unitaire, nous devons d’abord nous familiariser avec le concept de cyclicité. La cyclicité d’un nombre quelconque concerne le dernier chiffre et la façon dont ils apparaissent d’une certaine manière définie. Prenons un exemple pour effacer cette chose:
Le diagramme de cyclicité de 2 est:
21 =2
22 =4
23 =8
24=16
25=32
Regardez de près ce qui précède. Vous verriez que comme 2 est multiplié à chaque fois avec son propre soi, le dernier chiffre change. À la 4ème multiplication, 25 a le même chiffre unitaire que 21. Cela nous montre que la cyclicité de 2 est 4, c’est-à-dire qu’après chaque quatrième multiplication, le chiffre unitaire sera deux.
Table de cyclicité:
La table de cyclicité pour les nombres est donnée comme ci-dessous:
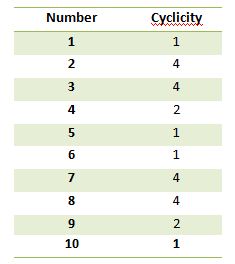
Comment avons-nous compris ce qui précède? Multipliez et voyez par vous-même. C’est une bonne pratique.
Utilisons maintenant le concept de cyclicité pour calculer le chiffre unitaire d’un nombre.
Quel est le chiffre unitaire de l’expression 4993 ?
Maintenant, nous avons deux méthodes pour résoudre ce problème, mais nous choisissons la meilleure façon de le résoudre, c’est-à-dire par cyclicité
Nous savons que la cyclicité de 4 est 2
Jetez un coup d’œil:
41 =4
42 =16
43 =64
44 =256
D’en haut, il est clair que la cyclicité de 4 est 2. Maintenant, avec le nombre de cyclicité, c’est-à-dire avec 2, divisez la puissance donnée, c’est-à-dire 993 par 2, quel sera le reste, le reste sera 1, donc la réponse lorsque 4 est élevé à la puissance est 4.Donc, le chiffre de l’unité dans ce cas est 4.
Pour vérifier si vous avez appris le sujet, pensez à un nombre comme celui-ci, calculez son chiffre unitaire, puis vérifiez-le à l’aide d’une calculatrice.
Remarque: Si le reste devient zéro dans tous les cas, le chiffre unitaire sera le dernier chiffre du nombre d’acyclicité
où a est le nombre donné et le nombre de cyclicité est représenté sur la figure ci-dessus.
Permet de résoudre un autre exemple:
Le chiffre à la place de l’unité du nombre 7295 X 3158 est
A. 7
B. 2
C. 6
D. 4
Solution
Le tableau de cyclicité pour 7 est le suivant:
71 =7
72 =49
73 = 343
74 = 2401
Divisons 295 par 4 et le reste est 3.
Ainsi, le dernier chiffre de 7295 est égal au dernier chiffre de 73 soit 3.
La table de cyclicité pour 3 est la suivante:
31 =3
32 =9
33 = 27
34 = 81
35 = 243
Divisons 158 par 4, le reste est 2. Par conséquent, le dernier chiffre sera 9.
Par conséquent, le chiffre de l’unité de (7925 X 3158) est le chiffre de l’unité du produit du chiffre à la place de l’unité de 7925 et 3158 = 3 * 9 = 27. Par conséquent, l’option 1 est la réponse.
