La valeur la plus utilisée dans un rapport sur le sol est probablement la capacité portante du sol. La raison évidente est que les exemples de base donnés dans la plupart des manuels utilisent presque toujours la capacité portante pour calculer la dimension du plan d’une semelle. En raison de sa simplicité et de sa facilité d’utilisation, cette méthode reste le paramètre fondamental du sol pour la conception des fondations. Cependant, cette simplicité suppose que le pied se comportera comme un corps rigide. Cette hypothèse particulière fonctionne bien dans la pratique pour les semelles à colonne petite et simple. Mais pour les fondations de grande taille et à colonnes multiples, la plupart des ingénieurs préfèrent une analyse flexible. Le calcul manuel d’une analyse flexible peut être difficile et, dans presque tous les cas, des logiciels tels que STAAD, SAFE, GT STRUDL, etc. sont utilisés. Cependant, ces programmes informatiques demandent souvent une entrée appelée « module de réaction de la plate-forme ». De nombreux ingénieurs ne connaissent pas ce terme et essaient souvent de le comparer à la capacité portante. Comme de plus en plus d’ingénieurs utiliseront des logiciels pour concevoir des fondations, il est essentiel pour les ingénieurs d’avoir une compréhension fondamentale de ce paramètre du sol. Existe-t-il une relation entre la capacité portante et le module de réaction de la plate-forme?
Module de réaction de la plate-forme (Ks)
Ce terme est mesuré et exprimé en intensité de charge par unité de déplacement. Pour le système d’unités anglais, il est souvent exprimé en kip / in2 / in; dans le système SI, il est exprimé en kN / m2 / m. Certains expriment ce terme en kip / in3 (ou kN / m3) ce qui peut être trompeur. Numériquement, kip /in3 est correct mais ne représente pas correctement la signification physique de la valeur mesurée et peut être confondu avec une unité de densité ou une mesure volumétrique.
Mathématiquement, le coefficient de réaction de la plate-forme est exprimé comme suit:
Ks = p / s (Eqn 1)
où p = intensité de pression de contact et s = tassement du sol
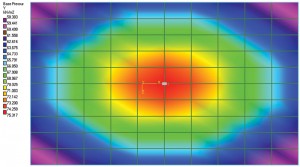
Figure 1a: diagramme de déviation et contour de pression du sol.
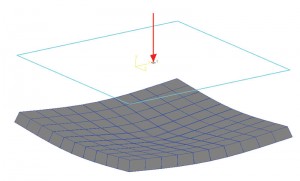
Figure 1b: Contour de pression du sol.
Comme l’a mentionné Terzaghi, une estimation correcte de la pression de contact pour une fondation flexible pourrait être très lourde, on suppose donc que Ks reste constant pour l’ensemble de la fondation. En d’autres termes, le rapport entre la pression et le tassement à tous les endroits d’un pied restera constant. Ainsi, le diagramme de déplacement d’une semelle avec une charge au centre aura un effet de bombage. Un point au centre de la semelle connaîtra le déplacement le plus élevé. Le déplacement diminue à mesure qu’il s’éloigne du centre. La figure 1a montre une fondation simple dalle sur sol. Il a été modélisé et analysé dans la fondation STAAD en tant que « Mat », qui est une fondation flexible; le sol a été défini en utilisant le coefficient de réaction de la plate-forme. Pour cet exercice, la valeur par défaut du logiciel pour le module de réaction de la plate-forme a été utilisée. Le diagramme de déplacement montre un effet de bombage comme discuté précédemment. La figure 1b montre le contour de la pression du sol. Il est également évident que l’intensité de pression au centre est maximale et diminue à mesure que les éléments (ou les coordonnées des nœuds) s’éloignent du centre. On pourrait donc supposer que le rapport entre l’intensité de la pression et le tassement est constant.
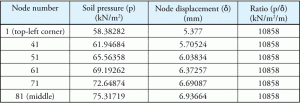
Tableau 1: Pression du sol, déplacement des nœuds et leur rapport.
Considérons certains des nombres du même exemple. La pression du sol, le déplacement correspondant et le rapport sont énumérés dans le tableau 1. Les points sont représentés sur une diagonale pour illustrer la variation de pression et de déplacement à mesure que les points s’éloignent du centre vers le point le plus éloigné dans le coin de la semelle rectangulaire. La figure 2 montre les points sur la dalle de tapis.
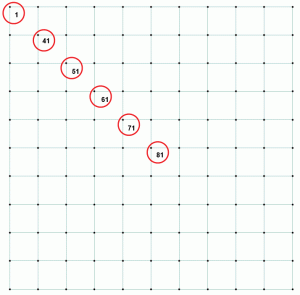
Figure 2: Points sélectionnés pour comparer la pression de base, la déflexion et le rapport.
Ce n’est guère une surprise car, par définition, le module de réaction de la plate-forme (Ks) est une constante pour l’ensemble de la semelle et le programme a utilisé Ks comme propriété du sol. Il est également important de noter que la valeur Ks par défaut du logiciel (10858 kN / m2 / m) était exactement la même que le rapport constant calculé dans le tableau 1.
La pression de base a été calculée à partir de la réaction de support. On pourrait penser que le rapport de réaction de support et de déplacement correspondant sera également une constante. Comme le montre le tableau 2, les rapports ne sont pas constants pour toutes les valeurs. Comment la valeur Ks est-elle utilisée dans le programme et comment la pression de base est-elle calculée?
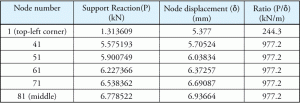
Tableau 2: Réaction et déplacement du support.
Zone tributaire
Souvent, une hypothèse est faite pour calculer la superficie d’une plaque pouvant être attribuée à un nœud ou, en d’autres termes, l’influence de chaque nœud sur la surface d’une plaque. Cela dépend de la forme de la plaque. Pour une plaque carrée ou rectangulaire parfaite, chaque nœud influencera exactement ¼ de la surface de la plaque (Figure 3a). Mais pour un quadrilatère généralisé, la meilleure pratique serait de calculer le centre de la masse de la plaque, puis de tracer des lignes de ce point central aux points centraux de chaque côté. Sur la figure 3b, la zone ombrée représente la surface d’influence du nœud correspondant.
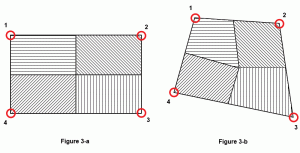
Figure 3: Zone tributaire du nœud.
Constante de support de ressort
Le calcul de la surface tributaire décrit ci-dessus est la procédure clé utilisée en interne par le logiciel commercial pour calculer la constante de ressort linéaire. Le programme calcule d’abord la zone tributaire pour chaque nœud de la semelle, puis multiplie le module de réaction de la plate-forme par la zone tributaire correspondante pour chaque nœud pour obtenir la constante de ressort linéaire à chaque nœud.
Kyi = Ks x Tai(Eqn 2)
où
Kyi est la constante de ressort au node nœud
Tai est la zone d’influence duth nœud
Ks est le module de réaction de la plate-forme
Pour une analyse de fondation en béton, ces ressorts doivent être défini comme uniquement par compression, car le béton est supposé ne supporter aucune force de traction. La pression de base est calculée au niveau de chaque nœud de support en divisant la réaction de support avec la zone tributaire du nœud correspondant. Si nous regardons l’exemple ci-dessus, le nœud 1 a une zone tributaire beaucoup plus petite que le reste des nœuds. On peut également noter que tous les autres nœuds ont la même zone tributaire. Ceci explique le tableau 2, car il montre que le rapport pour le nœud 1 est différent des autres nœuds. La figure 4 montre la zone tributaire pour différents nœuds. Le noeud 1 a une surface tributaire qui est de 25% du noeud 81. Le tableau 3 est une extension des tableaux 1 et 2 et montre comment le rapport constant est atteint pour tous les nœuds.
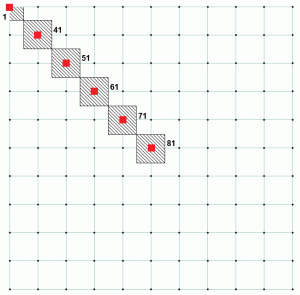
Figure 4: Zone tributaire des nœuds sélectionnés.
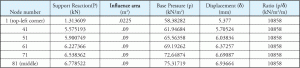
Tableau 3: Réaction, pression de base, déplacement, constante Ks.
Tassement admissible
La capacité portante est la mesure de la pression du sol qu’un sol peut supporter en toute sécurité. En d’autres termes, la capacité portante est la pression que le sol peut supporter avant qu’il ne tombe en panne. Les deux critères de défaillance du sol les plus importants sont:
- Rupture de cisaillement
- Tassement maximal admissible
Parmi de nombreux facteurs, la largeur de la fondation (B) peut influencer les critères de rupture. Normalement, la rupture de cisaillement régit les fondations plus petites et la rupture de tassement régit les fondations plus grandes. Le tableau 4 est un exemple typique qui montre la relation entre les différentes tailles de fondation et les critères de défaillance.
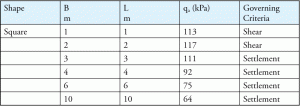
Tableau 4 : Capacité portante finale admissible pour un tassement admissible = 25 mm et une profondeur d’encastrement donnée.
Pour estimer l’échec du règlement, une valeur de règlement admissible est supposée (normalement 25 mm ou 1 pouce). Lorsque le sol se dépose plus que la valeur autorisée, le sol tombe en panne. Ainsi, même pour un calcul de la capacité portante, un tassement du sol admissible est utilisé et les ingénieurs en structure doivent être conscients de cette valeur lors de la conception d’une semelle. La valeur de tassement admissible du sol fait généralement partie intégrante de tout rapport sur le sol.
Pourquoi Utiliser le Module de réaction de la plate-forme
Il a été précédemment indiqué que pour concevoir une fondation de tapis flexible, le module de réaction de la plate-forme est utilisé à la place de la capacité portante du sol. Mais pourquoi? La réponse réside dans les hypothèses sous-jacentes du comportement d’une fondation.
Les fondations peuvent être rigides ou flexibles. La capacité portante est utilisée pour concevoir des fondations rigides, mais la réaction de la plate-forme est utilisée pour les fondations flexibles. L’hypothèse même d’une fondation rigide est que « la distribution de la réaction de la fondation p sur la base de la fondation doit être plane, car une fondation rigide reste plane lorsqu’elle se dépose. » Considérons un faisceau simplement supporté chargé en son centre, comme le montre la figure 5a. Par statique, on peut obtenir R1 = P/2 et R2 = P/2. Si le même faisceau est chargé de manière excentrique, la réaction peut être calculée comme indiqué à la figure 5b.
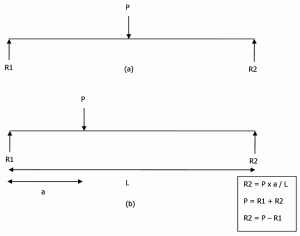
Figure 5: Réactions pour un faisceau simplement supporté.
Le même concept est étendu pour la conception de fondations rigides. Mais au lieu des supports finaux, toute la fondation est soutenue. On suppose également que la rigidité relative de la dalle de béton est beaucoup plus élevée que la rigidité du sol. Ainsi, la dalle est supposée rester plane même après l’application de la charge.
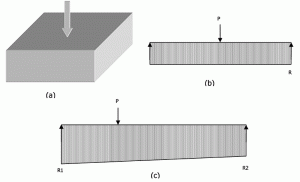
Figure 6: Réactions de sous-pente pour une semelle isolée.
La figure 6a montre une semelle chargée au centre. D’après une analogie de faisceau large rigide, P = R x L. De même, pour une semelle à charge excentrique, la réaction variera linéairement d’une extrémité à l’autre comme le montre la figure 6c. Les équations 3 et 4 peuvent être résolues pour trouver des réactions finales. Mais aucune des équations ne contient de module de réaction de base (Ks). Ainsi, la « distribution de la réaction de la plate-forme sur la base d’une semelle rigide est indépendante du degré de compressibilité de la plate-forme » sur laquelle elle repose. Comme de nombreux auteurs l’ont conclu, une fondation rigide peut être conçue en toute sécurité en utilisant la capacité portante, car dans la plupart des cas, cette méthode donne des résultats plus conservateurs.
P = 1 / 2L (R1 + R2) (Eqn 3)
P x a = 1 / 6B2R1 + 1 / 3B2R2 (Eqn 4)
Mais une fondation mat est souvent conçue comme une fondation flexible car elle peut être de grande taille et il peut y avoir de nombreux points d’application de charge et d’autres complexités, y compris des trous et des poutres de grade. La disponibilité généralisée des logiciels FEA contribue à cette tendance. Mais, contrairement aux fondations rigides, une fondation flexible ne peut pas avoir de réaction de fondation linéaire. Cela dépend plutôt de la compressibilité de la fondation ainsi que de la rigidité structurelle. Une fondation flexible est soumise à une flexion interne et à des déplacements relatifs entre deux points de dalle. Plus la rigidité structurelle est grande, moins le déplacement relatif est important. L’auteur a testé le boîtier avec une rigidité très élevée des éléments de la dalle, résultant en une surface presque plane après l’application de la charge. De même, plus le module de réaction de la plate-forme est élevé, moins la répartition de la pression est importante. En d’autres termes, une valeur Ks plus élevée absorbera plus de pression au point d’application de la charge. Par conséquent, le module de réaction de la plate-forme, qui est la fonction du tassement du sol et de la pression externe, est utilisé pour la conception flexible des fondations.
Corrélations
La réponse la plus courante – et probablement la plus sûre – à la question de la corrélation entre la capacité portante et le module de réaction de la plate-forme est qu’il n’y a pas de corrélation. Mais il devrait y en avoir un, car les deux sont les mesures des capacités du sol et l’un de ces deux paramètres peut être utilisé pour concevoir une fondation régulière.
Encore une fois, la définition de Ks est la pression par tassement unitaire. En d’autres termes, la capacité du sol à résister à la pression pour un déplacement donné. D’après les discussions antérieures, il est également clair que même la capacité portante a un règlement admissible. Il est donc tentant de conclure que le module de réaction de la plate-forme est la capacité portante par unité de tassement.
Cette conclusion est très similaire à l’équation présentée par Bowles.
SI: Ks = 40 (SF) qa kN/m3 (Eqn 5)
FPS: Ks = 12 (SF) qa k/ft3 (Eqn 6)
où SF = Facteur de sécurité et qa est la capacité portante admissible.
Dans les équations 5 et 6, la capacité portante admissible est d’abord convertie en capacité portante ultime en multipliant par un facteur de sécurité. L’auteur a supposé un tassement d’un pouce ou 25 mm. L’équation finale est ensuite formulée en divisant la capacité portante ultime par le tassement supposé.
La forme plus générique de l’équation peut s’écrire comme suit:
Ks = 
contrainte/déplacement (Eqn 7)
où
I = Facteur de sécurité
qa est la capacité portante admissible
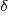est le tassement admissible du sol
Ces équations indiquent clairement que le facteur de sécurité approprié doit être utilisé et que la valeur Ks peut être mieux comparée à la capacité portante ultime plutôt qu’à la capacité portante admissible. Le facteur de sécurité peut varier en fonction des projets et des ingénieurs géotechniques. L’autre facteur important est le tassement admissible supposé pour la capacité portante calculée.
De même, il est à noter que les valeurs de pression de base rapportées par analyse FEA ne peuvent être directement comparées à la capacité portante. La pression de base maximale doit être multipliée par le facteur de sécurité, puis comparée à la capacité portante admissible du sol.
Cependant, les équations mentionnées ci-dessus ont des limites. Ils peuvent être appliqués à des semelles où règne une défaillance de tassement, mais ne peuvent pas être liés à des semelles où une défaillance de cisaillement se produit avant d’atteindre la limite de tassement admissible. Les ingénieurs doivent donc faire preuve de prudence avant d’utiliser ces équations.
Conclusion
La corrélation entre la capacité portante et le module de réaction de la plate-forme est au mieux une estimation. Il peut être utilisé pour l’estimation, mais une valeur Ks déterminée par un test de charge de la plaque devrait toujours être utilisée si elle est disponible ou devrait être demandée dans la mesure du possible. Cependant, la discussion ci-dessus donne un aperçu de ces valeurs et aide les ingénieurs à comprendre la signification physique du module de réaction de la plate-forme. Et, comme toujours, les ingénieurs en structure devraient consulter un ingénieur géotechnique avant de finaliser la rigidité du sol et les valeurs de roulement.▪