Transformation de chef de famille
La transformation de chef de famille (également « Réflexion de chef de famille ») est une transformation de réflexion orthogonale:
- il réflexe les vecteurs dans les colonnes de la matrice de telle sorte que
- le premier vecteur a tous les zéros sauf le premier élément
La matrice de transformation
Transformation par réflexion:
Propriétés
Les matrices de Householder sont symétriques et orthogonales: ce sont des matrices de réflexion
Dérivation
Nous avons doncPP = I-2vv^TT:
Nous utilisons de telles transformations pour la réinitialisation des éléments
Décomposition QR
Comme dans le cas de la Décomposition LU, où nous avons appliqué une série de Gauss Transformation des modifications, on peut faire de même et d’effectuer une série de Chef de ménage Transformations
- donc, si nous sélectionnons $y = \pm e_1$ (où $e_1$ est la matrice avec des 1 sur la position 1 et le repos sont des zéros)
- ensuite il permet de réinitialiser tous les éléments de $x$ à l’exception du premier
- donc, par le choix approprié de $H$, nous pouvons prendre en $A$ et zéro tous les sous-diagonale les éléments
- peuvent le faire plusieurs fois pour chaque colonne deAA$
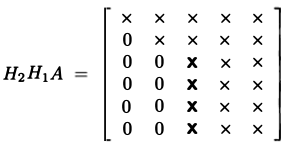
De cette façon, nous pouvons effectuer une décomposition QR:
Décomposition de Hessenberg
Au lieu de l’utiliser pour réduire la matrice en Triangulaire, nous pouvons utiliser la transformation de Householder pour réduire une matrice en matrice de Hessenberg