J’ai commencé à suivre le cours d’apprentissage automatique populaire d’Andrew Ng sur Coursera. La première semaine couvre beaucoup, du moins pour quelqu’un qui n’a pas touché beaucoup de calcul depuis quelques années
- Fonctions de coût (différence moyenne au carré)
- Descente de gradient
- Régression linéaire
Ces trois sujets étaient beaucoup à prendre en compte. Je vais parler de chacun en détail, et comment ils s’emboîtent tous, avec du code python à démontrer.
Modifier le 4 mai: J’ai publié un suivi axé sur le fonctionnement de la fonction de coût ici, y compris une intuition, comment la calculer à la main et deux implémentations Python différentes. Je peux faire une descente de gradient puis les rassembler pour une régression linéaire bientôt.
Représentation du modèle
Tout d’abord, l’objectif de la plupart des algorithmes d’apprentissage automatique est de construire un modèle: une hypothèse qui peut être utilisée pour estimer Y en fonction de X. L’hypothèse, ou modèle, mappe les entrées aux sorties. Ainsi, par exemple, disons que je forme un modèle basé sur un tas de données sur le logement qui incluent la taille de la maison et le prix de vente. En formant un modèle, je peux vous donner une estimation de combien vous pouvez vendre votre maison en fonction de sa taille. Ceci est un exemple de problème de régression — compte tenu de certaines entrées, nous voulons prédire une sortie continue.
L’hypothèse est généralement présentée comme

Les valeurs thêta sont les paramètres.
Quelques exemples rapides de la façon dont nous visualisons l’hypothèse:
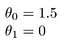
Cela donne h(x) = 1,5 + 0x. 0x signifie pas de pente, et y sera toujours la constante 1,5. Cela ressemble à:

Que diriez-vous
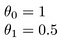

Le but de la création d’un modèle est de choisir des paramètres, ou des valeurs thêta, de sorte que h(x) soit proche de y pour les données d’apprentissage, x et y. Donc, pour ces données
x =
y =

Je vais essayer de trouver une ligne de meilleur ajustement en utilisant la régression linéaire. Commençons.
Fonction de coût
Nous avons besoin d’une fonction qui minimisera les paramètres de notre jeu de données. Une fonction courante souvent utilisée est l’erreur quadratique moyenne, qui mesure la différence entre l’estimateur (l’ensemble de données) et la valeur estimée (la prédiction). Cela ressemble à ceci:

Il s’avère que nous pouvons ajuster un peu l’équation pour rendre le calcul un peu plus simple. Nous nous retrouvons avec:
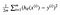
Appliquons cette fonction const aux données suivantes:

Pour l’instant, nous allons calculer certaines valeurs thêta et tracer la fonction de coût à la main. Puisque cette fonction passe par (0, 0), nous ne regardons qu’une seule valeur de thêta. À partir de là, je vais faire référence à la fonction de coût comme J (Θ).
Pour J(1), on obtient 0. Pas de surprise – une valeur de J(1) donne une ligne droite qui correspond parfaitement aux données. Que diriez-vous de J(0,5)?

La fonction MSE nous donne une valeur de 0,58. Tracons nos deux valeurs jusqu’à présent:
J(1) = 0
J (0,5) = 0.58

Je vais aller de l’avant et calculer d’autres valeurs de J (Θ).

Et si nous joignons bien les points ensemble…

Nous pouvons voir que la fonction de coût est au minimum lorsque thêta = 1. Cela a du sens — nos données initiales sont une ligne droite avec une pente de 1 (la ligne orange sur la figure ci-dessus).
Descente de gradient
Nous avons minimisé J (Θ) par essais et erreurs ci—dessus – juste essayer beaucoup de valeurs et inspecter visuellement le graphique résultant. Il doit y avoir un meilleur moyen? Descente de gradient de file d’attente. La descente de gradient est une fonction générale de minimisation d’une fonction, dans ce cas la fonction de coût d’erreur au Carré moyen.
La descente de gradient fait essentiellement ce que nous faisions à la main — changer les valeurs thêta ou les paramètres, petit à petit, jusqu’à ce que nous arrivions, espérons-le, au minimum.
Nous commençons par initialiser theta0 et theta1 à deux valeurs quelconques, disons 0 pour les deux, et partons de là. Formellement, l’algorithme est le suivant:

où α, alpha, est le taux d’apprentissage, ou à quelle vitesse nous voulons nous rapprocher du minimum. Si α est trop grand, cependant, nous pouvons dépasser.

Rassembler le tout — Régression linéaire
Résumant rapidement:
Nous avons une hypothèse:

que nous devons adapter à nos données d’entraînement. Nous pouvons utiliser une fonction de coût telle que l’Erreur Quadratique moyenne:

que nous pouvons minimiser en utilisant la descente de gradient:

Ce qui nous conduit à notre premier algorithme d’apprentissage automatique, la régression linéaire. La dernière pièce du puzzle que nous devons résoudre pour avoir un modèle de régression linéaire fonctionnel est la dérivée partielle de la fonction de coût:
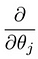
Qui s’avère être:
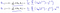
Ce qui nous donne une régression linéaire!
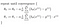
Avec la théorie à l’écart, je vais continuer à implémenter cette logique en python dans le prochain article.
Edit Le 4 mai: J’ai publié un suivi axé sur le fonctionnement de la fonction de coût ici, y compris une intuition, comment la calculer à la main et deux implémentations Python différentes. Je peux faire une descente de gradient puis les rassembler pour une régression linéaire bientôt.