a szerkesztő megjegyzése: Tony Abbey élő NAFEMS FEA osztályokat tanít az Egyesült Államokban, Európában és Ázsiában. Nafems e-learning órákat is tanít világszerte. Kapcsolat .a részletekért.
egy korábbi Desktop Engineering cikk (“egyszerűsítse a FEA szimulációs modelleket sík szimmetriával”) kifejtette, hogy még a nagy teljesítményű modern számítógépeknél is gyakran van motiváció az egyszerűsítési technikák alkalmazására a strukturális végeselem-elemzésben (FEA). Ez a nyomon követés leírja, hogy két szorosan kapcsolódó módszer hogyan használható 2D szeletek komplex struktúrán keresztül az érdekes régiókban. Az így kapott FEA modellek gyorsabban és hatékonyabban adhatnak értékes betekintést a helyi feszültségekbe, mint egy teljes 3D modell. Nem fogják elmondani az egész történetet, de értékes eszközök a CAE mérnök számára.
a két FEA módszert síkfeszültségnek és síkfeszültségnek nevezzük. Mindkettő 2D síkelemeket használ, amelyek vékony héjelemeknek tűnnek, és sík felületi geometriával vannak összekötve.
Síkfeszültség-Elemzés
Ábra. 1 mutatja a fontos tényeket sík stressz elemzés. Feltételezzük, hogy a szerkezeti régió a 2D xy síkban fekszik, a harmadik szerkezeti dimenzió viszonylag kicsi. Az ábrán ez a vastagság z irányban. A feszültségek a 2D síkban sigma x, sigma y (közvetlen feszültségek) és sigma xy (síkon belüli nyírófeszültség) néven léteznek. Ezen feszültségek mindegyike állandó a vastagságon keresztül, amint azt a betét mutatja. Ezenkívül nem lehet stressz a z irányban. Ezt a feszültség-alakváltozás anyagviszonyt az ilyen típusú elemzésben használt 2D síkfeszültség-elemek határozzák meg.
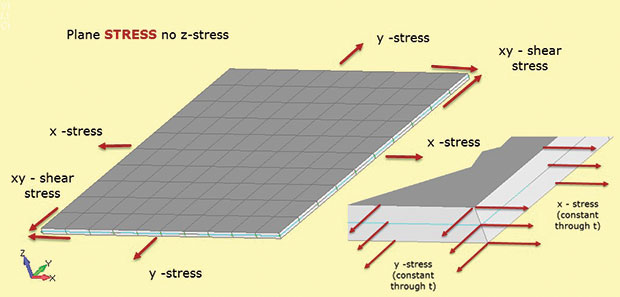ábra. 1: sík stressz; stresszállapot feltételezések.A z feszültség hiánya a módja annak, hogy emlékezzünk az elem típusjelölésére síkfeszültség (azaz csak a síkban lévő feszültségek megengedettek). Nincsenek átmenő vastagságú nyírófeszültségek is. Tudjuk betölteni a sík stressz modell ábra. 1 egy bi-axiális terhelés és kiszámítja sigma x és sigma y. Nincs sigma z. azt is kiszámítja a megfelelő síkban törzsek e-x és e-y.ha alkalmazzuk a nyírási terhelés, találunk nyírófeszültség sigma xy és nyírófeszültség e-xy. Érdekes módon kiszámíthatjuk az átmenő vastagság törzsét is e-z. ez nem nulla, mivel a modell szabadon elvékonyodhat z-ben, mivel X-ben és y-Ben húzódik. nincs síkon kívüli kényszer ennek megakadályozására. Néhány megoldóban visszanyerhetjük az E-z átmenő vastagságú törzset, és felhasználhatjuk a vastagság változásának kiszámításához. (Ha a modell kéttengelyes tömörítésben van, akkor a z szakasz vastagabb lesz). Ezt általában másodlagos törzsnek tekintik, és előfordulhat, hogy nem áll rendelkezésre a kimenethez—de ott van, és szükség esetén manuálisan kiszámítható.
ábra. 2 ábra egy alumínium fül alkatrész. A fül kiáll egy kompozit lemez layup, amely rétegek elhelyezni és ragasztott át a tangs (vagy lábak)és az alsó testrész. Az érintők a fülre gyakorolt terhelést továbbítják az összetett szerkezetbe. A gyakorlatban a rétegeket lépcsőznék, hogy lehetővé tegyék a kötésen keresztül a sima nyírást a kompozitba. A kompozitba történő nyírásátvitelt itt szórt felületi vonóerők szimulálják, amelyek” húzódnak ” a tangokra. Ezek kiegyensúlyozzák az alkalmazott fülterhelést.
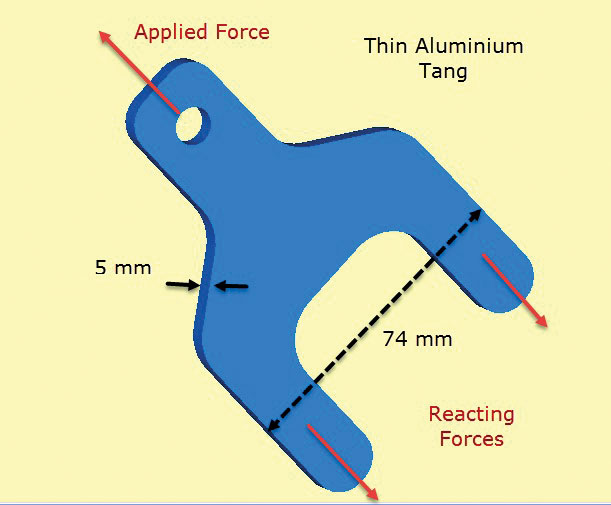ábra. 2: Vékony falú alumínium tang átadó terhelés kompozit szerkezet.a legfontosabb feltételezés itt az, hogy az átmenő vastagsági feszültségek nulla, a síkon belüli feszültségek pedig állandóak az alkatrész vastagságán keresztül. Ez azt jelenti, hogy a nyíróterhelés kompozitról Tangra történő átvitelének helyi részlete rosszul modellezett. Ennek az elemzésnek azonban az a célja, hogy ellenőrizze a fül és a tang keresztmetszetének méretét a kompozittól, síkon belüli feszültségek alkalmazásával.
az alkatrész vastagsága kicsi a többi mérethez képest. Ezt az értéket a sík feszültségelem meghatározásának tényleges vastagságaként adjuk meg.
ábra. A 3. ábra a FEA modellt és a számított maximális főfeszültségeket mutatja. Az érdeklődési területek a fül és a váll sugara körül vannak. A valós világban a stresszállapot a feszültségkoncentrációknál 3D lenne, és a vastagságon keresztül a sigma z feszültségek és a nyírófeszültségek helyileg egyensúlyoznának. Itt azonban nagyon ésszerű feltételezni, hogy a síkon belüli feszültségek dominálnak. Ez ugyanaz a feltételezés, amely implicit módon szerepel a kézikönyvekben található legtöbb hagyományos stresszkoncentrációs (kt) számításban.
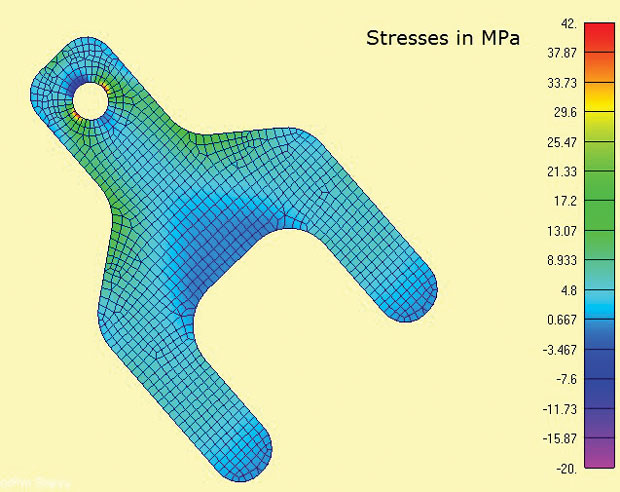3. ábra: 2D Síkfeszültség-elemek, amelyek maximális főfeszültséget mutatnaka síkfeszültség-elemzés egyik kényelmes tulajdonsága, hogy szigorúan 2D elemzés, tehát csak három szabadságfokot (DOF) kell korlátozni (síkban történő fordítások x, y és forgatás A z tengely körül). Ez alkalmas arra, hogy a 3-2-1 minimális kényszer módszer kiegyensúlyozott terhelés. 2D esetben ez 2-1 módszerre degenerálódik. Az egyik csomópont DOF x és y korlátozott, a másik megfelelő ortogonális csomópont DOF x korlátozott. Ez lehetővé teszi, hogy az érintőkben a reakcióterhelést közvetlenül szórt kiegyenlítő terhelésként alkalmazzák. Nehéz lenne szimulálni ezt a határfeltételt a földi korlátok révén.
másodlagos hatásként kiszámítható az E-z átmenő vastagságú törzs és így a Tang-ok elvékonyodása.
Sík Törzs Analízis
Ábra. A 4. ábra a sík törzs módszerének lényegét mutatja. Ismét 2D síkelemeket használnak, de finoman eltérő feltételezésekkel. Az x, y és xy síkon belüli feszültségek a korábbiakhoz hasonlóan alakulnak ki. Ezúttal azonban a síkon kívüli vagy a Z vastagságú törzs nullára van állítva. Tehát a síktörzs-elemzés csak a síkban lévő törzseket teszi lehetővé. Ez jól működik a bemutatott vastag szerkezetek ábrázolására. Ez azt is jelenti, hogy állandó vastagságú z feszültségek alakulnak ki a szerkezetben. Ezt a feszültség-alakváltozás anyagviszonyt az ilyen típusú elemzéshez használt 2D sík alakváltozási elemek határozzák meg.
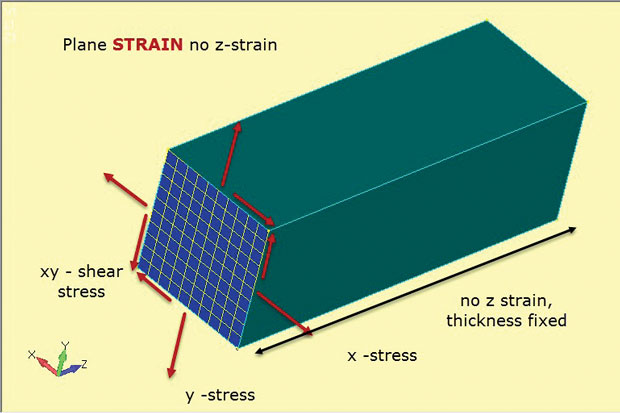ábra. 4: sík törzs analízis; stressz és törzs állapot feltételezések.az ábra a 2D síkfeszítő elemek tájolását mutatja vágott szakaszként egy tipikus mély komponensen keresztül. A feltételezés az, hogy ezen a vágási szakaszon a feszültségállapot megismétlődik bármelyiknél xy síkvágás (z állomás) az alkatrészen keresztül. Feltételezzük, hogy az alkatrész prizmatikus (állandó keresztmetszetű) hosszában.
a gyakorlatban ezt a módszert alkalmazzuk, ahol a feszültségállapot síkról síkra lassan változik egy mély komponensben. A mélységen keresztül elegendő anyagnak kell lennie ahhoz, hogy stabilizálja és megszüntesse az átmenő vastagságú törzset. Ugyanezt az elvet alkalmazzák az ábrán látható törésállósági mintákon is. 5. A vastag minta középső szakaszánál síkfeszítési körülmények között meghibásodás látható. A hiba a szabad élek és a vékony szakasz egy másik mód, több, mint egy sík feszültség állapotban. A sík törzs FEA modell definíció szerint jól reprezentálja a középvonal vastag mintájának viselkedését, de nem a szabad éleket vagy a vékony mintát.
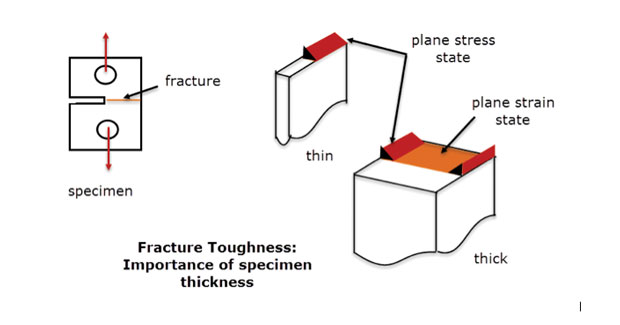ábra. 5: törésállóság példányok; vékony és vastag szakaszok.ábra. A 6. ábra egy kompozit szerkezetben használt másik komponenst mutat, amely ragasztott kötést képez. Itt a szakasz állandó és elég mély ahhoz, hogy feltételezhessük, hogy a feszültségek is állandóak a mélységgel. A szabad végfelület felületei (+z, -z) eltérő helyi stresszállapotúak lesznek (valójában síkfeszültség, amint azt megjegyeztük), azonban ennek az elemzésnek a célja a nettó szakasz feszültségének ellenőrzése a középvonalon (z = 0).
a 2D sík törzselemző háló a 3D komponensre van felosztva az ábrán. 7. A szakaszvágás A Z = 0 állomáson van meghatározva.
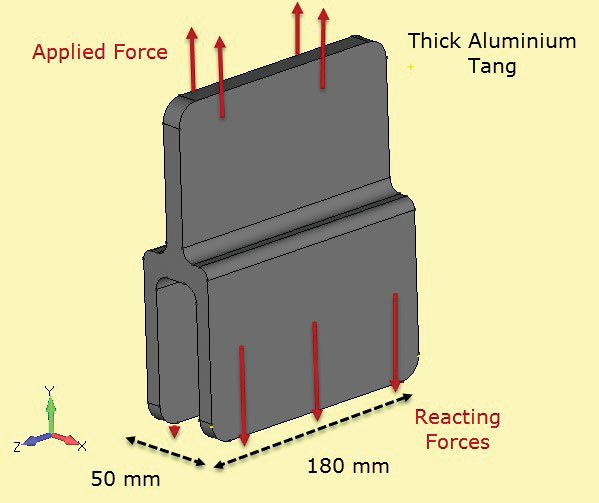6. ábra: mély keresztmetszetű alumínium tang.
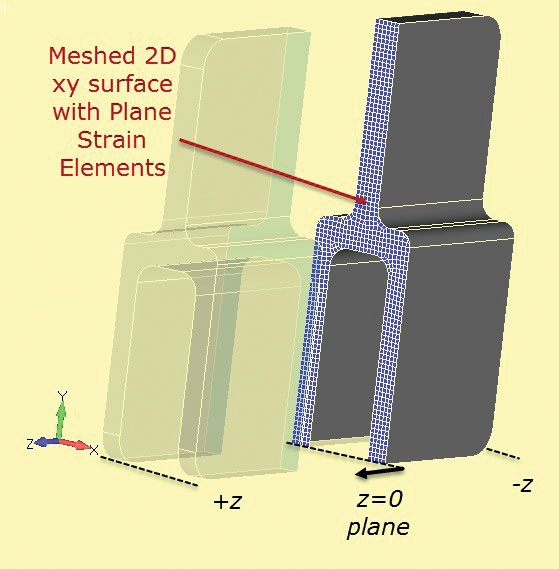ábra. 7: Szakasz vágja át a szilárd részt a 2D sík törzsszakasz kifejlesztéséhez.egy nagyon finom 2D sík törzs háló használható, amely nagyon gyorsan fut, mint egy teljes 3D modell. A 2-1 kényszer módszert a korábbiakhoz hasonlóan használják. A terhelést gondosan meg kell fontolni. A síkfeszítő szakasz “vastagsága” meglehetősen önkényes, alapértelmezés szerint általában 1,0-re van beállítva. Ha az alkatrész terhelését a mélységen keresztüli futó terhelésként számítják ki (N/m, Lbf/hüvelyk stb.) akkor ez az érték közvetlenül a sík törzshálón használható. Hasznos kiválasztani egy szakaszt, például az egyetlen tangot, és megbecsülni a névleges vagy átlagos feszültséget ebben a szakaszban a teljes komponensre. Ezt fel lehet használni, mint egy józanság ellenőrzés a sík törzs elemzés. A helytelen Betöltés valószínűleg a hiba fő oka ebben a módszerben.
az elemzés eredményeit az ábra mutatja. 8 és világosan mutassa meg a vállfilé körüli nagy feszültségű régiókat. A feszültségek a komponens központi mélységtartományára érvényesek (z = 0).
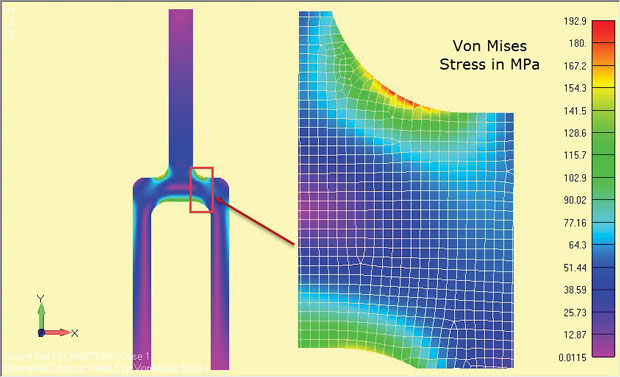ábra. 8: Egy mély tang komponens síktörzs-elemzési eredményei.az alkalmazott feszültségmennyiségek az alkalmazott megoldótól függenek. Néhány megoldó figyelmen kívül hagyja a Z irányú feszültségeket másodlagosnak, és helyreállítja a síkban lévő feszültségeket. A fő feszültségek és a von Mises feszültségek ezután egy 2D síkon belüli stresszállapotra vonatkoznak. Ha a z irányú feszültség helyreáll, akkor azt egyértelműen azonosítani kell, hogy az x-y síkban a 2D síkban lévő feszültségállapot azonosítható legyen.
pontosan mit jelent a z irányú feszültség? Ez a feszültség a zéró Z irányú törzs érvényesítése miatt alakult ki. A stressz úgy működik, mintha a prizmatikus szakasz szabad végfelületei rögzítve lennének. A mély szakasz komponensének központi síkján ezek lesznek a nulla Z irányú törzsállapot megtartásához szükséges kiegészítő feszültségek. A valóságban, ahogy a szabad felület felé haladunk, a z-feszültség nullára csökken, és sík feszültségeloszlássá válik (amint az a vastag törésmechanikai mintán látható).
sok esetben, mint például egy nyomás alatt álló henger, a végfelületeket lezárják, és valójában axiális feszültség alakul ki az axiális erők miatt. Ez más feszültség lesz, mint az indukált axiális feszültség a síktörzs-elemzésben. A tengelyirányú feszültségek kiszámításához kézi számításra lesz szükség, vagy lehetséges egy kiegészítő tengelyszimmetrikus modell nyomástartó edényekhez.
a geometria és a hálószerkezet könnyűsége jól alkalmazható a “mi lenne, ha” tanulmányokhoz vagy formálisabb alakoptimalizálási vizsgálatokhoz.
összehasonlításképpen a mély tang komponens fél szimmetriás teljes 3D elemzését végeztük, és az eredményeket az ábra mutatja. 9. A Névleges feszültség az egész felső egyetlen tang láb azonos mindkét esetben-ne feledje, ez az alapja minden józanság ellenőrzés.
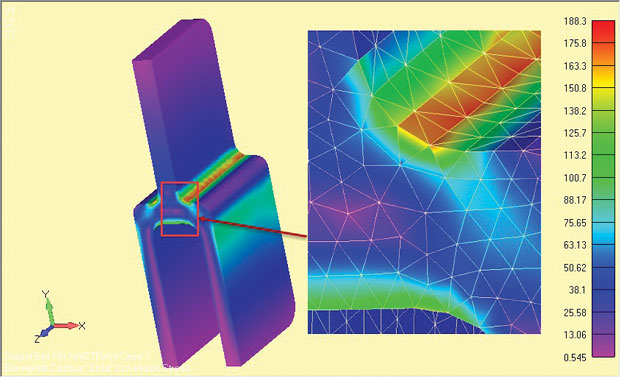ábra. 9: a mély tang teljes 3D modellje, stressz eredményeket mutatva.a helyi vállfeszültségek kis százalékkal alacsonyabbak a teljes modellben. Ennek három oka van. Először is, a viszonylag durva 3D tet háló rosszabb, mint a nagyon finom 2D sík törzs helyi háló. A 3D modell konvergenciaellenőrzését nem végezték el.
másodszor, a szabad felületek (+z, -z) geometriájában kis változás következik be a Z = 0 szakaszhoz képest a végfilé miatt. Ebben az esetben a hatás elhanyagolható, mivel a filé távol van a vállrégióktól. Sok összetevőben azonban helyi filé lesz, és elfogynak a részletek. amely megváltoztatja a geometriát egy egyszerű xy sík felületről. Előfordulhat, hogy a szabad végfelületeken a helyi stresszváltozásokat teljes 3D-s modellel kell megbecsülni vagy ellenőrizni.
végül, a sík törzs feltételezése rögzített z kényszer nál nél +z, – z szakaszok nem igaz véges mélységkomponensre. A z stressz nullára diffundál a “valódi” szabad arcoknál. Ezt a hatást az ábra mutatja. 10, amely a 3D-s modellt használja, ahogy van, valamint a Z-feszültség síktörzsének szimulációjaként.
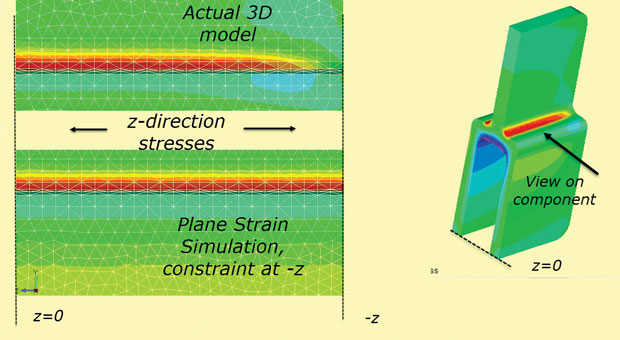ábra. 10: A z-stressz diffúziója a szabad felület felé.gyors és hatékony
a Síkfeszültség és a sík törzs elemzése hasznos 2D módszerek, amelyek gyakran kiegészíthetik a teljes körű 3D modelleket. Nem minden tulajdonság ábrázolható, de némi találékonysággal legalább meg lehet becsülni a kulcsfontosságú területek stresszét. A módszerek használatának motivációja a gyors, hatékony elemzés lehetővé tétele egyszerű 2D geometriával és hálószerkezettel.