bevezetés
a Versengő kockázatokat (Cr) a 18.század óta a time-to-event elemzés speciális eseteként ismerik el. Időnként a statisztikai vagy matematikai területen végzett munka új fejlesztéseket tartalmaz, beleértve David és Moeschberger monográfiáját.1 ahogy az adatok kiterjedtebbé, világosabbá és pontosabbá váltak a különböző típusú kimenetelek tekintetében, a CR az eseménytől az eseményig tartó elemzés kulcsfontosságú típusaként jelent meg, amely a betegség jobb megértéséhez szükséges. A matematikai eredmények és az alkalmazott mező közötti kapcsolatot meg kellett teremteni. Számos szerző hozzájárult a CR helyzetek megértéséhez.2, 3 más szerzők továbbfejlesztették és fejlesztették a technikákat, és egyes esetekben használatra kész számítógépes kódot bocsátottak rendelkezésre az alkalmazott statisztikákhoz.4, 5, 6
bevezetés a TIME-to-EVENT elemzésbe
sok tanulmányban az eredményt hosszirányban figyelik meg. Ily módon a kohorsz minden alanyát megfigyelik egy ideig, amíg az esemény meg nem történik. Például érdekes esemény lehet halál, szívroham vagy rák kiújulása. A vizsgálat célja lehet az esemény előfordulásának valószínűségének becslése vagy annak összefüggése az érdekes kovariánsokkal, például a kezeléssel vagy az alany jellemzőivel. Az alkalmazott statisztikai elemzést time-to-event elemzésnek vagy néha túlélési elemzésnek nevezzük. Az esemény valószínűségének becslésére a leggyakoribb módszer egy nem paraméteres megközelítés, amelyet általában Kaplan-Meier-nek hívnak7 (KM) vagy termékhatár módszer. A túlélés KM-becslésének fő feltételezése az, hogy a cenzúrázott megfigyelések elég hosszú ideig követik az eseményt.
a cikk többi részében az esemény valószínűségét adják meg, nem pedig az esemény nélküli valószínűséget. Például a túlélés valószínűsége helyett a halál valószínűségét mutatják be, amelyet a KM-becslő kiegészítésével lehet megbecsülni: 1-KM.
bevezetés a Versengő KOCKÁZATOKBA
nem ritka, hogy egy tanulmány résztvevője egynél több típusú eseményt tapasztal. CR helyzet akkor fordul elő, amikor az egyik típusú esemény előfordulása megváltoztatja az érdekes esemény megfigyelésének képességét. Miyasaka et al.8 végzett egy tanulmányt egy közösségi alapú kohorsz diagnosztizált betegek pitvarfibrilláció között 1986 és 2000 Olmsted County, Minnesota, Egyesült Államok. Az elsődleges eredmény a demencia kialakulása volt. A medián követési idő 4,6 év volt. Más típusú események voltak a stroke és a halál. A pitvarfibrillációban szenvedő 2837 személy közül 299-nek volt demenciája, 1638 pedig az elemzés idejére meghalt. A stroke-ot nem jelentik, és az elemzés során cenzúrázzák. A tanulmány következtetése az volt, hogy a demencia előfordulása a pitvarfibrillációban szenvedő egyének körében gyakori (10,5% 5 év alatt KM módszerrel). A demencia előtti stroke előfordulása nem befolyásolja a demencia megfigyelését, ezért nem CR esemény. Az érvelés kedvéért figyelmen kívül hagyjuk azt a tényt, hogy a többszörös stroke demenciát okozhat. Másrészt az előzetes demencia nélküli halál lehetetlenné teszi a demencia megfigyelését. Ezért a demencia nélküli halál CR esemény a demencia végpontjára. Szintén súlyos fejsérülés CR eseménynek tekinthető, mivel a beteg viselkedésbeli változásai lehetetlenné tehetik a demencia diagnózisát.
finomabb CR helyzet fordul elő a Whalley et al.9 az echokardiográfia fontosságáról. Ez a 228 idős tüneti betegből álló kohorsz echokardiográfián esett át, amelyet kardiovaszkuláris kórházi kezelés vagy kardiovaszkuláris halálozás követett. A hipotézis az volt, hogy az echokardiográfia jellemzői előre jelzik a kardiovaszkuláris eseményeket. A fő végkövetkeztetést a cardiovascularis halálozást és/vagy hospitalizációt magában foglaló összetett mérésként határozták meg. Az ilyen típusú kimenetel esetén a szív-és érrendszeri betegségektől eltérő okok miatt bekövetkező halál CR esemény, és mint ilyen, a beteget már nem fenyegeti az érdekes események bármelyike.
egy 3 karos, kettős-vak, randomizált vizsgálatot végeztek 931 központon és 24 országon keresztül, hogy teszteljék a valzartán vs valzartán+kaptopril vs kaptopril önmagában (VALIANT)10 hatását az összmortalitásra. Összesen 14 703 myocardialis infarctus utáni, bal kamra diszfunkcióban és/vagy szívelégtelenségben szenvedő beteg 1:1:1 arányban emelkedett a 3 karon. Mivel minden halált eseménynek tekintettek, az ilyen típusú eredménynek nincs CR. A tanulmány alátámasztotta azt a hipotézist, miszerint a 3 kar túlélése eltérő volt. A gyomor-bélrendszeri (GI) vérzést azonban mind a 3 karban súlyos mellékhatásként azonosították. Moukarbel et al.11 tanulmányozta azokat a lehetséges tényezőket, amelyek megjósolhatják a GI vérzést. Erre a végpontra a GI vérzés nélküli halál egyértelmű CR.
egyre több kutató ismeri fel a CR jelenlétét és a megfelelő technikák alkalmazásának szükségességét. Egy 972, nem ST-szegmens emelkedésű akut koronária szindrómában szenvedő betegből álló kohortot vizsgáltak 2001 és 2005 között N ons et al.12 a vizsgálat egyik célja az akut szívelégtelenség rehospitalizációjával kapcsolatos tényezők megtalálása volt. A vizsgált tényezők között szerepelt a cukorbetegség, az ischaemiás szívbetegség korábbi története, a krónikus veseelégtelenség, a dohányzás története és a kezelés története. A szerzők felismerték a CR lehetőségét, mint például a rehospitalizáció előtti halál, és helyesen alkalmaztak speciális technikákat a CR helyzetének figyelembevételére.
Melberg et al.13 1234 tüneti koszorúér-betegségben szenvedő betegből álló kohortot vizsgált, akik 2 típusú kezelést kaptak: koszorúér bypass oltás (n=594) vagy perkután koszorúér-beavatkozás (n=640). A nyomon követés során megfigyelt 301 haláleset 42,5% – a volt szívhalál, a többi pedig nem szívhalál. A szerzők az összes okból bekövetkező mortalitásra, valamint a szívhalandóságra és a nem szívhalandóságra vonatkozó eredményeket mutatják be. Rámutatnak arra, hogy az összes okból bekövetkező halálozás százalékos aránya a cardialis és nem cardialis mortalitás százalékos arányának összege, amelyet helyesen becsülnek meg, figyelembe véve a CR-t. A szerzők hangsúlyozzák az egyes érdekes események elemzésének fontosságát, ahelyett, hogy azokat általános halálozássá egyesítenék. Ez a téma is kifejtette általánosabb szinten Mell és Jeong.14
amint az a fenti példákból feltételezhető, a fő kérdés, amikor CR jelen van, az, hogy figyelmen kívül hagyja-e a CR-t, és cenzúrázza-e a CR-t érintő megfigyeléseket, vagy elszámolja-e a CR-t. Amikor a CR-t figyelmen kívül hagyják, és a CR-megfigyeléseket cenzúrázzák, az elemzés egy “szokásos” eseményig tartó forgatókönyvre redukálódik. Az ilyen típusú elemzések ismerete és a szoftverek rendelkezésre állása miatt sok kutató ezt a megközelítést alkalmazza, amint az a korábbi példákban is látható. Azonban egyhangúlag egyetértenek nemcsak a statisztikusok között2, 15, 16, 17, 18, hogy az esemény valószínűségének becslése ebben az esetben túlbecsüli a valódi valószínűséget. A következő természetes kérdés az, hogy a modellezés végrehajtható-e ezeken a határokon belül (figyelmen kívül hagyva/cenzúrázva a CR-t). Ez kétértelműbb és nehezebb megérteni. Bár egy ilyen elemzés nem lehet értéktelen, értelmezése szinte mindig nehézségekkel jár. A fő követelmény az, hogy a CR esemény (amelynek megfigyeléseit cenzúrázták és összekeverik a valódi cenzúrázott megfigyelésekkel) függetlennek kell lennie az érdekes eseménytől. Ha ez a helyzet, akkor az eredményeket úgy lehet értelmezni, mint a kovariánsok hatását, amikor a CR események nem léteztek. Ezt a feltételezést azonban általában nem lehet megtenni, nem lehet ellenőrizni vagy tesztelni. Összefoglalva, minden alkalommal, amikor a CR megfigyeléseket cenzúrázzák, az esemény valószínűségének becslése helytelen, és a kovariánsok hatásának értelmezése nem egyértelmű, mivel nem ismerik az érdekes esemény és a CR esemény közötti függetlenséget.
ha az elemzést CR-re számolva végezzük (és az érdekes eseménytől vagy a cenzúrázástól elkülönítetten kódoljuk), akkor a valószínűséget helyesen becsüljük meg, és a modellezés egyértelmű értelmezéssel rendelkezik. Nincs feltételezés a függetlenségről, amely akadályozná az értelmezést. Az így becsült kovariáns együtthatója képviseli ennek a kovariánsnak a megfigyelt valószínűségekre gyakorolt hatását.
több szerző19, 20 szimulációk segítségével próbálta összehasonlítani a két megközelítést a tesztek ereje szempontjából. A kutatónak azonban tisztában kell lennie azzal, hogy a fő probléma az eredmények értelmezésében rejlik. Függetlenül attól, hogy mennyire erősek a tesztek, az elemzésnek meg kell válaszolnia a tanulmány kérdését.
az esemény valószínűségének becslése
általános gyakorlat a KM módszer alkalmazása egy esemény valószínűségének becslésére. A KM-becslés tipikus képlete
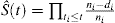
, ahol a t1t2t3ni a ti időpontban veszélyeztetett betegek számát, A di pedig a ti időpontban bekövetkezett események számát jelenti.
ez a képlet algebrai manipulációval átalakítható az esemény valószínűségének kifejezésére:
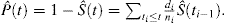
CR jelenlétében legalább 2 típusú esemény létezik: érdekes esemény, amelyet az e alindex azonosít, és a Versengő kockázati esemény, amelyet a c alindex azonosít. Kalbfleisch és Prentice bevezette a CR jelenlétében érdekes esemény valószínűségének képletét:
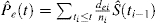
érdekes az (1) és (2) közötti kapcsolat. Mivel di az összes esemény száma a ti-nél, felfogható az érdeklődésre számot tartó események számának összegeként dei és a CR események száma DCI a ti időpontban. Mint ilyen, bármilyen típusú esemény valószínűsége a következőképpen bontható le:
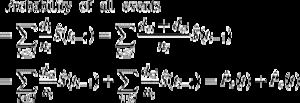
így az összes esemény valószínűsége lebontható az egyes eseménytípusok valószínűségeiben.
ha 1 KM-t használunk egy érdekes esemény valószínűségének kiszámításához CR jelenlétében, a (2) képletben szereplő összes esemény túlélése helyébe a csak az érdekes eseményeken alapuló KM-becslés lép. Ez torzítja az eredményeket, amint azt később bemutatjuk. A KM módszer alkalmazásának fő feltételezése az, hogy a cenzúrázott betegek, ha elég hosszú ideig követik őket, végül megtapasztalják az eseményt. Ha azonban a KM-módszert CR jelenlétében alkalmazzák, akkor az érdeklődésre számot tartó eseményektől eltérő típusú eseményeket tapasztaló betegeket általában cenzúrázzák, annak ellenére, hogy már nem veszélyeztetik őket az érdeklődésre számot tartó esemény. Ezenkívül a (3)-ban látható szép bomlás nem hajtható végre az 1 KM-es képletnél.
alkalmazott helyzetekben lehetséges, hogy számos más típusú esemény is létezik, amelyek nem érdekesek. Ebben az esetben minden csoportosítható a CR események égisze alatt.
egy példán keresztül mutatjuk be, hogy a KM módszer használata nem megfelelő CR jelenlétében.
a példa leírása
a Hodgkin-limfóma kezelésének késői hatásainak tanulmányozására összegyűjtött adatkészletet használjuk illusztráció. A fő eredmény a szívbetegség kórházi kezelése. A Hodgkin limfóma egy olyan típusú rák, amely úgy tűnik, főleg a fiatal felnőttek. Korai szakaszában szinte gyógyítható, 10 éves teljes túlélése 70%. Így ezeknek a betegeknek a kohorszja ideális a kezelés hosszú távú mellékhatásainak tanulmányozására. Az itt használt adatkészlet egy nagyobb kohorsz részhalmaza,amelyet másutt jelentenek. Az adatokat is módosítjuk, hogy a mi céljainkat szolgálják. Például az egyszerűség kedvéért csak azokat a betegeket tartottuk az adatokban, akik kemoterápiában vagy sugárterápiában részesültek, kivéve a kombinált kezelést. A CR arányának növelése érdekében (halál szív kórházi kezelés nélkül) minden stádiumú beteget bevontunk. Néhány nyomon követési és halálozási dátumot beszámítottak. Az adatok módosításai miatt ebből az elemzésből nem lehet klinikai következtetéseket levonni. Az itt bemutatott adatok 689 nyilvántartást tartalmaznak, 93 szívkórházzal és 467 halálesettel.
a kardiális kórházi ápolás és a kardiális esemény nélküli halál arányát mind a KM módszer (1), mind a kalbfleisch és a Prentice21 által erre a célra bevezetett kumulatív incidencia funkció (CIF) alkalmazásával számítjuk ki (2).
a Versengő kockázati helyzetekre alkalmazott Kaplan-Meier-módszer túlbecsüli az esemény valódi arányát
az 1.ábra csak a kemoterápiával kezelt csoport szív hospitalizációjára vonatkozó CIF-és 1 KM-es becsléseket mutatja be. Az 1 KM-es becsléseknek megfelelő törött vonal a CIF-becsléseket képviselő folytonos vonal felett van. Matematikailag kimutatható, hogy az 1 KM mindig túlbecsüli az esemény valószínűségét. Általános tévhit, hogy az 1 KM-es becslések helyesek, ha a két esemény független. Az események közötti függetlenség legjobb esetben is mindig megkérdőjelezhető, de még akkor is, ha az adatokat független eseményként szimulálják, a CIF-becslések és az 1 KM közötti különbség létezik. A különbség nagysága az események számától függ, mind az érdekes események, mind a CR események esetében. In Miyasaka et al., 8 a demencia előfordulása 5 év alatt a KM módszerrel 10,5% volt. A CR (halálozások) száma az események teljes számának körülbelül háromnegyede volt, ami arra utal, hogy becslésük sokkal nagyobb lehet, mint amit megfigyeltek.
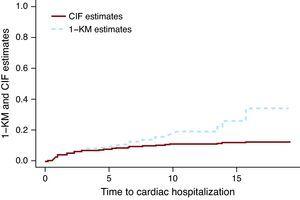
1. ábra. Kumulatív incidencia függvény vs 1-Kaplan-Meier becslések.. CIF, kumulatív incidencia függvény; KM, Kaplan-Meier.
a kumulatív incidencia függvény bármely esemény valószínűségét (szív kórházi ápolás vagy halál) elválasztja az alkotó Valószínűségekbe
Algebrailag ezt a (3). A működésének mélyebb megértése érdekében azonban grafikusan megmutatjuk, hogy az összes esemény valószínűségétől kezdve egy rész részt vesz az egyik esemény CIF-jében, a másik pedig a másik esemény CIF-jében. A 2A. ábra bármely esemény valószínűségét mutatja: szív kórházi kezelés vagy halál szív kórházi kezelés nélkül. A 2B. ábra csak a 10,7 és 10 közötti görbét tartalmazza.85 év, úgy, hogy a lépések láthatóak legyenek. Minden lépésnél van egy kör. A nyitott körök azokon a lépéseken jelennek meg, amelyekben halált figyeltek meg, míg a szilárd körök azokon a lépéseken vannak, amelyekben szív kórházi ápolás történt. A szilárd körökkel rendelkező lépések részt vesznek a CIF-ben a C panelben a szív kórházi ápolásában, a nyitott körökkel rendelkezők pedig a 2D. ábra halál görbéjében vesznek részt.így minden lépés hozzájárul az azt okozó esemény valószínűségéhez. Ily módon bármely időpontban az összes esemény valószínűsége az érdekes esemény valószínűségének és a CR valószínűségének összege. Vegye figyelembe, hogy az utolsó 3 panel (2b-D ábra) ugyanazt az időablakot mutatja, és ugyanolyan hosszú az y tengelyre, hogy a lépések mérete összehasonlítható legyen közöttük. Az 1. táblázat ezeket a valószínűségeket mutatja az 1., 2., 3., 4. és 5. évben.
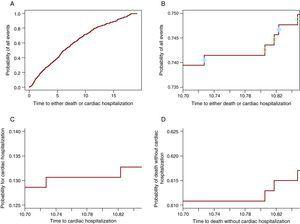
2. ábra. Az összes esemény valószínűségének felosztása az alkotó valószínűségekbe. A. a szív kórházi kezelésének vagy halálának valószínűsége. B. a szív kórházi kezelésének vagy halálának valószínűsége csak az időablakban 10,70-10,85 év. A szilárd körök a szív kórházi ápolását, a nyitott körök pedig a szív kórházi ápolása nélküli haláleseteket jelzik. C. a szív kórházi kezelésének valószínűsége az időablakban 10,70 -10,85 év. D. a halál valószínűsége szív kórházi kezelés nélkül az időablakban 10.70-10.85.
1.táblázat. Bármely esemény valószínűsége az alkotó valószínűségek összege.
| jelentéstétel éve | a szív hospitalizációjának valószínűsége | a halál valószínűsége | a szív hospitalizációjának vagy a halál valószínűsége |
| 1 | 0.038 | 0.054 | 0.092 |
| 2 | 0.054 | 0.139 | 0.193 |
| 3 | 0.072 | 0.193 | 0.265 |
| 4 | 0.076 | 0.25 | 0.327 |
| 5 | 0.087 | 0.305 | 0.392 |
mivel az 1 KM túlbecsüli egy esemény valószínűségét, ha megpróbálnánk hozzáadni a szív kórházi kezelésének 1 KM-es becsléseit a halál 1 KM-jéhez, akkor sokkal nagyobb arányt érnénk el, mint bármely esemény valószínűsége. Bizonyos esetekben a kapott szám még nagyobb, mint 1, ami azt bizonyítja, hogy CR jelenlétében az 1 KM-es becslések nem is valószínűségek.
a kumulatív incidencia függvény módszer valóban becsüli-e az esemény helyes valószínűségét?
erre a célra egy 500 rekordból álló adatkészletet szimuláltak úgy, hogy 5 év előtt ne legyen cenzúra, és 2 típusú esemény létezik: 1.típusés 2. A 2. táblázat az egyes eseménytípusok esetében mutatja az addig az időpontig megfigyelt számot, a nyers arányt és a CIF-becslést, amelyek pontosan megegyeznek. Az egyenlőség csak akkor következik be, ha addig az időpontig nincsenek cenzúrázott megfigyelések. A bejelentett években cenzúrázott megfigyelések jelenlétében az egyenlőség nem áll fenn, és a valószínűség becslésének helyes módja a CIF, nem pedig a nyers Arány.
2.táblázat. A kétféle esemény valószínűsége, ha legfeljebb 5 évig nincsenek Cenzúrázott megfigyelések.
CIF, kumulatív incidencia funkció.
összefoglalva, a CR jelenlétében bekövetkező esemény valószínűségének kiszámításához a Kalbfleisch és Prentice által bevezetett módszert kell használni, amelyet általában kumulatív előfordulási görbének neveznek.
modellezés
az elemzés fontos szempontja a kovariáns és az érdekes esemény közötti összefüggés tesztelése, akár önmagában, akár más tényezőkhöz igazítva. CR hiányában ezt rutinszerűen a Cox arányos veszélyek (Cox PH) modell.22
CR jelenlétében a Cox PH-modellnek nincs egyszerű értelmezése. Ha a 2 típusú eseményhez való idő függetlennek tekinthető, akkor az eredmények úgy értelmezhetők, hogy a CR nem létező helyzetben mutatják a hatást. A függetlenség feltételezését azonban ritkán lehet elvégezni vagy tesztelni, így a Cox PH-modell eredményei általában nem értelmezhetők.
Fine és Gray modell
Fine és Gray6 (F&G) módosították a Cox PH modellt, hogy lehetővé tegyék a CR jelenlétét. A technikai módosítás abból áll, hogy a CR-megfigyeléseket csökkenő súly mellett tartják a kockázatkészletben. Ily módon az F&G módszer modellezi a részeloszlási veszélyeket. Az F&G modell alapján becsült hatás a terápiás csoportok közötti jelenlegi és valós különbségeket mutatja a részeloszlási veszélyek arányában. A veszélyek arányosságának feltételezése továbbra is követelmény, de természetesen az elosztási veszélyekre utal. Az F&G modell időfüggő együtthatókat képes befogadni a veszélyek nem időszerűségének modellezésére. Ez a modell alkalmazható mind az érdekes eseményre (szív kórházi ápolás), mind a CR-re (halál).
a Cox PH és F& G modelleket alkalmazták a Hodgkin lymphoma adatkészletre a kemoterápia és a sugárzás kezelési lehetőségének tesztelésére. Ebben a példában (3. táblázat) a Cox PH és az F&G modellek eredményei jelentősen eltérnek (első 2 sor). Mint már említettük, a Cox PH-értékek nem értelmezhetők és nem használhatók. A második sor azt mutatja, hogy több Szívkórház van a sugárzási csoport között, a harmadik sor pedig több halálesetet mutat a kemoterápiás csoport között. A 3. ábra ezeket az eredményeket grafikusan mutatja be. Lehetséges, hogy a kemoterápiát csak előrehaladott betegségben szenvedő betegeknek adták, és ezek a betegek nagyobb valószínűséggel haltak meg rákban. Másrészt önmagában a sugárzást valószínűleg korai stádiumban adták azoknak a betegeknek, akik hosszabb ideig éltek a Hodgkin-limfóma diagnózisa után. Ezeknek a betegeknek nagyobb esélyük volt késői mellékhatások, például szívbetegség kialakulására.
3.táblázat. A kezelés hatása Cox arányos veszélyek és finom és szürke modellek esetén.
CI, konfidencia intervallum; Cox PH, Cox arányos veszélyek modellje; F& G, finom és szürke modell; HR, relatív hazárd.
a relatív hazárdok a sugárterhelési csoport veszélyeinek növekedését mutatják a kemoterápiás csoporthoz képest.
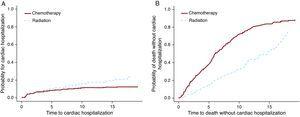
3. ábra. A kezelés hatása a szív kórházi ápolására és a halálra.
mint ebből a példából látható, az eredmények értelmezése a statisztikus és a klinikus közötti együttműködés munkája, aki alapos ismeretekkel rendelkezik a betegségről.
a CR jelenléte bonyolítja mind az adatok elemzését, mind értelmezését. Annak érdekében, hogy az olvasó helyesen értelmezze az eredményeket, a szerzőknek részleteket kell tartalmazniuk A megfigyelt eseményekről, annak ellenére, hogy első látásra nem tűnnek fontosnak. Ezért, amikor a végpontot idővel megfigyelik, a szerzőknek fel kell tüntetniük az érdekes eseményt, hogy fennáll-e a CR lehetősége, hány beteg tapasztalja az ilyen típusú események bármelyikét, valamint a nyomon követés időtartama. CR jelenlétében informatív az érdekes esemény elemzése, valamint a CR elemzése, mivel ezek kiegészítik egymást, és segíthetnek az eredmények értelmezésében.
a logisztikai megközelítés
tegyük fel először, hogy a no CR keretein belül vagyunk. 1 év), sok kutató számára a választott eszköz a logisztikai regresszió. Ez akkor megfelelő, ha a kohorsz minden egyénének van a minimális nyomon követése, ebben az esetben 1 év. Valójában az 1 éves halálozás becslése egybeesik az 1 KM-es becsléssel. Az időbeli határpontnak azonosnak kell lennie a kohorsz minden egyes személyénél. Ezért, ha az érdeklődés eredménye 1 éves halálozás és 1 egyén a kohorszban 1 év és 2 nap múlva meghal, ezt a személyt “1 éves eseménynek” kell tekinteni.”Ez csökkentheti az események számát, ami az ideálisnál kevesebb elemzést eredményez, amikor sok megfigyelt esemény bekövetkezik a küszöbérték után.
ugyanazok az alapvető szabályok érvényesek, ha CR van jelen. A kohorsz minden egyénének rendelkeznie kell a minimális nyomon követési ponttal, amelyet időhatárként kell kiválasztani, és ennek a határértéknek a kohorsz minden tagjára vonatkoznia kell. Az együtthatók és a p-értékek általában ugyanazt az üzenetet adják, de a logisztikai regresszió esetében nem lesznek pontosan azonosak az F&G modellhez képest. Először is, a logisztikai regresszióban az együttható az esélyhányados naplóját képviseli, míg az F&G modellben a veszélyek részeloszlásainak arányának naplója. Ezenkívül a logisztikai elemzésben nem minden eseményt használnak, és természetesen egy másik modellt használnak.
TELJESÍTMÉNYSZÁMÍTÁS
ha az intézkedés eseményig tart, akkor a teljesítményszámításnak két szakasza van. Az első lépés az események számának kiszámítása, amelyek egy adott hatásméret észleléséhez szükségesek. Ezután kiszámítják az események számának megfigyeléséhez szükséges betegek számát. Az előző szakaszokban hangsúlyozták, hogy amikor CR jelen van, a CR előfordulása miatt nem lehet megfigyelni az összes érdekes eseményt. Mivel az események száma központi szerepet játszik a teljesítmény kiszámításában, különös figyelmet kell fordítani a CR figyelembevételére. Ha a CR-t nem veszik figyelembe, akkor a tanulmány alulteljesített lesz, ezért valószínűleg sikertelen (és esetleg etikátlan).
szoftver
a nyílt forráskódú R szoftver a CRAN (the Comprehensive R Archive Network) oldalon (http://cran.r-project.org/) egy csomagot (cmprsk) kínál, amelyet Dr. Robert Gray tartalmazza a szükséges eszközöket a teljes elemzés számviteli CR. Így megkaphatjuk a megfigyelt valószínűségi diagramokat az érdekes eseményre és egy p-értéket Gray-teszt alapján, amely egy módosított logrank teszt a CR helyzetre. A csomagon belül van egy funkció az F&G megközelítéssel történő modellezéshez is. Luca Scruca fokozta a modellezési funkció kimeneti kézbesítését a könnyebb olvasás érdekében azáltal, hogy a csomagba egy összefoglaló típusú függvényt épített be. A modell lehetővé teszi a veszélyek arányosságának ellenőrzését, valamint az időfüggő együtthatók feltételeit. A kód nem tudja befogadni a bal csonkolási vagy fürtadatokat. A bal csonkolás hasznos lenne betegenként több / visszatérő esemény elemzéséhez vagy az eset kohorsz elemzéséhez. Kidolgozták az eset-kohorsz vizsgálatok kódját (Pintilie et al.23) és a szerzőktől beszerezhető. Zhou et al.24 kiterjesztette az F&G modellt a rétegzett adatok befogadására, és lesz egy verziója a fürtadatok számára is. Ezen a ponton a kód mindkét esetben beszerezhető a szerzőktől, de valószínű, hogy benyújtják a CRAN-hoz.
a STATA 11 nemrégiben vezette be az F& G modellt. Tisztában kell lenni azzal, hogy a STATA segítségével kapott gráfok inkább prediktív, mint megfigyelt valószínűségi gráfok. Két figyelmeztetés van az előre jelzett görbék használatakor: a) a vonalak mindig úgy jelennek meg, mintha a veszélyek arányossága teljesülne, és b) az egyes görbék lépéseinek száma nagyobb lesz, mint az egyes alcsoportok eseményeinek száma, azt a benyomást keltve, hogy több esemény van, mint valójában.
következtetések
a nagy adatkészletek elérhetősége több végpont teljes nyomon követésével folyamatosan növekszik. Egyre nagyobb szükség van olyan elemzésekre is, amelyek olyan pontos végponttal foglalkoznak, mint a szívelégtelenség okozta halál vagy a betegség ellenőrzése vagy a helyi betegség ellenőrzése. Mindezek a végpontok potenciálisan CR-vel rendelkezhetnek. Ezért elengedhetetlen, hogy a CR-t a tervezési szakasztól az eredmények értelmezéséig figyelembe vegyék. Míg a Cox PH-modell értéke korlátozott lehet, ha a függetlenséget vesszük figyelembe, a KM-becslések nem helyesek és nem értelmezhetők. Ezért olyan speciális technikákat kell alkalmazni, mint a CIF és az F&G modellek, amelyeket R-ben és részben STATA-ban bocsátottak rendelkezésre.
összeférhetetlenség
nincs bejelentve.