Hővezető képesség

a szilárd anyagok hővezető képessége eltérő természetű, attól függően, hogy vezetők-e vagy sem. A szabad elektromos töltések nélküli dielektrikumokban a hőenergiát fononok továbbítják. A kristályrácsban lévő atomok kollektív rezgései elmozdulási hullámok formájában jelentkeznek, amelyek interferenciája hullámcsomagokat, azaz fononokat generál. Az elmozdulási hullámok a sűrűség ingadozásait idézik elő, amelyek a törésmutató variációjaként nyilvánulhatnak meg. Ha a hullámok áthaladnak egy olyan régión, amelyben a törésmutató eltér az átlagos térfogatértéktől, akkor a hőmozgás energiáját hordozó későbbi elmozdulási hullámok szétszóródnak.

a szórás annál erősebb, annál nagyobb az atomok maximális eltérése a rácsban lévő átlagos helyzetüktől, azaz minél nagyobb a T. Ez magyarázza azt a kísérletileg megállapított tényt, hogy a kristálydielektrikumok hővezetőképessége meglehetősen magas hőmérsékleten csökken: ^ 1/T (1.ábra).

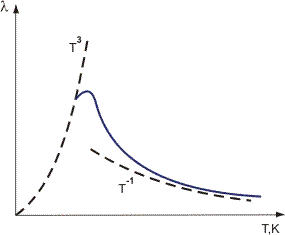
1.ábra. A kristálydielektrikumok hővezető képességének változása a hőmérséklettel.

Debye a kvantummechanikai koncepciók keretein belül betekintést engedett az alacsony T-nél bekövetkező, csúcsszerű(t) variációba. Kidolgozta a dielektrikumok dipóluselméletét, amely a molekula mint merev dipólus fogalmán alapul. Ebben a modellben Debye bevezette az úgynevezett Debye-hőmérséklet fogalmát, amely arányos az atom rezgések maximális frekvenciájával egy szilárd anyagban. A legtöbb anyag esetében a gmbh vagy alacsonyabb, vagy közel van a szobahőmérséklethez (kivételt képez a gyémánt, amelynél a CA = 1850 K, és a berrylium, amelynél a CA = 1160 K).

a szilárd anyagok kvantumelméletében a kristályrácsot fonongázzal töltött térfogatnak tekintik, amelyre a legegyszerűbb kinetikai elmélet levonását alkalmazzák

ahol c egy dielektrikum hőkapacitása, amely egybeesik a fonongázéval, v A fononok átlagos sebessége megközelítőleg megegyezik a hangsebességgel,a fononok átlagos szabad útja. A bizonyos véges érték megléte a fonon szóródásának eredménye a fononokon, a kristályrács hibáin és különösen a teljes minta szemcsehatárain. A hőmérséklet-függőséget a(T)és a (C) hőmérséklet határozza meg.

magas hőmérsékleten, amely lényegesen meghaladja a Debye hőmérsékletet, a – et korlátozó alapmechanizmus egy fonon-fonon szórás, amely a kristály atom rezgéseinek anharmonikussága miatt következik be. A hőellenállás phonon-phonon mechanizmusa ((1/6) a hőellenállás együtthatója) csak a phonon-áramlás késleltetését és a kvázi-lendület észrevehető változását eredményező átmenet miatt valósítható meg. Minél nagyobb a T, annál nagyobb az átmenet valószínűsége csökkenéssel:(1/T). Mivel T-nél > 6d a c hőkapacitás csak kis mértékben növekszik a hőmérséklettel, ezért a C 1 / T.

a Debye-hőmérsékletnél alacsonyabb hőmérsékleteken, T<<xhamd, a phonon-phonon szórás által meghatározottátlagos szabad út hossza drasztikusan növekszik,expu xhamd/T, és szabályként az R kristály méretére korlátozódik.a Debye-törvény szerint a C hőkapacitás ebben a hőmérsékleti tartományban változik, mivel c (T/ons)3. Következésképpen T 0-nál a hővezetési együtthatónak a T3 arányában csökkennie kell. Azt a hőmérsékletet, amelynek a hővezető képessége csúcsértékkel rendelkezik, CA-tól határozzuk meg, amely általában megfelel T 0,05 CA-nak.

ez az elmélet a hővezetési együttható viselkedését is figyelembe veszi olyan amorf anyagok esetében, amelyeknek nincs hosszú távú sorrendje, Vagyis “kristályaik” mérete atomméretek sorrendje. Ennek értelmében ezeknek az anyagoknak a “határainál” szóródásnak kell érvényesülnie Minden T és const esetén. Az amorf anyagok hővezetési együtthatója 6 T3 alacsony hőmérsékleten, és mérsékelt és magas hőmérsékleten a hőkapacitással arányosan enyhén növekednie kell, T > 6d.

mindez kvalitatív magyarázatot ad a valós kristálydielektrikumokban fennálló függőségre, de nem veszi figyelembe az állandó rácstól való eltéréseket más elemek és saját izotópjaik atomszennyeződése miatt. Magas hőmérsékleten a szennyeződések által a hőszállítással szembeni ellenállás független a hőmérséklettől. Ez lehetővé teszi a kristálytisztaság mértékének becslését a hővezető képesség hőmérsékletének változásából. Ugyanez a tény lehetővé teszi számunkra, hogy meghatározzuk az üveges és kristályos anyag eloszlását a természetes ásványban, ha az üveget a kristály szennyeződésének tekintjük.

a fémek hővezető képessége az áramhordozók, azaz a vezető elektronok mozgásától és kölcsönhatásától függ. Általában a relatív hővezető képesség λ egy fém egyenlő az összeg rács (phonon) λph, elektron λe alkatrészek, λ = λe + λph; az átlagos hőmérséklet, mint általában, λe >>λph.

ha a gázok egyszerű kinetikus elméletét alkalmazzuk a szabad elektronok áramlására, és feltételezzük, hogy szabad útjuk hossza nem függ a sebességtől, akkor az elmélet azt sugallja, hogy

ahol e az elektrontöltés, K Boltzrnann-állandó, és az elektromos vezetőképesség, ha az elektrontöltés, ha az elektrontöltés. A szigorú kvantummechanikai elmélet hasonló összefüggést kínál,

mindkét képletben úgy tűnik, hogy a hővezetési együttható elektron részének aránya a hővezetési együtthatóhoz képest a villamos vezetőképességhez képest széles hőmérsékleti tartományban arányos a Wiedemann-Franz törvény szerinti hőmérséklettel, az L, ahol L A Lorentz-szám. Ezt a törvényt használják az amplitúdó kiszámításához a mért elektromos vezetőképességből. Azonban az alábbi hőmérsékleteken sérül 6d amikor egy elektron-fonon kölcsönhatás érvényesül (a kontinensek csökkenő T−vel nőnek, mint T−5, míg le kissé változik, mint T-2).

a kísérleti eredmények azt bizonyítják, hogy a fémek hővezető képessége magas hőmérsékleten általában a hőmérséklet kissé csökkenő függvénye. De sok kivétel van. Így a vas hővezető képessége erősen csökken a hőmérséklettel, míg a tantál és a nióbium pozitív hőmérsékleti együtthatót mutat.

érdekesek azok a kísérletek, amelyek összehasonlítják a különböző anyagok hővezetési együtthatóit egyetlen jellemző hőmérsékletre, például a szilárd anyagok TM olvadáspontjára. Így a Missenard által végzett kísérleti adatok statisztikai feldolgozása azt mutatta, hogy a fémek hővezető képessége az olvadáspontnál(CA) (t = Tm) = 6385>, míg a dielektromos kristályok hővezető képessége t = Tm esetén, ahol m a molekulatömeg, N az atomok száma a kémiai képletben, a denzitás, és a TM olvadáspontja Kelvinben van.

a félvezetőkben a hőtranszport összetettebb, mint a dielektrikumokban és a fémekben, mivel a fonon és az elektron komponensek egyaránt nélkülözhetetlenek számukra. A komplexitás másik oka a szennyeződések jelentős hatása, bipoláris diffúzióés más kevéssé tanulmányozott tényezők a hőátadásra.

a nyomásnak a szilárd anyagok hővezető képességére gyakorolt hatása jó pontossággal feltételezhető, hogy lineáris, sok P-vel növekvő fém esetében.

a porozitásnak a szilárd anyagok hővezető képességére gyakorolt hatásáról lásd: porózus közeg.