valószínűleg a legszélesebb körben használt érték a talaj jelentés a talaj teherbíró képességét. A nyilvánvaló ok az, hogy a legtöbb tankönyvben szereplő alapvető példák szinte mindig teherbírást használnak a talp tervméretének kiszámításához. Az egyszerűség és a könnyű használat miatt ez a módszer továbbra is az alapozás tervezésének alapvető talajparamétere. Ez az egyszerűség azonban feltételezi, hogy a talp merev testként fog viselkedni. Ez a feltételezés jól működik a gyakorlatban a kis és egyoszlopos lábazatoknál. De a nagy és több oszlopos alapok esetében a legtöbb mérnök a rugalmas elemzést részesíti előnyben. A rugalmas elemzés kézi kiszámítása kihívást jelenthet, és szinte minden esetben olyan szoftverprogramok, mint a STAAD, a SAFE, a GT STRUDL stb. használják. Ezek a számítógépes programok azonban gyakran “subgrade reakció modulusának”nevezett bemenetet kérnek. Sok mérnök nem ismeri ezt a kifejezést, és gyakran megpróbálja összehasonlítani a teherbírással. Mivel egyre több mérnök használ szoftvert az alapok tervezéséhez, elengedhetetlen, hogy a mérnökök alapvető ismeretekkel rendelkezzenek erről a talajparaméterről. Van-e összefüggés a teherbírás és a szubgrád reakció modulusa között?
a Szubgrád reakció modulusa (Ks)
ezt a kifejezést az elmozdulás egységére eső terhelésintenzitásban mérik és fejezik ki. Az angol egységrendszer esetében gyakran kip/in2/in; az SI rendszerben kN/m2/m. egyesek ezt a kifejezést kip/In-ben fejezik ki3 (vagy kN/m3), ami félrevezető lehet. Számszerűen a kip / in3 helyes, de nem megfelelően képviseli a mért érték fizikai jelentőségét, és összetéveszthető sűrűségegységgel vagy térfogatméréssel.
matematikailag a szubgrád reakció együtthatóját a következőképpen fejezzük ki:
Ks = p/s (Eqn 1)
ahol p = érintkezési nyomás intenzitása és s = talajtelepülés
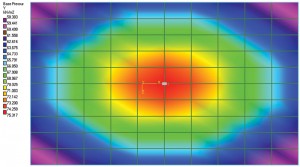
1a. ábra: alakváltozási diagram és talajnyomás-kontúr.
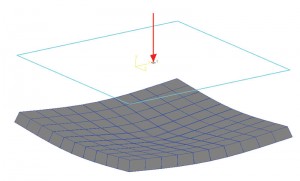
1b.ábra: talajnyomás kontúrja.
mint Terzaghi említette, a rugalmas alapozás érintkezési nyomásának megfelelő becslése nagyon nehézkes lehet, ezért feltételezzük, hogy a Ks állandó marad az egész talpon. Más szavakkal, a nyomás és a kiülepedés aránya a talp minden helyén állandó marad. Tehát a középpontban lévő terhelésű lábazat elmozdulási diagramja dishing hatással lesz. A talp közepén lévő pont a legnagyobb elmozdulást fogja tapasztalni. Az elmozdulás csökken, amikor elmozdul a központtól. Az 1a ábra egy egyszerű födém-on-grade alapot mutat. A Staad Foundation-ben “Mat” – ként modellezték és elemezték, ami egy rugalmas alap; a talajt a szubgrád reakció koefficiensével határoztuk meg. Ehhez a gyakorlathoz a szoftver alapértelmezett értékét használtuk az algrád reakció modulusához. Az elmozdulási diagram a korábban tárgyalt dishing hatást mutatja. Az 1b. ábra a talajnyomás kontúrját mutatja. Az is nyilvánvaló, hogy a középpontban a nyomás intenzitása maximális, és csökken, Amikor az elemek (vagy csomópontkoordináták) elmozdulnak a középponttól. Tehát feltételezhető, hogy a nyomásintenzitás és a település aránya állandó.
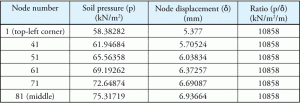
1. táblázat: talajnyomás, csomópont-elmozdulás és arányuk.
tekintsünk néhány számot ugyanabból a példából. A talajnyomást, a megfelelő elmozdulást és az arányt az 1. táblázat tartalmazza. A pontok átlósan vannak ábrázolva, hogy bemutassák a nyomás és az elmozdulás változását, amikor a pontok elmozdulnak a középponttól a téglalap alakú lábazat sarkában lévő legtávolabbi pontig. Ábra 2 mutatja a pontokat a szőnyeg födém.
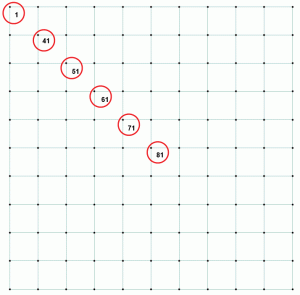
2. Ábra: Kiválasztott pontok az alapnyomás, az elhajlás és az arány összehasonlításához.
ez aligha meglepő, mivel definíció szerint a szubgrád reakció modulusa (Ks) állandó az egész talajra, és a program a KS-t használta talajjellemzőként. Fontos megjegyezni azt is, hogy a szoftver alapértelmezett Ks értéke (10858 kN/m2/m) pontosan megegyezett az 1.táblázatban kiszámított állandó hányadossal.
az Alapnyomást a támasztó reakcióból számítottuk ki. Azt gondolhatnánk, hogy a támogató reakció és a megfelelő elmozdulás aránya is állandó lesz. Amint a 2. táblázat mutatja, az arányok nem állandóak minden értéknél. Hogyan használják a programon belül a Ks értéket és hogyan számítják ki az alapnyomást?
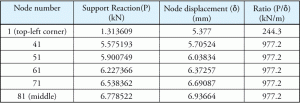
2. táblázat: támogató reakció és elmozdulás.
mellékfolyó terület
gyakran feltételezik, hogy kiszámítják, hogy egy lemez mekkora területe tulajdonítható egy csomópontnak, vagy más szavakkal, az egyes csomópontok hatása a lemez felületére. A lemez alakjától függ. Tökéletes négyzet vagy téglalap alakú lemez esetén az egyes csomópontok pontosan befolyásolják a lemez felületének xhamsterét (3a ábra). De egy általánosított négyszög esetében a legjobb gyakorlat az lenne, ha kiszámolnánk a lemez tömegének középpontját, majd vonalakat rajzolnánk az adott középponttól az egyes oldalak középpontjáig. A 3b ábrán az árnyékolt terület a megfelelő csomópont befolyási felületét képviseli.
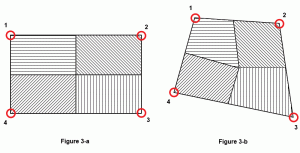
3. ábra: csomópont mellékfolyó területe.
Rugótartó állandó
a fent leírt mellékfolyóterület-számítás a legfontosabb eljárás, amelyet a kereskedelmi szoftver belsőleg használ a lineáris rugóállandó kiszámításához. A program először kiszámítja a mellékfolyó területét a lábazat minden csomópontjához, majd megszorozza az algrád reakció modulusát az egyes csomópontok megfelelő mellékfolyó területével, hogy megkapja az egyes csomópontoknál a lineáris rugóállandót.
Kyi = Ks x Tai (Eqn 2)
ahol
Kyi a rugóállandó az i-edik csomópontnál
Tai az i-edik csomópont befolyási területe
Ks a szubgrád reakció modulusa
a beton alapozásának elemzéséhez ezeket a rugókat a csak tömörítésként definiálva, mivel feltételezzük, hogy a beton nem hordoz húzóerőt. Az alapnyomást minden támasztó csomópontnál úgy számítjuk ki, hogy a támasztó reakciót elosztjuk a megfelelő csomópont mellékfolyó területével. Ha megnézzük a fenti példát, az 1. csomópontnak sokkal kisebb mellékfolyó területe van, mint a többi csomópontnak. Azt is meg lehet jegyezni, hogy az összes többi csomópontnak ugyanaz a mellékfolyója. Ez magyarázza a 2. táblázatot, mivel azt mutatja, hogy az 1.csomópont aránya eltér a többi csomóponttól. A 4.ábra a különböző csomópontok mellékfolyóterületét mutatja. Az 1. csomópontnak van egy mellékfolyó területe, amely a 81.csomópont 25% – a. A 3. táblázat az 1.és 2. táblázat kiterjesztése, és bemutatja, hogyan érhető el az állandó arány az összes csomópont esetében.
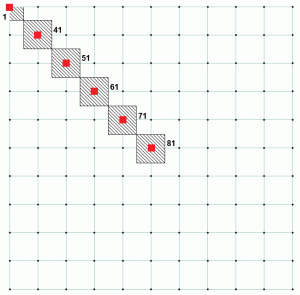
4. ábra: a kiválasztott csomópontok mellékfolyója.
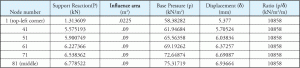
3. táblázat: reakció, alapnyomás, elmozdulás, Ks állandó.
megengedett település
teherbírás a talajnyomás mérése, amelyet a talaj biztonságosan elviselhet. Más szavakkal, a teherbírás az a nyomás, amelyet a talaj képes ellenállni, mielőtt meghibásodik. A két legfontosabb talajhibás kritérium a következő:
- nyírási hiba
- maximálisan megengedett település
számos tényező közül az alapzat szélessége (B) befolyásolhatja a meghibásodási kritériumokat. Általában a nyírási hiba a kisebb alapokra, az elszámolási hiba pedig a nagyobb alapokra vonatkozik. A 4. táblázat egy tipikus példa, amely bemutatja a különböző alapméretek és a meghibásodási kritériumok közötti kapcsolatot.
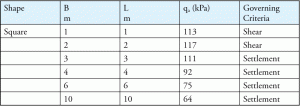
4. táblázat: megengedett végső teherbírás a megengedett kiegyenlítéshez = 25 mm és egy adott beágyazási mélység.
a kiegyenlítési hiba becsléséhez megengedett kiegyenlítési értéket kell feltételezni (általában 25 mm vagy 1 hüvelyk). Ha a talaj a megengedett értéknél többet települ, a talaj meghibásodik. Tehát még a teherbírás kiszámításához is megengedett talajtelepítést használnak, és a szerkezeti mérnököknek tisztában kell lenniük ezzel az értékkel, amikor egy alapot terveznek. A megengedett talajtelepítési érték általában szerves része bármely talajjelentésnek.
miért használjuk a Szubgrád reakció modulusát
korábban kijelentettük, hogy a rugalmas szőnyegalap kialakításához az algrád reakció modulusát használjuk a talaj teherbírása helyett. De miért? A válasz abban rejlik, hogy az alapítvány hogyan viselkedhet.
az alapok lehetnek merevek vagy rugalmasak. A teherbírást merev alapok tervezésére használják, de a subgrade reakciót rugalmas alapokra használják. A merev alapozás nagyon feltételezése az, hogy ” a subgrade reakció eloszlása O az alapzat alapja felett síknak kell lennie, mert egy merev alap sík marad, amikor leülepszik.”Vegyünk egy egyszerűen támogatott gerendát, amely a közepén van betöltve, amint az az 5a ábrán látható. a statika segítségével R1 = P/2 és R2 = P/2. Ha ugyanaz a sugár excentrikusan van betöltve, a reakció az 5b. ábrán látható módon számítható ki.
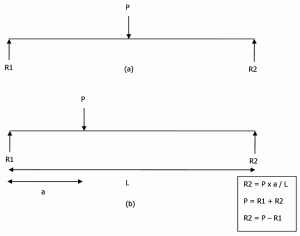
5. ábra: Reakciók egy egyszerűen támogatott sugárhoz.
ugyanezt a koncepciót kiterjesztik a merev alapozás kialakítására is. De a végtámogatások helyett az egész alapot támogatják. Azt is feltételezzük, hogy a betonlap relatív merevsége sokkal magasabb, mint a talaj merevsége. Tehát feltételezzük, hogy a lemez a terhelés alkalmazása után is sík marad.
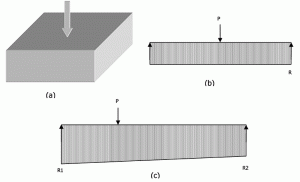
6. ábra: másodlagos reakciók izolált lábazatra.
a 6a.ábra egy középen betöltött lábazatot mutat. Merev széles sugár analógiából, P = R x L. Hasonlóképpen, excentrikusan terhelt lábazat esetén a reakció lineárisan változik egyik végétől a másikig, amint azt a 6C. ábra mutatja.a 3. és 4. egyenletek megoldhatók a végreakciók megtalálásához. De egyik egyenlet sem tartalmazza az algrád reakció modulusát (Ks). Tehát a “subgrade reakció eloszlása a merev lábazat alapján független az subgrade összenyomhatóságának mértékétől”, amelyen nyugszik. Mint sok szerző arra a következtetésre jutott, a merev alapot biztonságosan meg lehet tervezni teherbírással, mivel a legtöbb esetben ez a módszer konzervatívabb eredményeket hoz.
P = 1/2L(R1 + R2) (Eqn 3)
P x a = 1/6b2r1 + 1/3b2r2 (Eqn 4)
de a szőnyegalapot gyakran rugalmas alapként tervezik, mivel nagy méretű lehet, és sok terhelési pont és egyéb bonyolultság lehet, beleértve a lyukakat és a gerendákat. A FEA szoftverek széles körű elérhetősége hozzájárul ehhez a tendenciához. De a merev alapokkal ellentétben a rugalmas alapozásnak nem lehet lineáris subgrade reakciója. Inkább az alap összenyomhatóságától, valamint a szerkezeti merevségtől függ. A rugalmas alapot belső hajlításnak és relatív elmozdulásoknak vetik alá két födémpont között. Minél nagyobb a szerkezeti merevség, annál kisebb a relatív elmozdulás. A szerző a födémelemek nagyon nagy merevségével tesztelte az esetet, ami a terhelés alkalmazása után majdnem sík felületet eredményezett. Hasonlóképpen, minél nagyobb a szubgrád reakció modulusa, annál kisebb a nyomáseloszlás. Más szavakkal, a magasabb Ks érték nagyobb nyomást fog elnyelni a terhelés alkalmazási pontján. Ezért a modulus a subgrade reakció, amely a funkciója a talaj település és a külső nyomás,használják rugalmas Alapítvány tervezés.
korrelációk
a teherbírás és a szubgrád reakció modulusa közötti korreláció kérdésére a leggyakoribb – és valószínűleg a legbiztonságosabb – válasz az, hogy nincs korreláció. De kell lennie egynek, mivel mindkettő a talaj kapacitásának mérése, és e két paraméter bármelyike felhasználható egy szabályos alap kialakításához.
ismét a KS meghatározása az egységnyi településenkénti nyomás. Más szavakkal, a talaj kapacitása, hogy ellenálljon egy adott elmozdulás nyomásának. A korábbi megbeszélésekből az is egyértelmű, hogy még a teherbírás is megengedett. Ezért csábító azt a következtetést levonni, hogy a szubgrád reakció modulusa az egységnyi településenkénti teherbírás.
ez a következtetés nagyon hasonlít a Bowles által bemutatott egyenlethez.
SI: Ks = 40(SF)qa kN/m3 (Eqn 5)
FPS: Ks = 12(SF)qa k/ft3 (Eqn 6)
ahol SF = biztonsági tényező és qa a megengedett teherbírás.
az 5.és 6. egyenletben a megengedhető teherbírást először a biztonsági tényezővel való szorzással a végső teherbírásra kell átszámítani. A szerző egy hüvelyk vagy 25 mm-es települést feltételezett. A végső egyenletet ezután megfogalmazzuk, elosztva a végső teherbírást a feltételezett rendezéssel.
az egyenlet általánosabb formája a következőképpen írható:
Ks = 
feszültség/elmozdulás (Eqn 7)
ahol
I = biztonsági tényező
qa a megengedett teherbírás
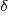a megengedett talajtelepülés
ezek az egyenletek egyértelműen jelzik, hogy a megfelelő biztonsági tényezőt kell használni, és a Ks érték jobban összehasonlítható a végső teherbírással, mint a megengedett teherbírással. A biztonsági tényező a projektektől és a geotechnikai mérnököktől függően változhat. A másik fontos tényező a számított teherbírás feltételezett megengedhető elszámolása.
hasonlóképpen meg kell jegyezni, hogy a FEA analízis által jelentett alapnyomás-értékek nem hasonlíthatók össze közvetlenül a teherbírással. A maximális alapnyomást meg kell szorozni a biztonsági tényezővel, majd össze kell hasonlítani a talaj megengedett teherbírásával.
a fent említett egyenleteknek azonban vannak korlátai. Alkalmazhatók olyan lábazatokra, ahol a kiegyenlítési hiba az irányadó, de nem kapcsolódhatnak olyan lábazatokhoz, ahol a nyírási hiba a megengedett kiegyenlítési határérték elérése előtt következik be. Tehát a mérnököknek óvatosan kell eljárniuk ezen egyenletek használata előtt.
következtetés
a teherbírás és a szubgrád reakció modulusa közötti korreláció legjobb esetben is csak becslés. Használható becsléshez, de a lemezterhelési teszttel meghatározott Ks értéket mindig használni kell, ha rendelkezésre áll, vagy amikor csak lehetséges, kérni kell. A fenti vita azonban betekintést nyújt ezekbe az értékekbe, és segít a mérnököknek megérteni a szubgrád reakció modulusának fizikai jelentőségét. És, mint mindig, a szerkezeti mérnököknek konzultálniuk kell egy Geotechnikai mérnök szakemberrel a talaj merevségének és a csapágyértékek véglegesítése előtt.▪