Householder Transformation
Householder Transformation (szintén “Householder Reflection”) egy ortogonális reflexiós transzformáció:
- a mátrix oszlopaiban lévő vektorokat úgy reflexeli, hogy
- az első vektornak az első elem kivételével minden nullája van
a transzformációs mátrix
reflexiós transzformáció:
tulajdonságok
a háztartási mátrixok szimmetrikusak és ortogonálisak: ezek reflexiós mátrixok
levezetés
tehát van $P = I-2VV^t$:
az ilyen transzformációkat az elemek nullázására használjuk
QR bomlás
mint az LU bomlás esetén, ahol Gauss-transzformációs változások sorozatát alkalmaztuk, ugyanezt megtehetjük és végrehajthatjuk a háztulajdonos-transzformációk sorozatát
- tehát, ha a $y = \pm e_1$ értéket választjuk (ahol $e_1$ az 1-es mátrix az 1-es pozícióban, a többi pedig nulla)
- akkor a $x$ összes elemét nullázza, kivéve az elsőt
- így a megfelelő választás $h$ tudjuk venni $a$ és nulla az összes Al-átlós elements
- lehet csinálni, hogy többször minden oszlop $A$
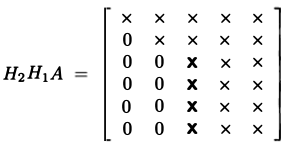
így tudjuk végrehajtani QR bomlás:
Hessenberg bomlás
ahelyett, hogy a mátrix háromszögre redukálására használnánk, használhatjuk háztulajdonos transzformáció hogy egy mátrixot Hessenberg mátrixra redukáljunk