Algoritmo Greedy con esempi: Metodo e approccio Greedy

Per comprendere l’approccio greedy, è necessario avere una conoscenza pratica della ricorsione e del cambio di contesto. Questo ti aiuta a capire come tracciare il codice. Puoi definire il paradigma greedy in termini di tue affermazioni necessarie e sufficienti.

Due condizioni definiscono il paradigma greedy.

• Ogni soluzione graduale deve strutturare un problema verso la soluzione più accettata.
• È sufficiente che la strutturazione del problema possa arrestarsi in un numero finito di passaggi avidi.

Con la teorizzazione continua, descriviamo la storia associata all’approccio di ricerca Greedy.

In questo tutorial algoritmo avido, si impara:

• Storia degli algoritmi Greedy
• Strategie e decisioni Greedy
• Caratteristiche dell’approccio Greedy
• Perché usare l’approccio Greedy?
• Come Risolvere l’attività di selezione del problema
• Architettura del Goloso approccio
• Svantaggi di Algoritmi Greedy

Storia di Algoritmi Greedy

Qui è un importante punto di riferimento di algoritmi greedy:

• gli algoritmi generici erano concettualizzato per molte grafico piedi algoritmi nel 1950.
• Esdger Djikstra concettualizzato l’algoritmo per generare il minimo che abbracciano gli alberi. Mirava ad accorciare l’arco delle rotte all’interno della capitale olandese, Amsterdam.
• Nello stesso decennio, Prim e Kruskal hanno raggiunto strategie di ottimizzazione basate sulla riduzione al minimo dei costi di percorso lungo le rotte pesate.
• Negli anni ‘ 70, ricercatori americani, Cormen, Rivest e Stein hanno proposto una sottostrutturazione ricorsiva di soluzioni avide nel loro libro di introduzione classica agli algoritmi.
• Il paradigma di ricerca Greedy è stato registrato come un diverso tipo di strategia di ottimizzazione nei record NIST nel 2005.
• Fino ad oggi, i protocolli che eseguono il web, come open-shortest-path-first (OSPF) e molti altri protocolli di commutazione di pacchetto di rete utilizzano la strategia greedy per ridurre al minimo il tempo trascorso su una rete.

Strategie e decisioni avide

La logica nella sua forma più semplice è stata ridotta a “avida” o “non avida”. Queste affermazioni sono state definite dall’approccio adottato per avanzare in ogni fase dell’algoritmo.

Ad esempio, l’algoritmo di Djikstra utilizzava una strategia avida graduale che identificava gli host su Internet calcolando una funzione di costo. Il valore restituito dalla funzione di costo determina se il percorso successivo è “greedy”o” non-greedy”.

In breve, un algoritmo cessa di essere avido se in qualsiasi fase prende un passo che non è localmente avido. I problemi avidi si fermano senza ulteriore portata di avidità.

Caratteristiche dell’approccio Greedy

Le caratteristiche importanti di un algoritmo di metodo Greedy sono:

• Esiste un elenco ordinato di risorse, con costi o attribuzioni di valore. Questi quantificano i vincoli su un sistema.
• Si prenderà la quantità massima di risorse nel tempo in cui si applica un vincolo.
• Ad esempio, in un problema di pianificazione delle attività, i costi delle risorse sono espressi in ore e le attività devono essere eseguite in ordine seriale.

Perché usare l’approccio avido?

Ecco i motivi per utilizzare l’approccio greedy:

• L’approccio greedy ha alcuni compromessi, che possono renderlo adatto per l’ottimizzazione.
• Un motivo importante è quello di ottenere immediatamente la soluzione più fattibile. Nel problema di selezione delle attività (spiegato di seguito), se è possibile eseguire più attività prima di terminare l’attività corrente, queste attività possono essere eseguite nello stesso tempo.
• Un altro motivo è quello di dividere un problema in modo ricorsivo in base a una condizione, senza la necessità di combinare tutte le soluzioni.
• Nel problema di selezione attività, la fase “divisione ricorsiva” viene eseguita scansionando un elenco di elementi una sola volta e considerando determinate attività.

Come risolvere il problema di selezione delle attività

Nell’esempio di pianificazione delle attività, c’è un tempo “start” e “finish” per ogni attività. Ogni Attività è indicizzata da un numero per riferimento. Ci sono due categorie di attività.

1. attività considerata: è l’Attività, che è il riferimento da cui viene analizzata la capacità di fare più di un’attività rimanente.
2. attività rimanenti: attività a uno o più indici prima dell’attività considerata.

La durata totale indica il costo di esecuzione dell’attività. Cioè (fine-inizio) ci dà la durata come il costo di un’attività.

Imparerai che l’estensione greedy è il numero di attività rimanenti che puoi eseguire nel tempo di un’attività considerata.

Architettura dell’approccio Greedy

PASSAGGIO 1)

Scansiona l’elenco dei costi di attività, iniziando con l’indice 0 come indice considerato.

PASSAGGIO 2)

Quando più attività possono essere terminate entro il tempo, l’attività considerata termina, avviare la ricerca di una o più attività rimanenti.

PASSAGGIO 3)

Se non ci sono più attività rimanenti, l’attività rimanente corrente diventa l’attività successiva considerata. Ripetere i passaggi 1 e 2, con la nuova attività considerata. Se non ci sono attività rimanenti, vai al passaggio 4.

PASSAGGIO 4)

Restituisce l’unione degli indici considerati. Questi sono gli indici di attività che verranno utilizzati per massimizzare il throughput.

Spiegazione del Codice

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

Spiegazione del codice:

1. Inclusi i file di intestazione/classi
2. Un numero massimo di attività previste dall’utente.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

Spiegazione del codice:

1. Lo spazio dei nomi per le operazioni di streaming.
2. Una definizione di classe per il TEMPO
3. Un timestamp ora.
4. Un costruttore predefinito di TEMPO
5. La variabile ore.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

Spiegazione del codice:

1. Una definizione di classe da attività di
2. Timestamp definizione di una durata
3. Tutti i timestamp sono inizializzati a 0 il costruttore di default

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

Spiegazione del codice:

1. Parte 1 di pianificazione definizione di classe.
2. L’indice considerato è il punto di partenza per la scansione dell’array.
3. L’indice di inizializzazione viene utilizzato per assegnare timestamp casuali.
4. Un array di oggetti attività viene allocato dinamicamente utilizzando il nuovo operatore.
5. Il puntatore pianificato definisce la posizione di base corrente per greed.

Scheduler(){ considered_index = 0; scheduled = NULL;......

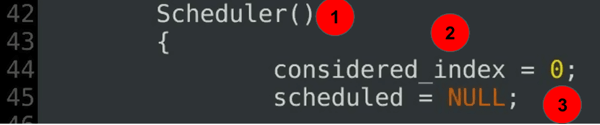
Spiegazione del codice:

1. Il costruttore scheduler-parte 2 della definizione della classe scheduler.
2. L’indice considerato definisce l’inizio corrente della scansione corrente.
3. L’attuale estensione greedy non è definita all’inizio.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

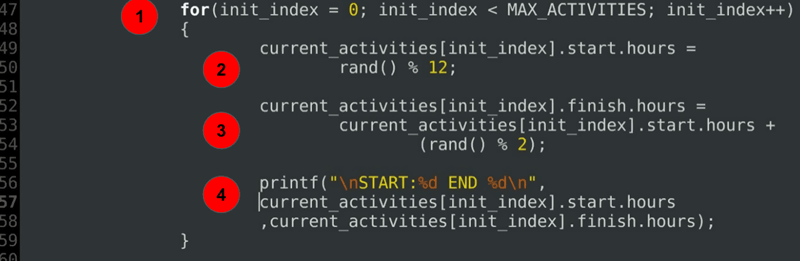
Spiegazione del codice:

1. Un ciclo for per inizializzare le ore di inizio e di fine di ciascuna delle attività attualmente pianificate.
2. Inizializzazione dell’ora di inizio.
3. Inizializzazione dell’ora di fine sempre dopo o esattamente all’ora di inizio.
4. Un’istruzione di debug per stampare le durate allocate.

public: Activity * activity_select(int);};

Spiegazione del codice:

1. Parte 4 – l’ultima parte della definizione della classe scheduler.
2. La funzione di selezione attività prende come base un indice del punto di partenza e divide la ricerca avida in sottoproblemi avidi.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. Utilizzando l’operatore di risoluzione dell’ambito (::), viene fornita la definizione della funzione.
2. L’indice considerato è l’indice chiamato per valore. greedy_extent è l’inizializzato solo un indice dopo l’indice considerato.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

Spiegazione del codice:

1. La logica di base-La misura avida è limitata al numero di attività.
2. Le ore di inizio dell’attività corrente vengono controllate come pianificabili prima che l’attività considerata (data dall’indice considerato) finisca.
3. Finché ciò è possibile, viene stampata un’istruzione di debug opzionale.
4. Passa all’indice successivo sull’array di attività

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

Spiegazione del codice:

1. I controlli condizionali se tutte le attività sono state coperte.
2. In caso contrario, è possibile riavviare il greedy con l’indice considerato come punto corrente. Questo è un passaggio ricorsivo che divide avidamente l’istruzione del problema.
3. Se sì, ritorna al chiamante senza possibilità di estendere l’avidità.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

Spiegazione del codice:

1. La funzione principale utilizzata per richiamare lo scheduler.
2. Viene istanziato un nuovo Scheduler.
3. La funzione activity select, che restituisce un puntatore di tipo activity, ritorna al chiamante al termine della ricerca avida.

Uscita:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

Svantaggi degli algoritmi Greedy

Non è adatto per problemi Greedy in cui è richiesta una soluzione per ogni sottoproblema come l’ordinamento.

In tali problemi di pratica dell’algoritmo Avido, il metodo Avido può essere sbagliato; nel peggiore dei casi persino portare a una soluzione non ottimale.

Quindi lo svantaggio degli algoritmi greedy sta usando non sapendo cosa ci aspetta rispetto all’attuale stato greedy.

Di seguito è riportata una rappresentazione dello svantaggio del metodo Greedy:

Nella scansione greedy mostrata qui come un albero (valore più alto maggiore avidità), uno stato dell’algoritmo al valore: 40, è probabile che prenda 29 come valore successivo. Inoltre, la sua ricerca termina a 12. Ciò equivale a un valore di 41.

Tuttavia, se l’algoritmo ha preso un percorso sub-ottimale o ha adottato una strategia di conquista. poi 25 sarebbe seguito da 40, e il miglioramento dei costi complessivi sarebbe 65, che è valutato 24 punti più alto come una decisione non ottimale.

Esempi di algoritmi Greedy

La maggior parte degli algoritmi di networking utilizza l’approccio greedy. Ecco un elenco di alcuni esempi di algoritmi avidi:

• Prim Minimo Algoritmo Spanning Tree
• Travelling Salesman Problem
• Grafico – Mappa da Colorare
• test di Kruskal Minimo Algoritmo Spanning Tree
• Dijkstra Minimo Algoritmo Spanning Tree
• Grafico – Vertex Cover
• Zaino Problema
• Lavoro Pianificazione Problema

Sintesi:

Per riassumere, l’articolo definito l’avido paradigma, ha mostrato come l’avido ottimizzazione e la ricorsione, può aiutare a ottenere la migliore soluzione fino a un certo punto. L’algoritmo Greedy è ampiamente preso in applicazione per la risoluzione dei problemi in molte lingue come algoritmo Greedy Python, C, C#, PHP,Java, ecc. L’esempio di selezione dell’attività dell’algoritmo Greedy è stato descritto come un problema strategico che potrebbe raggiungere il massimo throughput utilizzando l’approccio greedy. Alla fine, sono stati spiegati i demeriti dell’uso dell’approccio avido.