SSIM è stato introdotto per la prima volta nel documento IEEE del 2004, Image Quality Assessment: From Error Visibility to Structural Similarity. L’abstract fornisce una buona intuizione nell’idea alla base del sistema proposto,
I metodi oggettivi per la valutazione della qualità percettiva dell’immagine hanno tradizionalmente tentato di quantificare la visibilità degli errori (differenze) tra un’immagine distorta e un’immagine di riferimento utilizzando una varietà di proprietà note del sistema visivo umano. Partendo dal presupposto che la percezione visiva umana sia altamente adattata per estrarre informazioni strutturali da una scena, introduciamo un quadro complementare alternativo per la valutazione della qualità basato sul degrado delle informazioni strutturali.
Sommario: Gli autori fanno 2 punti essenziali,
- La maggior parte delle tecniche di valutazione della qualità dell’immagine si basa sulla quantificazione degli errori tra un’immagine di riferimento e un’immagine campione. Una metrica comune è quella di quantificare la differenza nei valori di ciascuno dei pixel corrispondenti tra il campione e le immagini di riferimento (utilizzando, ad esempio, Mean Squared Error).
- Il sistema di percezione visiva umana è altamente in grado di identificare le informazioni strutturali da una scena e quindi identificare le differenze tra le informazioni estratte da una scena di riferimento e una scena campione. Quindi, una metrica che replica questo comportamento funzionerà meglio sulle attività che comportano la differenziazione tra un campione e un’immagine di riferimento.
La Somiglianza Strutturale Indice (SSIM) metrica estratti 3 caratteristiche chiave da un’immagine:
- Luminanza
- Contrasto
- Struttura
Il confronto tra le due immagini è effettuata sulla base di queste 3 caratteristiche.
La figura 1 riportata di seguito mostra la disposizione e il flusso del sistema di misurazione della similarità strutturale. Il segnale X e il segnale Y si riferiscono alle immagini di riferimento e campione.

Ma cosa calcola questa metrica?
Questo sistema calcola l’indice di somiglianza strutturale tra 2 immagini date che è un valore compreso tra -1 e + 1. Un valore di +1 indica che le 2 immagini date sono molto simili o uguali mentre un valore di -1 indica che le 2 immagini date sono molto diverse. Spesso questi valori sono regolati per essere nell’intervallo , dove gli estremi hanno lo stesso significato.
Ora, esploriamo brevemente, come queste caratteristiche sono rappresentate matematicamente e come contribuiscono al punteggio SSIM finale.
- Luminanza: la luminanza viene misurata facendo una media su tutti i valori dei pixel. È indicato da μ (Mu) e la formula è riportata di seguito,
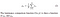
- Contrasto: Si misura prendendo la deviazione standard (radice quadrata della varianza) di tutti i valori dei pixel. Esso è indicato con s (sigma) e rappresentato dalla seguente formula,
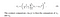
- Struttura: Il confronto strutturale viene fatto utilizzando una formula consolidata (ne parleremo più avanti) ma in sostanza, dividiamo il segnale di ingresso con la sua deviazione standard in modo che il risultato abbia una deviazione standard unitaria che consente un confronto più robusto.
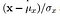
Così ora abbiamo stabilito l’intuizione matematica dietro i tre parametri. Ma resisti! Non abbiamo ancora finito con la matematica, un po ‘ di più. Quello che ci manca ora, sono funzioni di confronto che possono confrontare le due immagini date su questi parametri, e, infine, una funzione di combinazione che li combina tutti. Qui, definiamo le funzioni di confronto e infine la funzione di combinazione che produce il valore dell’indice di somiglianza
- Funzione di confronto della luminanza: è definita da una funzione, l(x, y) che è mostrata sotto. μ (mu) rappresenta la media di una data immagine. x e y sono le due immagini che vengono confrontate.
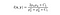
dove C1 è una costante per garantire stabilità quando il denominatore diventa 0. C1 è dato da,
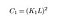
Aggiornamento: In tutto l’articolo, non avevamo esplorato quali siano le costanti K e L in questa equazione. Per fortuna un lettore lo ha sottolineato nei commenti, e quindi nell’interesse di rendere questo articolo un po ‘ più utile, li definirò qui.
L è l’intervallo dinamico per i valori dei pixel (lo impostiamo come 255 poiché abbiamo a che fare con immagini standard a 8 bit). Puoi leggere di più su quali sono i diversi tipi di immagine e cosa significano, qui.
K1, K2 sono solo costanti normali, niente di molto lì!
- Funzione di confronto del contrasto: è definita da una funzione c (x, y) che viene mostrata di seguito. σ indica la deviazione standard di una data immagine. x e y sono le due immagini che vengono confrontate.
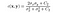
dove C2 è dato da,
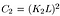
- Struttura, funzione di confronto: Esso è definito dalla funzione s(x, y) che è riportato di seguito. σ indica la deviazione standard di una data immagine. x e y sono le due immagini che vengono confrontate.
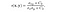
dove σ(xy) è definito come,
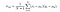
E, infine, il SSIM punteggio è dato da,

dove α > 0, β > 0, γ > 0 denotano l’importanza relativa di ciascuna delle metriche. Per semplificare l’espressione, se assumiamo, α = β = γ = 1 e C3 = C2 / 2, possiamo ottenere,
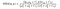
Ma c’è un colpo di scena!
Mentre si sarebbe in grado di implementare SSIM utilizzando le formule di cui sopra, è probabile che non sarà buono come le implementazioni pronte all’uso disponibili, come spiegano gli autori,
Per la valutazione della qualità dell’immagine, è utile applicare l’indice SSIM localmente anziché globalmente. In primo luogo, le caratteristiche statistiche dell’immagine sono di solito altamente spazialmente non stazionarie. In secondo luogo, le distorsioni dell’immagine, che possono o non possono dipendere dalle statistiche locali dell’immagine, possono anche essere varianti dello spazio. In terzo luogo, a distanze di visione tipiche, solo un’area locale nell’immagine può essere percepita con alta risoluzione dall’osservatore umano in un’unica istanza (a causa della caratteristica di foveation dell’HVS ). Infine, la misurazione della qualità localizzata può fornire una mappa di qualità spazialmente variabile dell’immagine, che fornisce ulteriori informazioni sul degrado della qualità dell’immagine e può essere utile in alcune applicazioni.
Sommario: Invece di applicare le metriche di cui sopra a livello globale (cioè su tutta l’immagine in una sola volta) è meglio applicare le metriche a livello regionale (cioè in piccole sezioni dell’immagine e prendendo la media complessiva).
Questo metodo è spesso indicato come Indice di somiglianza strutturale media.
A causa di questo cambiamento di approccio, le nostre formule meritano anche modifiche per riflettere lo stesso (va notato che questo approccio è più comune e verrà utilizzato per spiegare il codice).
(Nota: se il contenuto qui sotto sembra un po ‘ opprimente, non preoccuparti! Se ne ottieni il succo, passare attraverso il codice ti darà un’idea molto più chiara.)
Gli autori usano una funzione di pesatura gaussiana circolare-simmetrica 11×11 (fondamentalmente, una matrice 11×11 i cui valori sono derivati da una distribuzione gaussiana) che si muove pixel per pixel sull’intera immagine. Ad ogni passaggio, le statistiche locali e l’indice SSIM vengono calcolati all’interno della finestra locale. Poiché ora stiamo calcolando le metriche localmente, le nostre formule vengono riviste come,
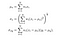
Dove wi è la funzione di ponderazione gaussiana.
Se hai trovato questo un po ‘ poco intuitivo, non preoccuparti! Basta immaginare wi come un moltiplicoe che viene utilizzato per calcolare i valori richiesti con l’aiuto di alcuni trucchi matematici.
Una volta che i calcoli vengono eseguiti su tutta l’immagine, prendiamo semplicemente la media di tutti i valori SSIM locali e arriviamo al valore SSIM globale.
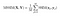
Finalmente fatto con la teoria! Ora sul codice!