Il campo elettrico E può sempre essere espresso come il gradiente di un potenziale scalare funzione
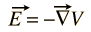
non C’è scalare potenziale per il campo magnetico B, ma può essere espresso come il riccio di una funzione vettoriale
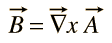
Questa funzione è dato il nome di “vettore potenziale”, ma non è direttamente associato con il lavoro, il modo in cui scalare potenziale.
Il potenziale vettoriale è definito per essere coerente con la Legge di Ampere e può essere espresso in termini di corrente i o densità di corrente j (le sorgenti del campo magnetico). In vari testi questa definizione assume le forme
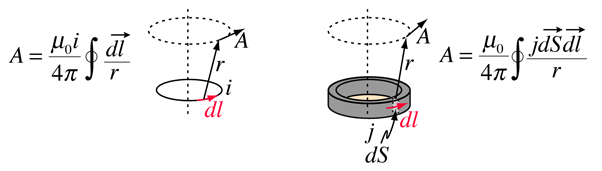
Una logica per il potenziale vettoriale è che potrebbe essere più facile calcolare il potenziale vettoriale che calcolare il campo magnetico direttamente da una data geometria della corrente di sorgente. La sua applicazione più comune è la teoria dell’antenna e la descrizione delle onde elettromagnetiche.
Poiché il campo magnetico B è definito come il ricciolo di A e l’identità vettoriale il ricciolo di un gradiente è identicamente zero, allora qualsiasi funzione arbitraria che può essere espressa come il gradiente di una funzione scalare può essere aggiunta ad A senza modificare il valore di B ottenuto da esso. Cioè, A ‘ può essere liberamente sostituito da Un dove
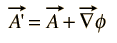
Tali trasformazioni sono chiamate trasformazioni di gauge, e ci sono stati un certo numero di “calibri” che sono stati utilizzati a vantaggio è tipi specifici di calcoli in teoria elettromagnetica.