Ricottura simulata per principianti

Trovare una soluzione ottimale per alcuni problemi di ottimizzazione può essere un compito incredibilmente difficile, spesso praticamente impossibile. Questo perché quando un problema diventa sufficientemente grande abbiamo bisogno di cercare attraverso un numero enorme di possibili soluzioni per trovare quello ottimale. Anche con la moderna potenza di calcolo ci sono ancora spesso troppe possibili soluzioni da considerare. In questo caso, poiché non possiamo realisticamente aspettarci di trovare quello ottimale in un lasso di tempo ragionevole, dobbiamo accontentarci di qualcosa che sia abbastanza vicino.
Un problema di ottimizzazione di esempio che di solito ha un gran numero di possibili soluzioni sarebbe il problema del commesso viaggiatore. Per trovare una soluzione a un problema come il problema del commesso viaggiatore, dobbiamo utilizzare un algoritmo in grado di trovare una soluzione abbastanza buona in un ragionevole lasso di tempo. In un precedente tutorial abbiamo esaminato come potremmo farlo con algoritmi genetici, e anche se gli algoritmi genetici sono un modo in cui possiamo trovare una soluzione “abbastanza buona” al problema del commesso viaggiatore, ci sono altri algoritmi più semplici che possiamo implementare che ci troveranno anche una soluzione vicina a quella ottimale. In questo tutorial l’algoritmo che useremo è, ‘ricottura simulata’.
Se non hai familiarità con il problema del commesso viaggiatore, potrebbe valere la pena dare un’occhiata al mio precedente tutorial prima di continuare.

Che cos’è la ricottura simulata?

In primo luogo, diamo un’occhiata a come funziona la ricottura simulata e perché è bravo a trovare soluzioni al problema del commesso viaggiatore in particolare. L’algoritmo di ricottura simulato è stato originariamente ispirato dal processo di ricottura nella lavorazione dei metalli. La ricottura comporta il riscaldamento e il raffreddamento di un materiale per alterare le sue proprietà fisiche a causa dei cambiamenti nella sua struttura interna. Quando il metallo si raffredda, la sua nuova struttura diventa fissa, causando di conseguenza il metallo a mantenere le sue proprietà appena ottenute. Nella ricottura simulata manteniamo una variabile di temperatura per simulare questo processo di riscaldamento. Inizialmente lo impostiamo in alto e poi lo lasciamo lentamente “raffreddare” mentre l’algoritmo viene eseguito. Mentre questa variabile di temperatura è alta, l’algoritmo sarà autorizzato, con più frequenza, ad accettare soluzioni peggiori della nostra soluzione attuale. Ciò dà all’algoritmo la possibilità di saltare fuori da qualsiasi optimum locale in cui si trova all’inizio dell’esecuzione. Come la temperatura è ridotta così è la possibilità di accettare soluzioni peggiori, consentendo quindi l’algoritmo di concentrarsi gradualmente in una zona dello spazio di ricerca in cui si spera, una soluzione vicina a ottimale può essere trovato. Questo processo di “raffreddamento” graduale è ciò che rende l’algoritmo di ricottura simulato straordinariamente efficace nel trovare una soluzione quasi ottimale quando si affrontano problemi di grandi dimensioni che contengono numerosi ottimismi locali. La natura del problema del commesso viaggiatore lo rende un esempio perfetto.

Vantaggi della ricottura simulata

Ci si potrebbe chiedere se ci sia un reale vantaggio nell’implementazione della ricottura simulata su qualcosa come un semplice scalatore. Anche se gli alpinisti possono essere sorprendentemente efficaci nel trovare una buona soluzione, hanno anche la tendenza a rimanere bloccati in optimum locali. Come abbiamo precedentemente determinato, l’algoritmo di ricottura simulato è eccellente per evitare questo problema ed è molto meglio in media a trovare un ottimale globale approssimativo.
Per aiutare a capire meglio diamo rapidamente un’occhiata al motivo per cui un algoritmo di arrampicata in collina di base è così incline a rimanere intrappolati in optimum locali.
Un algoritmo hill climber accetterà semplicemente soluzioni vicine che sono migliori della soluzione attuale. Quando l’alpinista non riesce a trovare vicini migliori, si ferma.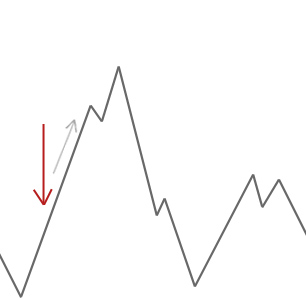

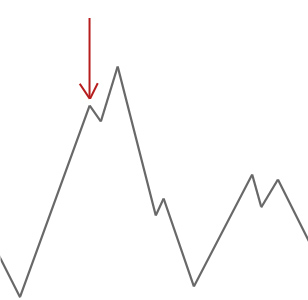
Nell’esempio sopra iniziamo il nostro alpinista alla freccia rossa e si fa strada fino a raggiungere un punto in cui non può salire più in alto senza prima scendere. In questo esempio possiamo vedere chiaramente che è bloccato in un ottimale locale. Se questo fosse un problema del mondo reale, non sapremmo come appare lo spazio di ricerca, quindi sfortunatamente non saremmo in grado di dire se questa soluzione è da nessuna parte vicina a un optimum globale.
La ricottura simulata funziona in modo leggermente diverso da questo e occasionalmente accetta soluzioni peggiori. Questa caratteristica della ricottura simulata lo aiuta a saltare fuori da qualsiasi optimum locale in cui potrebbe essere rimasto bloccato.

Funzione di accettazione

Diamo un’occhiata a come l’algoritmo decide quali soluzioni accettare in modo da poter capire meglio come è in grado di evitare questi ottimismi locali.
Per prima cosa controlliamo se la soluzione vicina è migliore della nostra soluzione attuale. Se lo è, lo accettiamo incondizionatamente. Se, tuttavia, la soluzione vicina non è migliore, dobbiamo considerare un paio di fattori. In primo luogo, quanto è peggiore la soluzione vicina; e in secondo luogo, quanto è alta l’attuale “temperatura” del nostro sistema. Alle alte temperature il sistema è più probabile accettare soluzioni che sono peggiori.
La matematica per questo è piuttosto semplice:

Fondamentalmente, minore è il cambiamento di energia (la qualità della soluzione) e maggiore è la temperatura, più è probabile che l’algoritmo accetti la soluzione.

Panoramica dell’algoritmo

Quindi, come appare l’algoritmo? Bene, nella sua implementazione più elementare è piuttosto semplice.

• Per prima cosa dobbiamo impostare la temperatura iniziale e creare una soluzione iniziale casuale.
• Quindi iniziamo il loop fino a quando la nostra condizione di stop non è soddisfatta. Di solito il sistema si è sufficientemente raffreddato o è stata trovata una soluzione abbastanza buona.
• Da qui selezioniamo un vicino apportando una piccola modifica alla nostra soluzione attuale.
• Decidiamo quindi se passare a quella soluzione vicina.
• Infine, diminuiamo la temperatura e continuiamo il loop

Inizializzazione della temperatura

Per una migliore ottimizzazione, quando inizializziamo la variabile di temperatura dovremmo selezionare una temperatura che inizialmente consenta praticamente qualsiasi movimento contro la soluzione corrente. Questo dà l’algoritmo la possibilità di esplorare meglio l’intero spazio di ricerca prima di raffreddamento e stabilirsi in una regione più focalizzata.

Codice di esempio

Ora usiamo ciò che sappiamo per creare un algoritmo di ricottura simulato di base e quindi applicarlo al problema del venditore ambulante di seguito. Useremo Java in questo tutorial, ma la logica dovrebbe essere abbastanza semplice da copiare in qualsiasi lingua di tua scelta.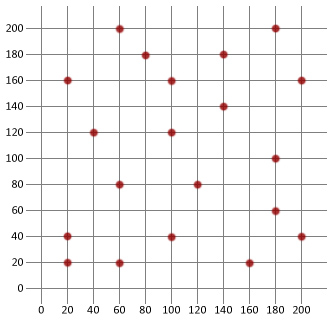

Per prima cosa dobbiamo creare una classe di città che possa essere utilizzata per modellare le diverse destinazioni del nostro venditore ambulante.
Città.java

Quindi creiamo una classe che può tenere traccia delle città.
TourManager.java

Ora per creare la classe che può modellare un tour venditore itinerante.
Giro.java

Infine, creiamo il nostro algoritmo di ricottura simulato.
SimulatedAnnealing.java

di Uscita

Conclusione

In questo esempio siamo stati in grado di più di metà della distanza iniziale generato in modo casuale del percorso. Si spera che questo mostri quanto sia utile questo algoritmo relativamente semplice quando applicato a determinati tipi di problemi di ottimizzazione.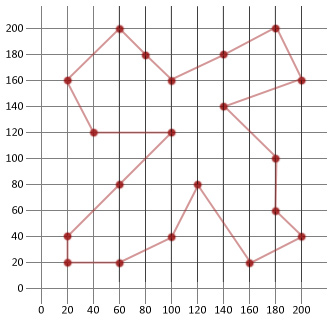

Autore

Ciao, sono Lee.
Sono uno sviluppatore dal Regno Unito che ama la tecnologia e il business. Qui troverete articoli e tutorial su cose che mi interessano. Se vuoi assumermi o saperne di più su di me vai alla mia pagina su di me