Ho iniziato a fare il popolare corso di apprendimento automatico di Andrew Ng su Coursera. La prima settimana copre molto, almeno per qualcuno che non ha toccato molto calcolo per alcuni anni
- Funzioni di costo (differenza media al quadrato)
- Discesa del gradiente
- Regressione lineare
Questi tre argomenti erano molto da prendere in considerazione. Parlerò di ciascuno in dettaglio e di come si adattano tutti insieme, con un codice python da dimostrare.
Modifica 4 maggio: Ho pubblicato un follow-up incentrato su come funziona la funzione di costo qui, tra cui un’intuizione, come calcolarlo a mano e due diverse implementazioni Python. Posso fare la discesa del gradiente e poi riunirli presto per la regressione lineare.
Rappresentazione del modello
In primo luogo, l’obiettivo della maggior parte degli algoritmi di apprendimento automatico è quello di costruire un modello: un’ipotesi che può essere utilizzata per stimare Y in base a X. L’ipotesi, o modello, mappa gli input agli output. Quindi, per esempio, diciamo che alleno un modello basato su una serie di dati abitativi che includono le dimensioni della casa e il prezzo di vendita. Allenando un modello, posso darti una stima su quanto puoi vendere la tua casa in base alle sue dimensioni. Questo è un esempio di un problema di regressione — dato qualche input, vogliamo prevedere un output continuo.
L’ipotesi è solitamente presentata come

I valori theta sono i parametri.
Alcuni rapidi esempi di come visualizziamo l’ipotesi:
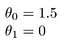
Questo produce h (x) = 1,5 + 0x. 0x significa nessuna pendenza e y sarà sempre la costante 1.5. Questo appare come:

Come
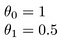

L’obiettivo di creare un modello è quello di scegliere i parametri o i valori di theta, in modo che h(x) è vicino a y per la formazione dei dati, x e y. Quindi per questi dati
x =
y =

Cercherò di trovare una linea di adattamento migliore usando la regressione lineare. Cominciamo.
Funzione di costo
Abbiamo bisogno di una funzione che minimizzi i parametri sul nostro set di dati. Una funzione comune che viene spesso utilizzata è mean squared error, che misura la differenza tra lo stimatore (il set di dati) e il valore stimato (la previsione). Sembra questo:

Si scopre che possiamo regolare l’equazione un po ‘per rendere il calcolo lungo la pista un po’ più semplice. Si finisce con l’:
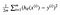
proviamo ad applicare questo const funzione a seguire i dati:

Per ora possiamo calcolare i valori di theta, e la trama la funzione di costo a mano. Poiché questa funzione passa attraverso (0, 0), stiamo solo guardando un singolo valore di theta. Da qui in poi, mi riferirò alla funzione di costo come J (Θ).
Per J(1), otteniamo 0. Nessuna sorpresa: un valore di J(1) produce una linea retta che si adatta perfettamente ai dati. Che ne dici di J (0.5)?

La funzione MSE ci dà un valore di 0.58. Tracciamo entrambi i nostri valori finora:
J(1) = 0
J (0,5) = 0.58

Andrò avanti e calcolerò altri valori di J (Θ).

E se uniamo i puntini bene insieme…

Possiamo vedere che la funzione di costo è minima quando theta = 1. Questo ha senso: i nostri dati iniziali sono una linea retta con una pendenza di 1 (la linea arancione nella figura sopra).
Discesa del gradiente
Abbiamo ridotto al minimo J(Θ) per tentativi ed errori sopra — solo provando molti valori e ispezionando visivamente il grafico risultante. Ci deve essere un modo migliore? Discesa del gradiente di coda. La discesa del gradiente è una funzione generale per ridurre al minimo una funzione, in questo caso la funzione di costo dell’errore quadrato medio.
La discesa del gradiente fondamentalmente fa solo quello che stavamo facendo a mano — cambia i valori theta, oi parametri, a poco a poco, fino a quando speriamo di arrivare al minimo.
Iniziamo inizializzando theta0 e theta1 a due valori qualsiasi, diciamo 0 per entrambi, e andiamo da lì. Formalmente, l’algoritmo è il seguente:

dove α, alfa, è il tasso di apprendimento, o quanto velocemente si desidera spostare verso il minimo. Se α è troppo grande, tuttavia, possiamo oltrepassare.

Portare tutto insieme — Regressione Lineare
riassumere Rapidamente:
Abbiamo un ipotesi:

che abbiamo bisogno di adattarsi al nostro allenamento. Possiamo usare una funzione di costo tale errore quadrato medio:

che siamo in grado di ridurre al minimo con gradiente di discesa:

Che ci conduce alla nostra prima macchina algoritmo di apprendimento, di regressione lineare. L’ultimo pezzo del puzzle che dobbiamo risolvere per avere un modello di regressione lineare funzionante è la derivata parziale della funzione costo:
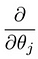
Che risulta essere di:
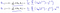
Che ci dà la regressione lineare!
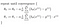
Con la teoria fuori mano, continuerò a implementare questa logica in python nel prossimo post.
Modifica 4 maggio: ho pubblicato un follow-up incentrato su come funziona la funzione di costo qui, tra cui un’intuizione, come calcolarlo a mano e due diverse implementazioni Python. Posso fare la discesa del gradiente e poi riunirli presto per la regressione lineare.