Simplifying FEA Models: Plane Stress and Plane Strain

Nota del redattore: Tony Abbey insegna lezioni NAFEMS FEA dal vivo negli Stati Uniti, in Europa e in Asia. Insegna anche lezioni di e-learning NAFEMS a livello globale. Contatto .per i dettagli.

Un precedente articolo di Desktop Engineering (“Simplify FEA Simulation Models Using Planar Symmetry”) ha spiegato che anche con potenti computer moderni, c’è spesso una motivazione per utilizzare tecniche di semplificazione nell’analisi strutturale degli elementi finiti (FEA). Questo follow-up descrive come due metodi strettamente correlati possono essere utilizzati per prendere fette 2D attraverso una struttura complessa a regioni di interesse. I modelli FEA risultanti possono fornire informazioni preziose sulle sollecitazioni locali in modo più rapido ed efficiente rispetto a un modello 3D completo. Non racconteranno tutta la storia, ma sono strumenti preziosi per l’ingegnere CAE.

I due metodi FEA sono chiamati sforzo piano e sforzo piano. Entrambi utilizzano elementi planari 2D che assomigliano a elementi di shell sottili e sono ingranati utilizzando la geometria della superficie planare.

Analisi delle sollecitazioni piane

Fig. 1 mostra i fatti importanti sull’analisi dello stress aereo. Si presume che la regione strutturale si trovi nel piano 2D xy, con la terza dimensione strutturale relativamente piccola. Nella figura, questo è lo spessore nella direzione z. Le sollecitazioni esistono nel piano 2D come sigma x, sigma y (sollecitazioni dirette) e sigma xy (stress di taglio in-plane). Ciascuna di queste sollecitazioni è costante attraverso lo spessore come mostrato nell’inserto. Inoltre non ci può essere stress nella direzione Z. Questa relazione materiale sforzo-deformazione è definita negli elementi di stress piano 2D utilizzati in questo tipo di analisi.

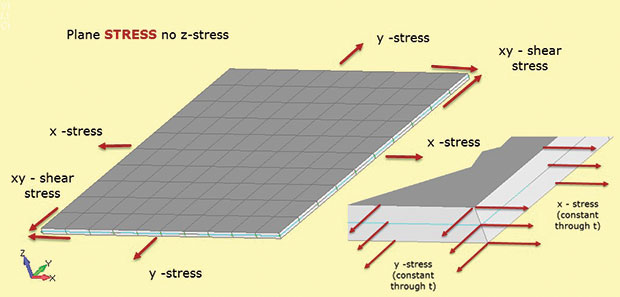Fig. 1: Stress piano; ipotesi dello stato di stress.

La mancanza di stress z è il modo per ricordare lo stress piano di designazione del tipo di elemento (cioè solo le sollecitazioni in piano consentite). Non ci sono inoltre sollecitazioni di taglio attraverso lo spessore. Potremmo caricare il modello di stress aereo in Fig. 1 con un carico biassiale e calcolare sigma x e sigma y. Non c’è sigma z. Possiamo anche calcolare i corrispondenti ceppi in-plane e-x ed e-y. Se applichiamo un carico di taglio, possiamo trovare lo stress di taglio sigma xy e lo sforzo di taglio e-xy. È interessante notare che possiamo anche calcolare la deformazione dello spessore passante ez. Questo non è zero, poiché il modello è libero di assottigliarsi in z mentre si estende in x e y. Non esiste un vincolo fuori piano per impedirlo. In alcuni risolutori possiamo recuperare il ceppo di spessore passante ez e usarlo per calcolare la variazione di spessore. (Se il modello è in compressione biassiale, la sezione z diventerà più spessa). Questo di solito è considerato un ceppo secondario e potrebbe non essere disponibile per l’output, ma è lì e può essere calcolato manualmente se necessario.

Fig. 2 mostra un componente aletta in alluminio. L’aletta sporge da un layup foglio composito che ha strati posizionati e legati sopra le linguette (o gambe) e sezione inferiore del corpo. Le linguette trasferiscono il carico applicato all’aletta nella struttura composita. In pratica, gli strati sarebbero fatti un passo per consentire un trasferimento di taglio liscio attraverso il legame nel composito. Il trasferimento di taglio nel composito è simulato qui da forze di trazione superficiali diffuse che “tirano” sulle linguette. Questi bilanciano il carico aletta applicato.

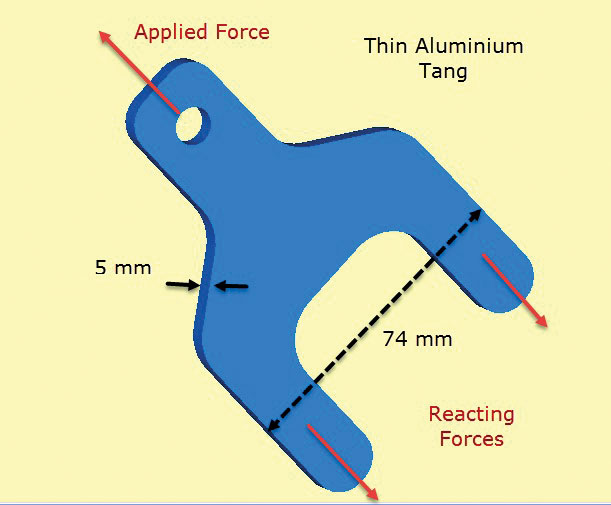Fig. 2: Tang in alluminio a parete sottile che trasferisce il carico nella struttura composita.

L’ipotesi chiave qui è che attraverso le sollecitazioni di spessore sono zero e le sollecitazioni in-plane sono costanti attraverso lo spessore nel componente. Ciò significa che il dettaglio locale del trasferimento del carico di taglio dal composito al codolo è scarsamente modellato. Tuttavia, l’obiettivo di questa analisi è quello di verificare il dimensionamento della sezione trasversale di lug e tang libera dal composito, utilizzando sollecitazioni in-plane.

Lo spessore del componente è ridotto rispetto ad altre dimensioni. Questo valore viene immesso come spessore effettivo nella definizione dell’elemento di sollecitazione del piano.

Fig. 3 mostra il modello FEA e le tensioni principali massime calcolate. Le aree di interesse sono intorno all’aletta e ai raggi della spalla. Nel mondo reale lo stato di stress alle concentrazioni di stress sarebbe 3D e attraverso lo spessore le sollecitazioni sigma z e le sollecitazioni di taglio si equilibrerebbero localmente. Tuttavia, è molto ragionevole qui assumere che le sollecitazioni in-plane dominino. Questa è la stessa ipotesi implicita nella maggior parte dei calcoli tradizionali di concentrazione dello stress (Kt) trovati nei manuali.

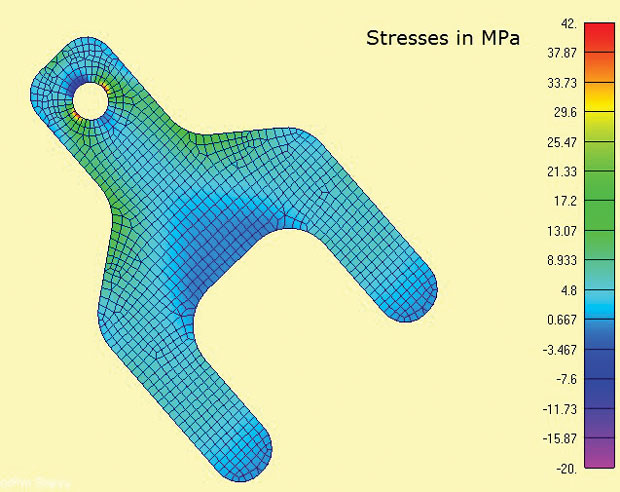Fig 3: Elementi di stress piano 2D che mostrano le massime sollecitazioni principali

Una delle caratteristiche utili dell’analisi di stress piano è che è un’analisi strettamente 2D, quindi solo tre gradi di libertà (DOF) devono essere vincolati (traduzioni in piano x, y e rotazione sull’asse z). Questo si presta al metodo di vincolo minimo 3-2-1 con carico bilanciato. In un caso 2D questo degenera in un metodo 2-1. Un nodo ha DOF x e y vincolato, un secondo nodo ortogonale appropriato ha DOF x vincolato. Ciò consente di applicare direttamente il carico di reazione nei codoli come carichi di bilanciamento diffusi. Sarebbe difficile simulare questa condizione al contorno tramite vincoli a terra.

Lo spessore passante e-z e quindi l’assottigliamento dei codoli potrebbero essere calcolati come effetto secondario.

Analisi della deformazione piana

Fig. 4 mostra l’essenza del metodo di deformazione piana. Ancora una volta, vengono utilizzati elementi planari 2D, ma con ipotesi sottilmente diverse. Le sollecitazioni in piano x, y e xy sono sviluppate come prima. Tuttavia questa volta è il ceppo out-of-plane, o attraverso lo spessore z che è impostato su zero. Quindi l’analisi della deformazione piana consente solo ceppi in piano. Questo funziona bene per rappresentare strutture spesse come mostrato. La presenza di questo materiale tende a stabilizzare il componente e ad impedirne lo sforzo in z. Ciò significa anche che nella struttura si sviluppano tensioni z costanti attraverso lo spessore. Questa relazione materiale sforzo-deformazione è definita negli elementi di deformazione piana 2D utilizzati in questo tipo di analisi.

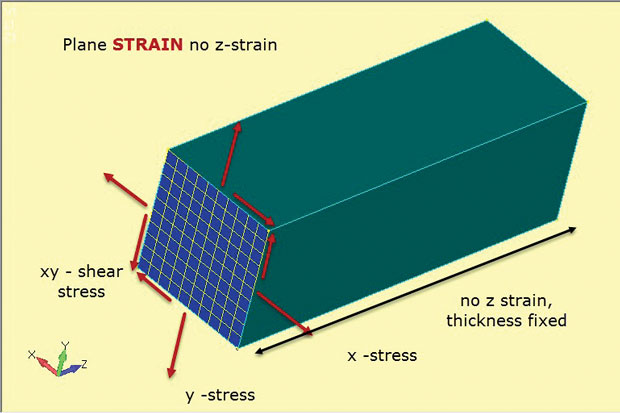Fig. 4: Analisi della deformazione piana; ipotesi di stress e stato di deformazione.

La figura mostra l’orientamento degli elementi di deformazione del piano 2D come una sezione di taglio attraverso un tipico componente profondo. L’ipotesi è che lo stato di stress in questa sezione di taglio verrà duplicato in qualsiasi taglio piano xy (stazione z) attraverso il componente. Si presume che il componente sia prismatico (con una sezione trasversale costante) lungo la sua lunghezza.

In pratica usiamo questo metodo in cui lo stato di stress varia lentamente da un piano all’altro in una componente profonda. Ci dovrebbe essere abbastanza materiale attraverso la profondità per stabilizzare ed eliminare lo sforzo di spessore passante. Questo è lo stesso principio utilizzato su campioni di resistenza alla frattura mostrato in Fig. 5. Un guasto nelle circostanze piane di sforzo è indicato per la sezione centrale dell’esemplare spesso. Il guasto ai bordi liberi e alla sezione sottile è una modalità diversa, più simile a uno stato di stress aereo. Un modello FEA di deformazione piana sarebbe per definizione una buona rappresentazione del comportamento del campione spesso della linea centrale, ma non dei bordi liberi o del campione sottile.

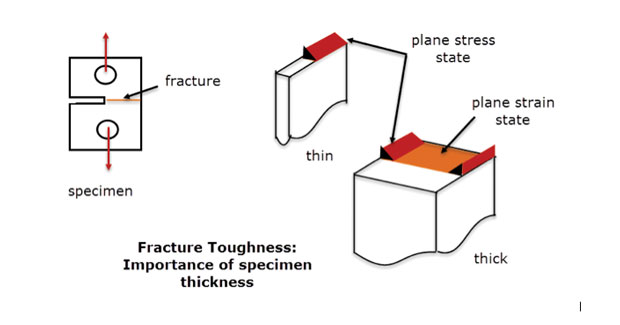Fig. 5: Campioni di tenacità alla frattura; sezioni sottili e spesse.

Fig. 6 mostra un altro componente utilizzato in una struttura composita, formando un giunto incollato. Qui la sezione è costante e abbastanza profonda da poter supporre che anche le sollecitazioni siano costanti con la profondità. Le facce della superficie finale libera (a + z, – z) avranno uno stato di stress locale diverso (in realtà lo stress piano, come notato), tuttavia l’obiettivo di questa analisi è quello di controllare le tensioni di sezione netta sulla linea centrale (z = 0).

La maglia di analisi della deformazione piana 2D è mostrata sezionata nel componente 3D in Fig. 7. Il taglio di sezione è definito alla stazione z = 0.

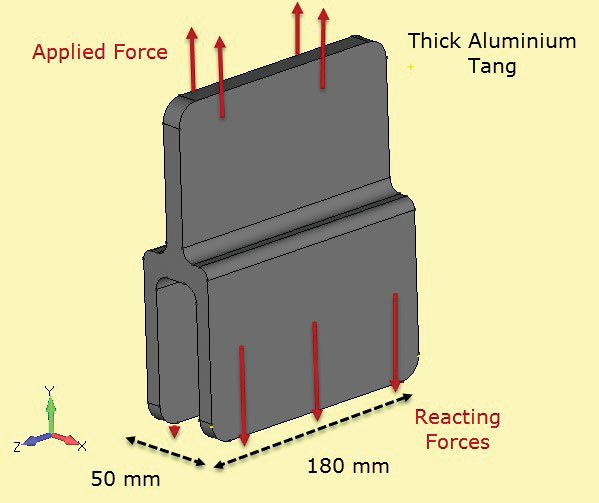Fig 6: Codolo in alluminio a sezione profonda.

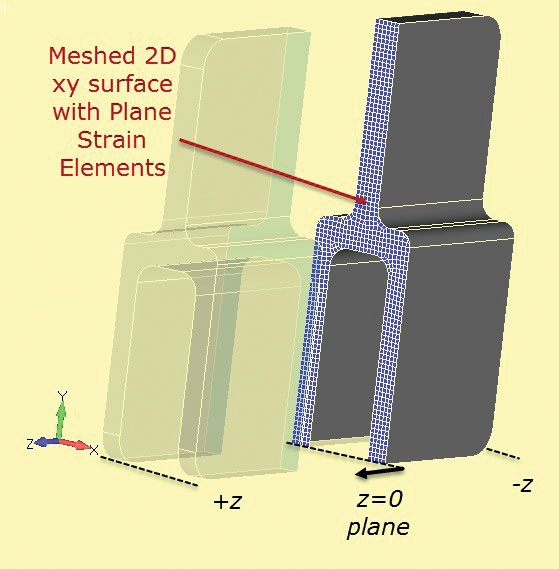Fig. 7: Sezione tagliare la sezione solida per sviluppare la sezione di deformazione piana 2D.

È possibile utilizzare una rete di deformazione piana 2D molto fine, che verrà eseguita molto rapidamente rispetto a un modello 3D completo. Il metodo di vincolo 2-1 viene utilizzato come prima. Il carico deve essere considerato attentamente. Lo “spessore” della sezione di deformazione piana è abbastanza arbitrario e di solito è impostato su 1.0 per impostazione predefinita. Se il carico sul componente è calcolato come un carico in esecuzione attraverso la profondità (N/m, Lbf/inch ecc.) quindi questo valore può essere utilizzato direttamente sulla rete di deformazione piana. È utile scegliere una sezione, come il singolo codolo e stimare la sollecitazione nominale o media in questa sezione per il componente completo. Questo può essere usato come controllo di sanità mentale nell’analisi del ceppo aereo. Il caricamento errato è probabilmente la causa principale di errore in questo metodo.

I risultati dell’analisi sono mostrati in Fig. 8 e mostrare chiaramente le regioni di alto stress intorno al filetto di spalla. Le sollecitazioni sono valide per la regione di profondità centrale del componente (z = 0).

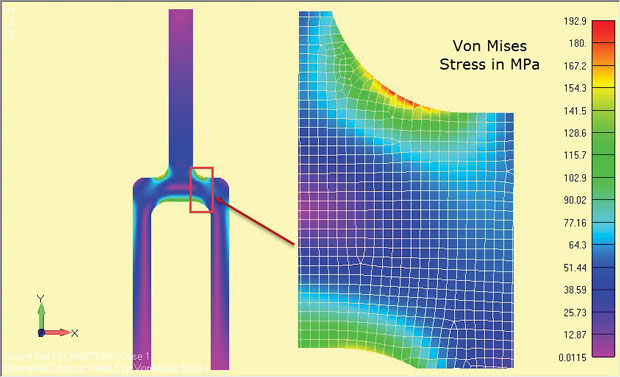Fig. 8: Risultati dell’analisi della deformazione piana di un componente tang profondo.

Le quantità di stress utilizzate dipenderanno dal risolutore utilizzato. Alcuni risolutori ignorano le sollecitazioni di direzione z come secondarie e recuperano le sollecitazioni in piano. Gli stress principali e gli stress di von Mises si riferiscono quindi a uno stato di stress in-plane 2D. Se lo stress di direzione z viene recuperato, dovrebbe essere chiaramente identificato, in modo che lo stato di stress 2D nel piano XY possa essere identificato.

Che cosa rappresenta esattamente lo stress della direzione z? È lo sforzo sviluppato dovuto l’applicazione dello sforzo zero di direzione di Z. Lo stress agisce come se le facce terminali libere della sezione prismatica fossero fisse. Al piano centrale di un componente di sezione profonda queste saranno le sollecitazioni complementari necessarie per mantenere lo stato di deformazione in direzione z zero. In realtà, mentre ci spostiamo verso le facce della superficie libera, lo stress z scende a zero e diventa una distribuzione dello stress piano (come si vede nel campione di meccanica della frattura spessa).

In molti casi, come un cilindro pressurizzato, le facce terminali sono tappate e di fatto sviluppano una sollecitazione assiale dovuta alle forze assiali. Questa sarà una sollecitazione diversa dalla sollecitazione assiale indotta nell’analisi della deformazione piana. Sarà necessario un calcolo manuale per calcolare le sollecitazioni assiali, o possibile un modello assisimmetrico supplementare per recipienti a pressione.

La facilità di geometria e costruzione della maglia si presta bene a studi “what-if” o studi di ottimizzazione della forma più formali.

Per confronto, è stata eseguita un’analisi 3D completa di mezza simmetria del componente tang profondo e i risultati sono mostrati in Fig. 9. Lo stress nominale attraverso la gamba superiore singola tang è identico in entrambi i casi-ricordate che questa è la base di qualsiasi controllo di sanità mentale.

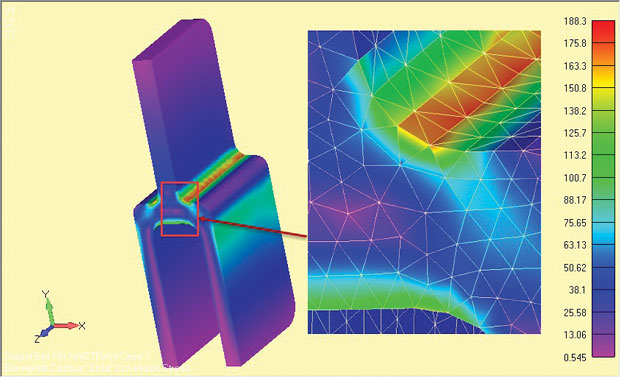Fig. 9: Modello 3D completo del tang profondo, che mostra i risultati di stress.

Le sollecitazioni locali della spalla sono inferiori di una piccola percentuale nel modello completo. Questo è per tre motivi. In primo luogo, la maglia relativamente grossolana del tet 3D è inferiore alla maglia locale molto fine del ceppo piano 2D. Non è stato effettuato un controllo di convergenza sul modello 3D.

In secondo luogo, c’è un piccolo cambiamento nella geometria delle superfici libere (+z, -z) rispetto alla sezione z = 0 a causa dei filetti finali. In questo caso, l’effetto è trascurabile poiché i filetti sono lontani dalle regioni della spalla. In molti componenti, tuttavia, ci saranno filetti locali e esauriranno i dettagli. che varierà la geometria da una semplice faccia planare xy. Le variazioni di stress locali alle facce terminali libere possono essere stimate o controllate con un modello 3D completo.

Infine, l’ipotesi di deformazione piana di un vincolo z fisso a sezioni +z,-z non è vera per un componente a profondità finita. Lo stress z si diffonderà a zero sulle facce libere “reali”. Questo effetto è mostrato in Fig. 10, che utilizza il modello 3D così com’è e anche come simulazione dello sforzo piano z.

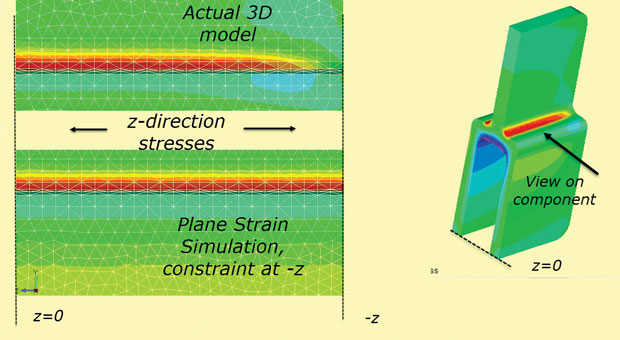Fig. 10: Diffusione dello z-stress verso la superficie libera.

Veloce ed efficiente

Le analisi delle sollecitazioni piane e delle deformazioni piane sono metodi 2D utili che spesso possono integrare modelli 3D su vasta scala. Non tutte le caratteristiche possono essere rappresentate, ma con un po ‘ di ingegno, gli stress in aree chiave possono almeno essere stimati. La motivazione per l’utilizzo dei metodi è quella di consentire un’analisi rapida ed efficiente con geometria 2D e costruzione di mesh semplici.