例を持つ貪欲なアルゴリズム：貪欲な方法とアプローチ

貪欲なアプローチを理解するには、再帰とコンテキスト切り替えの実用的な知識が必要です。 これは、コードをトレースする方法を理解するのに役立ちます。 あなたはあなた自身の必要かつ十分な声明の観点から貪欲なパラダイムを定義することができます。

二つの条件は貪欲なパラダイムを定義します。

• 各段階的な解は、最も受け入れられる解に向かって問題を構造化しなければなりません。
• 問題の構造化が有限数の貪欲なステップで停止できれば十分です。

理論化を続けて、貪欲な検索アプローチに関連する歴史を説明しましょう。

この貪欲なアルゴリズムのチュートリアルでは、次のことを学びます:

• 貪欲アルゴリズムの歴史
• 貪欲な戦略と意思決定
• 貪欲なアプローチの特徴
• なぜ貪欲なアプローチを使用するのですか？
• アクティビティ選択問題の解決方法
• 貪欲なアプローチのアーキテクチャ
• 貪欲なアルゴリズムの欠点

貪欲なアルゴリズムの歴史

:

• 貪欲アルゴリズムは1950年代に多くのグラフウォークアルゴリズムに対して概念化された。
• Esdger Djikstraは最小スパニングツリーを生成するアルゴリズムを概念化した。 彼はオランダの首都アムステルダム内のルートのスパンを短縮することを目的とした。
• 同じ十年に、PrimとKruskalは、計量されたルートに沿った経路コストを最小限に抑えることに基づいた最適化戦略を達成しました。
• 70年代、アメリカの研究者、Cormen、Rivest、Steinは、古典的なintroduction to algorithmsの本の中で貪欲な解の再帰的な部分構造化を提案しました。
• Greedy search paradigmは、2005年にNISTレコードに別のタイプの最適化戦略として登録されました。
• これまで、OPEN-shortest-path-first(OSPF)や他の多くのネットワークパケットスイッチングプロトコルなど、webを実行するプロトコルは、ネットワークに費やされる時間を最小化するために貪欲な戦略を使用していました。

貪欲な戦略と意思決定

その最も簡単な形の論理は、”貪欲”または”貪欲ではない”に煮詰められました。 これらの文は、各アルゴリズム段階で進めるために取られたアプローチによって定義されました。

例えば、Djikstraのアルゴリズムは、コスト関数を計算することによってインターネット上のホストを識別する段階的な貪欲な戦略を利用した。 Cost関数によって返された値は、次のパスが”greedy”か”non-greedy”かを決定しました。

要するに、アルゴリズムは、どの段階でも局所的に貪欲ではないステップを踏むと、貪欲でなくなります。 貪欲な問題は、貪欲のそれ以上の範囲で停止します。

貪欲法の特徴

貪欲法アルゴリズムの重要な特徴は次のとおりです:

• リソースの順序付きリストがあり、コストまたは値の属性があります。 これらは、システム上の制約を定量化します。
• 制約が適用される時間内にリソースの最大量を取ることになります。
• たとえば、アクティビティスケジューリング問題では、リソースコストは時間単位であり、アクティビティはシリアル順に実行する必要があります。

なぜ貪欲なアプローチを使用するのですか？

貪欲なアプローチを使用する理由は次のとおりです:

• 貪欲なアプローチにはいくつかのトレードオフがあり、最適化に適している可能性があります。
• 一つの顕著な理由は、すぐに最も実現可能な解決策を達成することです。 活動選択問題（後述）では、現在の活動を終了する前にさらに活動を行うことができれば、これらの活動を同じ時間内に実行することができます。
• もう一つの理由は、すべての解を組み合わせる必要なく、条件に基づいて問題を再帰的に分割することです。
• 活動選択問題では、”再帰分割”ステップは、項目のリストを一度だけスキャンし、特定の活動を考慮することによって達成される。

アクティビティ選択問題の解決方法

アクティビティスケジューリングの例では、すべてのアクティビティに”開始”と”終了”の時間があります。 各アクティビティは、参照のために番号で索引付けされます。 アクティビティには2つのカテゴリがあります。

1. 考慮された活動：活動であり、複数の残りの活動を行う能力が分析される参照である。
2. 残りの活動:考慮された活動よりも前の一つ以上の指標での活動。

合計期間は、アクティビティを実行するコストを与えます。 つまり、（finish-start）は、活動のコストとしての期間を与えます。

貪欲な範囲は、考慮された活動の時間に実行できる残りの活動の数であることがわかります。

貪欲なアプローチのアーキテクチャ

ステップ1)

考慮されるインデックスとしてインデックス0から始まる活動コストのリストをスキャンします。

ステップ2)

時間によってより多くの活動を終了できる場合、考慮された活動が終了したら、一つ以上の残りの活動の検索を開始します。

ステップ3)

残りのアクティビティがない場合、現在の残りのアクティビティが次の考慮されたアクティビティになります。 新しいアクティビティを考慮して、ステップ1とステップ2を繰り返します。 残りのアクティビティが残っていない場合は、手順4に進みます。

ステップ4)

考慮されたインデックスの和集合を返します。 これらは、スループットを最大化するために使用されるアクティビティ指標です。

コードの説明

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

コードの説明:

1. インクルードされたヘッダーファイル/クラス
2. ユーザーが提供するアクティビティの最大数。

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

コードの説明:

1. ストリーミング操作の名前空間。
2. 時間のタイムスタンプのクラス定義。
3. 時間のデフォルトコンストラクタ
4. 時間変数。

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

コードの説明:

1. activity
2. タイムスタンプからのクラス定義duration
3. タイムスタンプを定義するすべてのタイムスタンプは、既定のコンストラクターで0に初期化されます

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

コードの説明:

1. schedulerクラス定義のパート1。
2. 考慮インデックスは、配列をスキャンするための出発点です。
3. 初期化インデックスはランダムなタイムスタンプを割り当てるために使用されます。
4. アクティビティオブジェクトの配列は、new演算子を使用して動的に割り当てられます。
5. スケジュールされたポインタは、greedの現在のベース位置を定義します。

Scheduler(){ considered_index = 0; scheduled = NULL;......

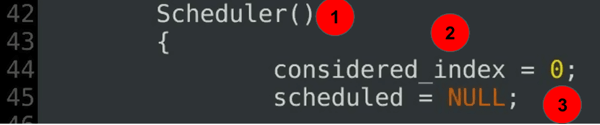
コードの説明:

1. schedulerコンストラクタ-schedulerクラス定義のパート2。
2. 考慮されるインデックスは、現在のスキャンの現在の開始を定義します。
3. 現在のgreedy範囲は、開始時には未定義です。

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

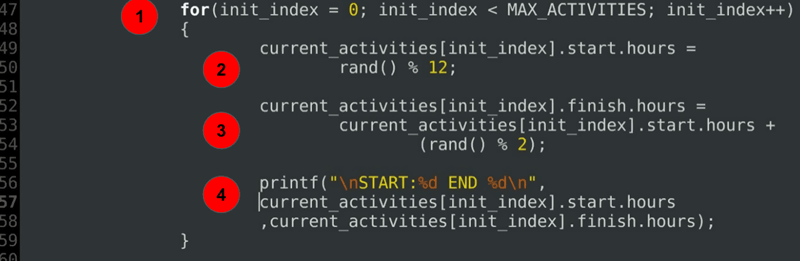
コードの説明:

1. 現在スケジュールされている各アクティビティの開始時間と終了時間を初期化するforループ。
2. 開始時刻の初期化。
3. 初期化の終了時刻は、常に開始時刻の後または正確に開始時刻になります。
4. 割り当てられた期間を出力するデバッグステートメント。

public: Activity * activity_select(int);};

コードの説明:

1. パート4-schedulerクラス定義の最後の部分。
2. アクティビティセレクト関数は、開始点インデックスをベースとして、貪欲なクエストを貪欲なサブ問題に分割します。

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. スコープ解決演算子(::)を使用して、関数定義が提供されます。
2. 考慮されるインデックスは、値によって呼び出されるインデックスです。 Greedy_extentは、考慮されたインデックスの後に初期化されたインデックスです。

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

コードの説明:

1. コアロジック-貪欲な範囲は、活動の数に制限されています。
2. 現在の活動の開始時間は、考慮された活動(考慮されたインデックスによって与えられる)が終了する前にスケジュール可能としてチェックされます。
3. これが可能な限り、オプションのdebugステートメントが出力されます。
4. アクティビティ配列の次のインデックスに進みます

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

コードの説明:

1. すべてのアクティビティがカバーされているかどうかを条件付きで確認します。
2. そうでない場合は、考慮されたインデックスを現在のポイントとして貪欲を再開することができます。 これは、問題文を貪欲に分割する再帰的なステップです。
3. はいの場合、greedを拡張するスコープなしで呼び出し元に戻ります。

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

コードの説明:

1. スケジューラを呼び出すために使用されるmain関数。
2. 新しいスケジューラがインスタンス化されます。
3. 貪欲なクエストが終わった後、activity型のポインタを返すactivity select関数が呼び出し元に戻ります。

:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

貪欲アルゴリズムの欠点

ソートのようなすべての部分問題に対して解が必要な貪欲な問題には適していません。

このような貪欲なアルゴリズムの練習問題では、貪欲な方法は間違っている可能性があります。

したがって、欲張りアルゴリズムの欠点は、現在の欲張り状態の先にあるものを知らないことを使用することです。

以下は欲張りな方法の欠点を描いたものです:

ここでツリーとして示されている貪欲スキャン（より高い値の高い貪欲）では、値：40のアルゴリズム状態は、次の値として29を取る可能性があります。 さらに、そのクエストは12で終了します。 これは41の値になります。

しかし、アルゴリズムが最適ではない経路を取ったか、征服戦略を採用した場合。 その後、25の後に40が続き、全体的なコスト改善は65になり、これは最適ではない決定として24ポイント高く評価されます。

貪欲なアルゴリズムの例

ほとんどのネットワークアルゴリズムは貪欲なアプローチを使用します。 以下は、いくつかの貪欲なアルゴリズムの例のリストです:

• プリムの最小スパニングツリーアルゴリズム
• 移動セールスマン問題
• グラフ-マップ着色
• Kruskalの最小スパニングツリーアルゴリズム
• Dijkstraの最小スパニングツリーアルゴリズム
• グラフ-頂点カバー
• ナップザック問題
• ジョブスケジューリング問題

要約：

要約すると、記事は貪欲なパラダイムを定義し、貪欲な最適化と再帰が、ある時点までの最良の解を得るのにどのように役立つかを示しました。 Greedyアルゴリズムは、Python、C、C＃、PHP、JavaなどのGreedyアルゴリズムとして、多くの言語で問題解決のためのアプリケーションに広く取り入れられています。 貪欲アルゴリズム例の活動選択は，貪欲アプローチを用いて最大スループットを達成できる戦略的問題として述べた。 最後に，貪欲なアプローチの使い方のデメリットを説明した。