土壌レポートで最も広く使用されている値は土壌支持力です。 明白な理由は、ほとんどのテキストブックで与えられた基本的な例は、ほとんどの場合、足場の計画寸法を計算するために支持力を使用することで 簡易性および使い易さのために、この方法はまだ基礎設計のための基本的な土変数である。 しかし、その単純さは、足場が剛体として動作することを前提としています。 その特定の仮定は小さく、単一のコラムの土台のために実際にはよく働く。 しかし、大規模で多柱の基礎の場合、ほとんどのエンジニアは柔軟な分析を好みます。 柔軟な解析を手動で計算することは困難であり、ほとんどすべての場合、STAAD、SAFE、GT STRUDLなどのソフトウェアプログラムが困難になる可能性があります。 が使用される。 しかし、これらのコンピュータプログラムは、しばしば”路盤反応の係数”と呼ばれる入力を要求する。 多くのエンジニアはこの用語に精通しておらず、しばしばそれを支持力と比較しようとします。 ますます多くのエンジニアがソフトウェアを使用して基礎を設計するようになるにつれて、エンジニアはこの土壌パラメータの基本的な理解を持 支持力と路盤反応の弾性率との間に関係はありますか？
地盤反応係数(Ks)
この項は、変位の単位当たりの荷重強度として測定され、表されます。 英語の単位系では、kip/in2/inで表されることが多く、SIシステムではkN/m2/mで表されます。kip/in3（またはkN/m3）でこの用語を表現する人もいますが、誤解を招く可能性があります。 数値的には、kip/in3は正しいですが、測定値の物理的意義を適切に表しておらず、密度単位または体積測定と誤解される可能性があります。
数学的には、地盤反応係数は次のように表されます。
Ks=p/s(Eqn1)
ここで、p=接触圧力強度、s=土壌沈下
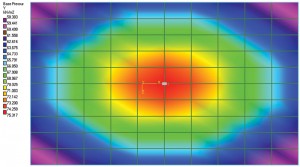
図1a:たわみ図と土壌圧力輪郭。
図1b:土圧の輪郭。
Terzaghiが述べたように、柔軟な基礎の接触圧力の適切な推定は非常に面倒なので、Ksは足場全体で一定のままであると仮定されます。 すなわち、足場のすべての位置の圧力と解決間の比率は一定している残る。 従って中心の負荷が付いている足場の変位の図表はdishing効果をもたらします。 足場の中心にあるポイントは、最も高い変位を経験します。 変位は中心から離れるにつれて減少します。 図1aは、単純なスラブ-オン-グレードの基礎を示しています。 それはSTAADの基礎で適用範囲が広い基礎である”マット”としてモデル化され、分析された;土は路盤の反作用の係数を使用して定義された。 この演習では、路盤反応係数のソフトウェアのデフォルト値を使用しました。 ディスプレイスメントダイアグラムは、前述のディッシング効果を示しています。 図1bは土圧の輪郭を示しています。 また、中心の圧力強度が最大であり、要素（またはノード座標）が中心から離れるにつれて減少することも明らかである。 したがって、圧力強度と沈降の比は一定であると仮定することができる。
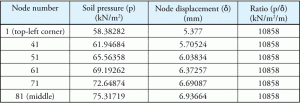
表1：土圧、節変位およびそれらの比。
同じ例の数字のいくつかを考えてみましょう。 土圧、対応する変位および比率は表1にリストされている。 点は、点が中心から長方形の足場の隅の最も遠い点に移動するときの圧力と変位の変化を示すために、対角線上に表されます。 図2は、マットスラブ上のポイントを示しています。
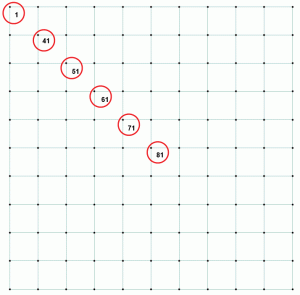
図2: 基準圧力、たわみおよび比を比較するために選択されたポイント。
これは、定義上、地盤反応係数（Ks）は足場全体の定数であり、プログラムはKsを土壌特性として使用しているため、驚くことではありません。 また、ソフトウェアのデフォルトKs値(10858kN/m2/m)は、表1で計算された定数比とまったく同じであったことに注意することも重要です。＜６ ３ ２ ２＞＜９ ９ ３ ４＞支持体反応からベース圧力を算出した。 支持反応と対応する変位の比も一定であると考えるかもしれない。 表2に示すように、比率はすべての値に対して一定ではありません。 Ks値はプログラム内でどのように使用され、ベース圧力はどのように計算されますか？
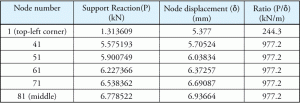
表2:反応および変位をサポートします。
支流面積
多くの場合、プレートの面積がノードに起因するか、言い換えれば、プレートの表面積に対する各ノードの影響を計算する仮定が行われます。 それはプレートの形状に依存します。 完全な正方形または長方形のプレートの場合、各ノードはプレート表面積のσに正確に影響します（図3a）。 しかし、一般化された四辺形の場合、ベストプラクティスは、プレートの質量の中心を計算し、その中心点から各辺の中間点まで線を引くことです。 図3bでは、網掛けされた領域は、対応するノードの影響表面積を表しています。
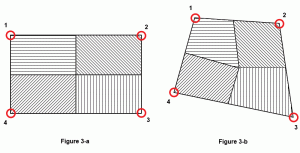
図3:ノード支流面積。
ばね支持定数
上記の支流面積計算は、線形ばね定数を計算するために市販のソフトウェアによって内部的に使用される重要な手順です。 プログラムは最初に足場の各ノードの支流面積を計算し、次に各ノードの対応する支流面積によって路盤反応の係数を乗算して、各ノードで線形ばね定数を
Kyi=Ks x Tai(Eqn2)
ここで、
Kyiはi番目のノードのばね定数
Taiはi番目のノードの影響面積
Ksは路盤反応係数
具体的な基礎分析のために、それらのばね-コンクリートとしてのみ、任意の引張力を運ばないと仮定されています。 支持反応を対応するノード支流面積で割ることにより，各支持ノードにおけるベース圧力を計算した。 上記の例を見ると、ノード1は残りのノードよりもはるかに小さい支流領域を持っています。 他のすべてのノードは同じ支流面積を有することにも留意することができる。 これは、ノード1の比率が他のノードと異なることを示す表2を説明しています。 図4は、異なるノードの支流領域を示しています。 ノード1は、ノード81の25％である支流の面積を有しています。 表3は、表1と表2の拡張であり、すべてのノードで一定の比率がどのように達成されるかを示しています。
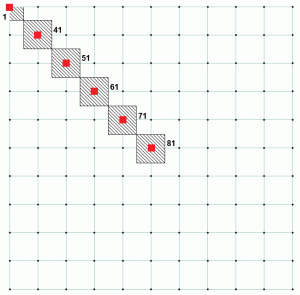
図4:選択したノードの支流面積。
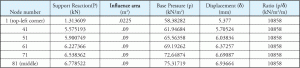
表3:反応、ベース圧力、変位、Ks定数。
許容沈下
支持力とは、土が安全に耐えることができる土圧の測定値です。 言い換えれば、支持力は、土壌がそれが失敗する前に耐えることができる圧力である。 二つの最も重要な土壌破壊基準は次のとおりです:
- せん断破壊
- 最大許容沈下
多くの要因の中で、基礎幅（B）が破壊基準に影響を与える可能性があります。 通常、せん断の失敗はより小さい基礎のために支配し、解決の失敗はより大きい基礎を支配する。 表4は、さまざまな基礎サイズと故障基準の関係を示す典型的な例です。
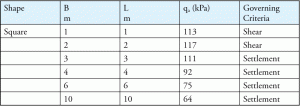
表4:許容沈下に対する最終許容支持力=25mmおよび所定の埋め込み深さ。
決済失敗を推定するために、許容決済値を仮定します（通常は25mmまたは1インチ）。 土壌が許容値以上に落ち着くと、土壌は失敗します。 従って、支持力の計算のために、正当な土の解決は使用され、構造エンジニアは足場を設計している間その価値に気づくべきである。 許容される土壌沈下値は、通常、土壌レポートの不可欠な部分です。
路盤反応係数を使用する理由
柔軟なマット基礎を設計するには、土壌の支持力の代わりに路盤反応係数を使用することが以前に述べられていました。 しかし、なぜ？ 答えは、財団がどのように行動するかの根底にある仮定にあります。
基礎は剛性または柔軟性があります。 支持力は、剛性の基礎を設計するために使用されるが、路盤反応は、柔軟な基礎のために使用されます。 剛体基礎の非常に仮定は、「剛体基礎は安定するときに平面のままであるため、基礎の基部上の路盤反応pの分布は平面でなければならない」というこ”図5aに示すように、その中心にロードされた単純に支持されたビームを考えてみましょう。staticsによって、R1=P/2とR2=P/2を得ることができます。 同じビームが偏心的にロードされている場合、反応は図5bに示すように計算することができます.
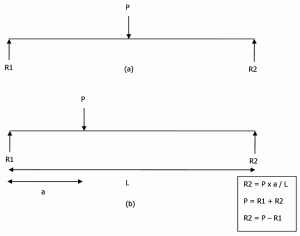
図5: 単純に支持されたビームのための反応。
同じ概念は堅い基礎設計のために拡張される。 しかし、最後のサポートの代わりに、基礎全体がサポートされています。 また，コンクリートスラブの相対剛性は土壌剛性よりもはるかに高いと仮定した。 従って、平板は負荷の適用の後でさえも平面に残ると仮定される。
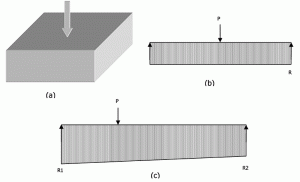
図6:分離された足場のサブグレード反応。
図6aは、中央にロードされた足場を示しています。 剛体の広いビームの類推から、P=R x L。 同様に、偏心的にロードされた足場の場合、反応は図6cに示すように、一方の端から他方の端まで直線的に変化します。式3と4は、端の反応を見つけるために解くことができます。 しかし、式のいずれも路盤反応の係数（Ks）を含んでいません。 したがって、「剛体足場のベース上の路盤反応の分布は、路盤の圧縮性の程度とは無関係である」それが休んでいる。 多くの著者が結論しているように、ほとんどの場合、この方法はより保守的な結果をもたらすので、剛性の基礎は支持力を使用して安全に設計するこ
P=1/2L(R1+R2)(Eqn3)
P x a=1/6B2R1+1/3B2R2(Eqn4)
しかし、マットファンデーションは、サイズが大きく、穴やグレードビームなどの負荷適用ポイントやその他の複雑さがある可能性があるため、柔軟なファンデーションとして設計されることが多い。 FEAソフトウェアの広範な可用性は、この傾向に貢献しています。 しかし、堅い基礎とは違って、適用範囲が広い基礎は線形路盤の反作用を持つことができない。 むしろ、それは基礎の圧縮性および構造剛性率に依存する。 適用範囲が広い基礎は2つの平板ポイント間の内部曲がることそして相対的な変位に服従します。 構造剛性が大きいほど、相対変位は小さくなります。 スラブ要素の非常に高い剛性を用いて試験し，荷重を加えた後にほぼ平面面を得た。 同様に、路盤反応の弾性率が大きいほど、圧力分布は小さくなる。 言い換えると、Ks値が高いほど、負荷印加点でより多くの圧力を吸収します。 それ故に、土の解決および外圧の機能である路盤の反作用の係数は適用範囲が広い基礎設計のために使用されます。
相関
支持力と路盤反応係数との相関の問題に対する最も一般的でおそらく最も安全な答えは、相関がないということです。 しかし、両方とも土壌容量の測定値であり、これら2つのパラメータのいずれかを使用して通常の基礎を設計することができるため、1つが必要です。
ここでも、Ksの定義は単位決済あたりの圧力です。 言い換えれば、土壌容量は、所定の変位のための圧力に耐えることができます。 以前の議論から、支持力でさえ許容される和解があることも明らかである。 従って路盤の反作用の係数が単位の解決ごとの軸受け容量であることを結論することは誘惑している。
この結論は、ボウルズが提示した方程式と非常によく似ています。
SI:Ks=40(SF)qa kN/m3(Eqn5)
FPS:Ks=12(SF)qa k/ft3(Eqn6)
ここで、SF=安全係数、qaは許容支持力です。
式5および式6では、まず許容支持力に安全係数を乗じて最終支持力に変換します。 著者は1インチまたは25mmの決済を想定していました。 最終的な方程式は、最終的な支持力を仮定された沈下で割ることによって定式化される。
方程式のより一般的な形式は次のように書くことができます:
Ks=
応力/変位(Eqn7)
ここで、
i=安全係数
qaは許容支持力
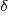は許容土壌沈下
これらの式は、適切な安全係数を使用しなければならないことを明確に示しており、Ks値は許容支持力ではなく究極の支持力と比較して良好であ 安全率はプロジェクトおよび地質工学エンジニアによって変わることができる。 他の重要な要因は計算された軸受け容量のための仮定された正当な解決である。
同様に、FEA分析によって報告されたベース圧力値は、支持力と直接比較することはできないことに留意すべきである。 最高の基礎圧力は安全率によって倍増され、次に土の正当な軸受け容量と比較されるべきです。
しかし、上記の式には制限があります。 それらは解決の失敗が支配する足場に適用することができるがせん断の失敗が正当な解決の限界に達する前に起こる足場と関連していることが したがって、エンジニアはこれらの方程式を使用する前に注意する必要があります。
結論
支持力と路盤反応係数との相関は、せいぜい推定値である。 それは推定に使用することができる版の負荷テストによって定められるKsの価値は利用できれば常に使用されるか、または可能な限り要求される しかし、上記の議論は、これらの値への洞察を与え、エンジニアが路盤反応の弾性率の物理的意義を理解するのに役立ちます。 そして、いつものように、構造エンジニアは土の剛さおよび軸受け価値を終了する前に地質工学エンジニアの専門家に相談するべきである。▪