はじめに
競合リスク(CR)は、18世紀以来、イベントまでの時間分析の特別なケースとして認識されてきました。 統計的または数学的な分野での仕事は、DavidとMoeschbergerのモノグラフを含む新しい開発を取り入れて出版されていることがあります。1さまざまなタイプのアウトカムに関するデータがより広範で明確で正確になるにつれて、CRは、病気のより良い理解に必要な、イベントまでの時間分析の中で重要なタイプの分析として再浮上しました。 数学的結果と応用分野との間の接続を行う必要がありました。 いくつかの著者は、CRの状況の理解に貢献してきました。2、3他の著者は、技術を強化し、開発し、いくつかのケースでは、適用された統計のための利用可能なすぐに使用できるコンピュータコードを作4,5,6
イベント時間分析の概要
多くの研究では、結果は縦方向に観察されます。 このようにして、コホート内のすべての被験者は、イベントが発生するまで一定期間観察されます。 例えば、関心のある事象は、死亡、心臓発作、または癌の再発であり得る。 研究の目的は、イベント発生の確率、または治療または被験者特性のような関心のある共変量との関連を推定することであり得る。 使用される統計分析は、イベントまでの時間分析または時には生存分析と呼ばれています。 事象の確率を推定する最も一般的な方法は、慣習的にKaplan-Meier7(KM)または積限界法と呼ばれるノンパラメトリック法です。 生存のためのKM推定の主な仮定は、打ち切り観測が十分に長く続く場合にイベントを経験するということです。
この論文の残りの部分については、イベントの確率ではなく、イベントの確率が与えられます。 例えば、生存の確率の代わりに、死亡の確率が提示され、これは、KM推定器の補数を使用して推定することができる:1−KM。
競合リスクの概要
研究の参加者が複数のタイプのイベントを経験することは珍しいことではありません。 CRの状況は、あるタイプのイベントの発生が関心のあるイベントを観察する能力を変化させたときに発生します。 宮坂他8は、米国ミネソタ州オルムステッド郡で1986年から2000年の間に心房細動と診断された患者のコミュニティベースのコホートに関する研究を実施した。 主な転帰は認知症の発症であった。 フォローアップの中央値は4.6年でした。 他のタイプの出来事は脳卒中と死であった。 心房細動を有する2837人のうち、299人が認知症を有し、1638人が分析の時点で死亡した。 ストロークのある数値は報告されず、分析で打ち切りされます。 研究の結論は、心房細動を有する個人の間で認知症の発生率が一般的であることであった(KM法を用いた10.5年で5%)。 認知症前の脳卒中の発生は認知症の観察に影響を与えないため、CRイベントではありません。 議論のために、私たちは複数の脳卒中が認知症を引き起こす可能性があるという事実を無視します。 一方、事前認知症のない死は、認知症の観察を不可能にする。 したがって、認知症のない死は、認知症のエンドポイントのCRイベントです。 また、患者の行動の変化が認知症の診断を不可能にする可能性があるため、重度の頭部外傷はCRイベントとみなされる可能性があります。
Whalleyらの研究では、より微妙なCRの状況が発生している。心エコー検査の重要性の9。 228高齢の症候性患者のこのコホートは、心エコー検査を受け、心血管入院または心血管死亡のいずれかのために続いた。 この仮説は、心エコー検査の特徴が心血管イベントを予測するというものであった。 主な結果は、心血管死亡および/または入院を含む複合尺度として定義された。 このタイプの転帰では、心血管疾患以外の原因による死亡はCR事象であり、そのため、患者はもはや関心のある事象のいずれかを有する危険性がない。
全死因死亡率に対するバルサルタンvsバルサルタン+カプトプリルvsカプトプリル単独(VALIANT)10の効果を試験するために、931のセンターと24カ国にまたがる3腕、二重盲検、無作為化試験が実施された。 合計で、14 703左心室機能不全および/または心不全を有する心筋梗塞後の患者は、1:1:1の3つの腕に発生した。 任意の死は、イベントと考えられていたので、結果のこのタイプは、CRを持っていません。 この研究は、3つの腕の生存が異なっていたという仮説を支持した。 しかし、胃腸(GI)出血は、すべての3つの腕で重篤な副作用として同定された。 Moukarbel et al.11は、GI出血を予測することができる可能性のある要因を研究しました。 このエンドポイントでは、GI出血のない死亡は明らかなCRである。
CRの存在と適切な技術を適用する必要性を認識する研究者が増えています。 非STセグメント上昇急性冠症候群を有する972人の患者のコホート2001年と2005年の間にNñezらによって研究された。この研究の目標の1つは、急性心不全の再入院に関連する要因を見つけることでした。 研究された要因の中には、糖尿病、虚血性心疾患の既往歴、慢性腎不全、喫煙歴、および治療歴があった。 著者らは,再入院前に死亡などのCRの可能性を認識し,CR状況を説明するために特定の技術を正しく適用した。
Melberg et al.13は、2種類の治療を受けた症候性冠動脈疾患を有する1234人の患者のコホートを研究した: 冠動脈バイパス移植(n=594)または経皮的冠動脈介入(n=640)。 フォローアップ中に観察された301人の死亡のうち、42.5%は心臓死亡であり、残りは非心臓死亡であった。 著者らは、全死因死亡率、心臓死亡率および非心臓死亡率の結果を提示している。 彼らは、全死因死亡率の割合は、CRを考慮して正しく推定された心臓および非心臓死亡率の割合の合計であることを指摘している。 著者らは、全体的な死亡率にそれらを結合するのではなく、関心のある各事象を分析することの重要性を強調している。 このトピックは、MellとJeongによってより一般的なレベルでも説明されています。14
上記の例から推測できるように、CRが存在するときの主な質問は、CRを無視してCRを含む観測を打ち切り、またはCRを説明するかどうかです。 CRが無視され、CR観測値が打ち切りされると、分析は”通常の”イベントまでの時間シナリオに短縮されます。 このタイプの分析とソフトウェアの利用可能性に精通しているため、多くの研究者は以前の例に見られるように、このアプローチに頼っています。 しかし、統計学者の間だけでなく、この場合の事象の確率の推定が真の確率を過大評価することは全会一致で合意されている2,15,16,17,18。 次の自然な問題は、モデリングがこれらの境界内で実行できるかどうかです(CRを無視/打ち切り)。 これはより曖昧で、把握するのがより困難です。 そのような分析は価値がないわけではないかもしれませんが、その解釈はほとんど常に困難を伴います。 主な要件は、CRイベント(観測値が打ち切りされ、真の打ち切り観測値と混合された)が、関心のあるイベントとは独立している必要があることです。 この場合、CRイベントが存在しなかった場合の結果は共変量の効果として解釈できます。 しかし、この仮定は通常行うことができず、検証またはテストすることはできません。 結論として,CR観測値が打ち切りされるたびに,事象の確率の推定は誤りであり,共変量の効果の解釈は,関心のある事象とC r事象との間の独立性の知識がないため明確ではない。
分析がCRを考慮して実行された場合(および関心のあるイベントまたは打ち切りからはっきりとコード化された場合)、確率は正しく推定され、モデ 解釈を妨げる独立性の仮定はありません。 このように推定された共変量の係数は、観測された確率に対するその共変量の効果を表します。
いくつかの著者19,20は、シミュレーションを使用してテストのパワーの観点から二つのアプローチを比較しようとしました。 しかし、研究者は、主な問題は結果の解釈にあることを認識する必要があります。 テストがどれほど強力であるかにかかわらず、分析は研究の質問に答える必要があります。
イベントの確率の推定
イベントの確率を推定するためにKM法を適用するのが一般的です。 KM推定の典型的な式は次のとおりです
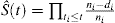
, ここで、t1t2t3niは、時間tiで危険にさらされている患者の数を表し、diは時間tiでのイベントの数です。
この式は代数的操作によって変換することができ、事象の確率を次のように表現することができる。:
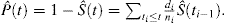
CRの存在下では、少なくとも2つのタイプのイベントがあります:添字eで識別される関心のイベントと、添字cで識別される競合リスクイベント。 KalbfleischとPrenticeは、CRの存在下で関心のあるイベントの確率の式を導入しました:
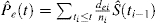
(1)と(2)の関係に注意するのは興味深いことです。 Diはtiにおける全てのイベントの数であるので、関心のあるイベントdeiの数と時間tiにおけるCRイベントdciの数との和として考えることができる。 したがって、任意のタイプのイベントの確率は、次のように分解することができます:
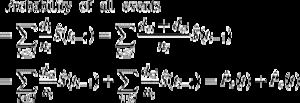
したがって、すべてのイベントの確率は、イベントの各タイプの確率で分解することができます。
1-KMを使用してCRの存在下で関心のあるイベントの確率を計算する場合、式(2)のすべてのイベントの生存率は、関心のあるイベントのみに基づくKM これは、後に示すように、結果に偏りがあります。 KM法の使用の主な前提は、検閲された患者が、十分に長く続くと、最終的にイベントを経験するということです。 しかし、KM法をCRの存在下で使用すると、関心のあるイベント以外のイベントを経験している患者は、もはや関心のあるイベントのリスクがないにも さらに、(3)に見られるnice分解は、1-KM式に対して実行することはできません。
適用された状況では、関心のない他のいくつかのタイプのイベントが存在する可能性があります。 この場合、すべてのCRイベントの傘の下にグループ化することができます。
CRの存在下でKM法を使用することは適切ではないことを例を通して示すことになる。
実施例の説明
ホジキンリンパ腫の治療の後期効果を研究するために収集されたデータセットを例示のために使用する。 主な結果は心臓病の入院です。 ホジキンリンパ腫は、主に若年成人に現れる癌の一種である。 その初期段階では、それはほぼ硬化性であり、10年の全生存率は70%である。 したがって、これらの患者のコホートは、治療の長期的な副作用を研究するのに理想的である。 ここで使用されるデータセットは、他の場所で報告されるより大きなコホートのサブセットです。 データはまた、当社の目的を果たすために変更されます。 例えば、簡単にするために、化学療法または放射線のいずれかを有する患者のみをデータに保持し、併用治療を有する患者を除いた。 CR(心臓入院なしの死亡)の割合を増加させるために、我々はすべての段階の患者を含めた。 いくつかのフォローアップと死亡日が帰属しました。 データに加えられた変更のために、この分析から臨床的結論を引き出すことはできない。 ここに提示されたデータは、689の心臓入院と93の死亡と467の記録を参照しています。
心臓入院率および心臓事象のない死亡率は、KM法(1)およびKalbfleischおよびPrentice21がこの目的のために導入した累積発生率関数(CIF)(2)の両方を用いて計算される。
競合するリスク状況に適用されたカプラン-マイヤー法は、イベントの真の割合を過大評価する
図1は、化学療法のみで治療されたグループの心臓入院のCIFと1-KMの推定値を示している。 1-KM推定値に対応する破線は、CIF推定値を表す実線の上にあります。 1-KMは常に事象の確率を過大評価することを数学的に示すことができる。 一般的な誤解は、2つのイベントが独立している場合、1-KMの推定値が正しいということです。 イベント間の独立性は最高でも常に疑問ですが、データが独立したイベントとしてシミュレートされている場合でも、CIF推定値と1KMの差が存在します。 差の大きさは、関心のあるイベントとCRイベントの両方のイベントの数に依存します。 宮坂らによる。、8KM法を用いた5年間の認知症の発生率は10.5%であった。 CR(死亡)の数は、イベントの総数の約四分の三であり、その推定値は観察されたものよりもはるかに大きい可能性があることを示唆している。
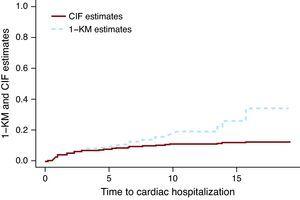
図1. 累積発生率関数vs1-Kaplan-Meier推定値。. CIF、累積発生率関数;KM、カプラン-マイヤー。
累積発生率関数は、任意の事象(心臓入院または死亡)の確率を構成確率
代数的にこれは(3)で証明されています。 しかし、それがどのように機能するかをより深く理解するために、すべてのイベントの確率から、一部が一方のイベントのCIFに参加し、他方のイベントのCIFに参加することがグラフィカルに示されます。 図2Aは、任意のイベントの確率を示しています:心臓入院または心臓入院なしの死亡。 図2Bには、10.7と10の間の曲線のみが含まれています。85年、ステップが表示されるように。 各ステップには円があります。 開いた円は死が観察されたステップに現れ、固体円は心臓入院が起こったステップにある。 パネルCの心臓入院のCIFには実円のステップが、図2Dの死亡曲線には実円のステップが含まれているため、各ステップが原因となる事象の確率に寄与します。 このようにして、任意の時点において、すべての事象の確率は、関心のある事象の確率とCRの確率との和である。 最後の3つのパネル(図2B-D)は、同じ時間ウィンドウを示し、ステップのサイズをそれらの間で比較できるように、y軸の長さが同じであることに注 表1は、1年、2年、3年、4年、および5年のこれらの確率を示しています。
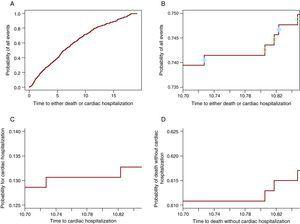
図2. すべてのイベントの確率を構成確率に分割します。 A.心臓入院または死亡の確率。 B.10.70-10.85年の時間の窓のための心臓入院または死亡の確率。 実線の円は心臓入院を示し、開いた円は心臓入院のない死亡を表しています。 C.時間の窓における心臓入院の確率10.70-10.85年。 D.時間の窓10.70-10.85における心臓入院のない死亡の確率。
表1. 任意のイベントの確率は、構成確率の合計です。
| 報告年 | 心臓入院確率 | 死亡確率 | 心臓入院または死亡のいずれかの確率 |
| 1 | 0.038 | 0.054 | 0.092 |
| 2 | 0.054 | 0.139 | 0.193 |
| 3 | 0.072 | 0.193 | 0.265 |
| 4 | 0.076 | 0.25 | 0.327 |
| 5 | 0.087 | 0.305 | 0.392 |
1-KMはイベントの確率を過大評価するため、心臓入院の1-KM推定値を死亡の1-KMに追加しようとすると、イベントの確率よりもはるかに高い率が得 いくつかのケースでは、得られた数は1よりもさらに大きく、これはCRの存在下では、1-KM推定値は確率さえないことを証明する。
累積発生率関数法は実際に事象の正しい確率を推定しますか?
この目的のために、500レコードのデータセットをシミュレートし、5年前に打ち切りがなく、タイプ1と2の2つのタイプのイベントがあるようにしました。 表2は、各タイプのイベントについて、その時点までに観測された数、粗レート、およびCIF推定値を示しています。 平等は、その時点までに検閲された観測がない場合にのみ発生します。 報告された年以内に検閲された観測値が存在する場合、平等は成立せず、確率を推定する正しい方法はcifであり、粗レートではありません。
表2. 5年までの検閲観測がない場合の2つのタイプのイベントの確率。
CIF、累積発生率関数。
結論として、CRの存在下での事象の確率を計算するには、KalbfleischとPrenticeによって導入された方法を使用する必要があります。
モデリング
分析における重要な側面は、共変量と関心のあるイベントとの間の関連性を、単独で、または他の因子を調整することです。 CRが存在しない場合、これはcox比例ハザード(Cox PH)モデルを使用することによって日常的に達成されます。22
CRの存在下では、Cox PHモデルには単純な解釈はありません。 2種類のイベントまでの時間が独立していると考えることができれば、結果はCRが存在しない状況での効果を示すものと解釈することができます。 しかし、独立性の仮定はめったに行われたりテストされたりすることができないため、Cox PHモデルからの結果は通常解釈できません。
Fine and Grayモデル
Fine and Gray6(F&G)は、CRの存在を可能にするためにCox PHモデルを変更しました。 技術的な修正は減少の重量と置かれる危険でCRの観察を保つことから成っている。 このようにして、F&G法は、サブディストリビューションの危険性をモデル化します。 F&Gモデルを使用して推定された効果は、サブディストリビューションハザード比の観点から、治療群間の現在の差と実際の差を示しています。 危険の比例性の仮定は依然として要件ですが、もちろんそれはサブディストリビューションの危険性を指します。 F&Gモデルは、ハザードの非比例性をモデル化するために時間依存係数を収容することができます。 このモデルは、関心のあるイベント(心臓入院)またはCR(死亡)の両方に適用することができます。
Cox PHおよびF&Gモデルをホジキンリンパ腫データセットに適用し、化学療法と放射線の治療オプションをテストしました。 この実施例(表3)では、Cox PHおよびF<6 6 0 6>gモデルからの結果は実質的に異なる(最初の2行)。 上述したように、CoxのPH結果は解釈可能ではなく、使用することができない。 第二の列は、放射線群の間でより多くの心臓入院があることを示し、第三の列は、化学療法群の間でより多くの死亡を示しています。 図3は、これらの結果をグラフィカルに示しています。 より進行した疾患を有する患者には化学療法単独で投与された可能性があり、これらの患者も癌で死亡する可能性が高かった。 一方,hodgkinリンパ腫診断後に長生きした早期の患者には放射線単独で投与されたと考えられた。 これらの患者に心臓病のような遅い副作用を開発するチャンスの多くがありました。
表3. Coxの比例した危険および良いおよび灰色モデルが用いられる場合の処置の効果。
CI、信頼区間、Cox PH、Cox比例ハザードモデル、F&G、ファインおよびグレーモデル、HR、ハザード比。
ハザード比は、化学療法群と比較して放射線群のハザードの増加を示している。
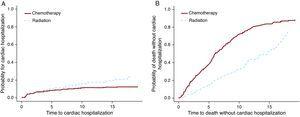
図3. 心臓入院および死亡に対する治療の効果。
この例からわかるように、結果の解釈は、統計学者と病気の完全な知識を持っている臨床医との間の協力の仕事です。
CRの存在は、データの分析と解釈の両方を複雑にします。 読者が結果を正しく解釈できるようにするには、一見重要ではないように見えても、観察されたイベントの詳細を含める必要があります。 したがって、エンドポイントが経時的に観察される場合、著者は、関心のあるイベント、CRの可能性があるかどうか、これらのタイプのイベントのいず CRの存在下では、関心のあるイベントの分析とCRの分析を含めることは有益であり、互いに補完し、結果を解釈するのに役立つ可能性があるためです。
ロジスティックアプローチ
まず、私たちがCRなしの枠組みの中にいると仮定しましょう。 結果が短い間隔(例えば、1年)内に発生すると予想される場合、多くの研究者にとって選択されるツールはロジスティック回帰である。 これは、コホート内のすべての個人が最小のフォローアップを持っている場合、この場合は1年に適しています。 実際、1年の死亡率の推定値は1KMの推定値と一致します。 一時的なカットオフポイントは、コホート内のすべての個人で同じである必要があります。 したがって、関心のある結果が1年死亡であり、コホート内の1人の個人が1年と2日で死亡した場合、その人は”1年での出来事はない”とみなされるべ”これは、カットオフポイントの後に多くの観測されたイベントが発生したときに理想的ではない分析に変換され、イベントの数を減らすことがで
CRが存在する場合、同じ基本ルールが適用されます。 コホート内のすべての個人は、時間のカットオフポイントとして選択された最小フォローアップを持っている必要があり、そのカットオフポイントは、コホート内のすべての人のために適用する必要があります。 係数とp値は一般に同じメッセージを与えますが、f&Gモデルと比較してロジスティック回帰ではまったく同じではありません。 まず、ロジスティック回帰では、係数はオッズ比の対数を表し、F&Gモデルではハザードサブディストリビューションの比の対数です。 さらに、ロジスティック分析では、すべてのイベントが使用されるわけではなく、もちろん別のモデルが使用されます。
電力計算
測定値がイベントまでの時間の場合、電力計算には2つの段階があります。 最初のステップは、特定の効果サイズを検出するために必要なイベントの数を計算することです。 次に、その事象の数を観察するのに必要な患者の数が計算される。 前のセクションでは、CRが存在する場合、CRの発生のために関心のあるすべてのイベントを観察することはできないことが強調されました。 イベントの数は電力の計算の中心であるため、CRが考慮されるように特別な注意を払う必要があります。 CRが考慮されていない場合、研究は力不足になり、したがって失敗する可能性があります(そしておそらく非倫理的です)。
ソフトウェア
CRAN(Comprehensive R Archive Network)サイト(http://cran.r-project.org/)上のオープンソースRソフトウェアは、Dr. ロバート*グレイは、CRのための完全な分析会計のために必要なツールを含みます。 したがって,関心のある事象に対する観測された確率プロットと,CR状況に対する修正logrank検定であるGray検定に基づくp値を得ることができた。 パッケージ内には、F&Gアプローチを使用したモデリング機能もあります。 Luca Scrucaは、要約型関数をパッケージに組み込むことにより、モデリング機能の出力配信を強化し、読みやすくしました。 このモデルは、ハザードの比例性をチェックする可能性があり、時間依存係数の項を含めることができます。 このコードは、左の切り捨てまたはクラスターデータには対応できません。 左の切り捨ては、患者ごとの複数/再発事象の分析または症例コホートの分析に有用であろう。 症例−コホート研究のためのコードが開発された(Pintilie e t a l.ら得ることができる。 周他24階層化されたデータに対応するためにF&Gモデルを拡張し、クラスタデータ用のバージョンも持つことになります。 この時点で、コードは両方のケースで著者から取得される可能性がありますが、CRANに提出される可能性があります。
STATA11は最近、F&Gモデルを実装しました。 STATAを使用して得られたグラフは、観測された確率グラフではなく予測グラフであることに注意する必要があります。 予測曲線を使用する場合には、2つの注意点があります: a)線は常にハザードの比例性が満たされているかのように表示され、b)各曲線のステップ数は各サブグループのイベントの数よりも大きくなり、実際よりも多くのイベントがあるという印象を与えます。
結論
いくつかのエンドポイントに対する完全なフォローアップを伴う大規模なデータセットの可用性は継続的に増加しています。 また、心不全による死亡や疾病管理、または局所疾患の管理など、正確なエンドポイントに関する分析の必要性が高まっています。 これらのエンドポイントはすべて潜在的にCRを持つ可能性があります。 したがって、CRは設計段階から結果の解釈まで考慮することが不可欠です。 独立性を考慮すると、Cox PHモデルは限られた値を持つかもしれませんが、KM推定値は正しくなく、解釈することはできません。 したがって、CIFおよびF&Gモデルのような特定の技術をRおよび部分的にSTATAで利用できるように適用する必要があります。
利益相反
いずれも宣言されていません。