전기장 전자는 항상 스칼라 전위 함수의 구배로 표현 될 수있다
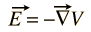
자기장에 대한 일반적인 스칼라 잠재력은 없지만 벡터 함수의 컬로 표현 될 수 있습니다
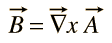
이 함수는”벡터 전위”라는 이름이 부여되지만 스칼라 전위가있는 방식으로 작업과 직접 관련이 없습니다.
벡터 전위는 암페어의 법칙과 일치하도록 정의되며 전류 나 또는 전류 밀도 제이(자기장의 소스). 다양한 텍스트에서,이 정의는 다음과 같은 형태를 취합니다
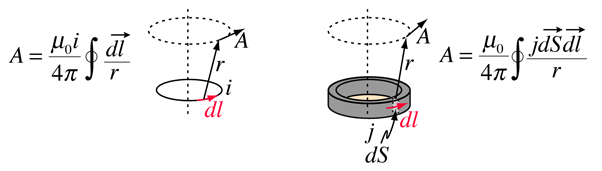
벡터 전위에 대한 한 가지 근거는 주어진 소스 전류 형상에서 직접 자기장을 계산하는 것보다 벡터 전위를 계산하는 것이 더 쉬울 수 있다는 것입니다. 그것의 일반적인 신청은 전자기파의 이론 그리고 묘사를 안테나에 입니다.
이후 자기장 B 으로 정의 컬의하고,벡터에 의해 신원의 컬 그라디언트는 동일하게 제로,다음 임의의 함수로 표현할 수 있으로 그라데이션의 스칼라 기능을 추가할 수 있습 값을 변경하지 않고의 B 에서 얻어진다. 즉,’자유롭게 대체 할 수있는 곳
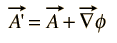
이러한 변환은 게이지 변환이라고하며 전자기 이론에서 특정 유형의 계산을 활용하는 데 사용 된 많은”게이지”가 있습니다.