Forenkle FEA Modeller: Plane Stress Og Plane Strain

Redaktørens Notat: Tony Abbey lærer levende NAFEMS FEA klasser I USA, Europa og Asia. Han underviser OGSÅ NAFEMS e-læring klasser globalt. Kontakt .for detaljer.

en Tidligere Desktop Engineering artikkel («Simplify FEA Simulation Models Using Planar Symmetry») forklarte at selv med kraftige moderne datamaskiner, er det ofte en motivasjon til å bruke forenklingsteknikker I structural finite element analysis (FEA). Denne oppfølgingen beskriver hvordan to nært beslektede metoder kan brukes til å ta 2D skiver gjennom en kompleks struktur på regioner av interesse. DE RESULTERENDE FEA-modellene kan gi verdifull innsikt i lokale påkjenninger raskere og mer effektivt enn en full 3d-modell. De vil ikke fortelle hele historien, men er verdifulle verktøy for CAE ingeniør.

DE TO FEA-metodene kalles planspenning og planbelastning. Begge bruker 2d plane elementer som ser ut som tynne skallelementer og er meshed ved hjelp av plan overflate geometri.

Plane Stress Analyse

Fig. 1 viser viktige fakta om flyet stress analyse. Den strukturelle regionen antas å ligge I 2d xy-planet, med den tredje strukturelle dimensjonen relativt liten. I figuren er dette tykkelsen i z-retningen. Påkjenninger finnes i 2d-flyet som sigma x, sigma y (direkte påkjenninger) og sigma xy (i-plan skjærspenning). Hver av disse spenningene er konstant gjennom tykkelsen som vist i innsatsen. I tillegg kan det ikke være stress i z-retningen. Dette forholdet mellom stress og belastning er definert I 2d-planspenningselementer som brukes i denne typen analyse.

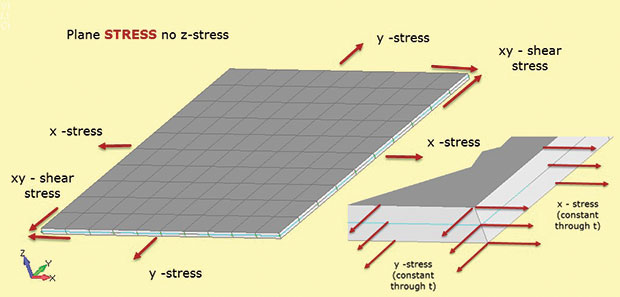Fig. 1: Plane stress; stress tilstand forutsetninger.

mangelen på z-stress er måten å huske elementtypebetegnelsen flyspenning (dvs. bare in-plan stress tillatt). Det er heller ingen gjennomtykkelsesskjærspenninger. Vi kunne laste flyet stress modell I Fig. 1 med en bi-aksial belastning og beregne sigma x og sigma y. det er ingen sigma z. Vi kan også beregne tilsvarende i-plan stammer e-x og e-y. hvis vi bruker en skjærbelastning, kan vi finne skjærspenning sigma xy og skjærbelastning e-xy. Interessant kan vi også beregne gjennom tykkelsesstammen e-z. Dette er ikke null, da modellen er fri til å tynne ned i z da den strekker seg i x og y. Det er ingen begrensning utenfor flyet for å forhindre dette. I noen løsere kan vi gjenopprette gjennom tykkelse belastning e-z og bruke den til å beregne endringen i tykkelse. (Hvis modellen er i bi-aksial komprimering, blir z-delen tykkere). Dette er vanligvis betraktet som en sekundær belastning og kan ikke være tilgjengelig for utgang-men det er der og kan beregnes manuelt om nødvendig.

Fig. 2 viser en aluminiumskabel komponent. Lug stikker ut fra et sammensatt ark layup som har plies plassert og limt over tangs (eller ben) og nedre delen av kroppen. Tangs overfører lasten som påføres på lug inn i komposittstrukturen. I praksis vil lagene bli trappet for å tillate en jevn skjæroverføring gjennom bindingen inn i kompositten. Skjæroverføringen i kompositten simuleres her ved diffust overflatetraksjonskrefter som «trekker» på tangene. Disse balanserer den påførte lasten.

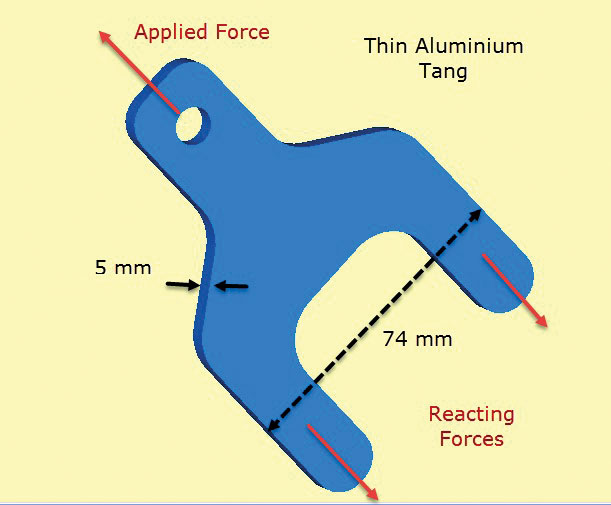Fig. 2: Tynnvegget aluminium tang overføre belastningen til kompositt struktur.

nøkkelforutsetningen her er at gjennom tykkelsesspenninger er null og in-planspenninger er konstant gjennom tykkelse i komponenten. Dette betyr at den lokale detaljene i skjærbelastningsoverføringen fra kompositt til tang er dårlig modellert. Men fokus for denne analysen er å kontrollere dimensjonering av lug og tang tverrsnitt klar av kompositt, ved hjelp av in-plane spenninger.

tykkelsen på komponenten er liten sammenlignet med andre dimensjoner. Denne verdien er inngang som den faktiske tykkelsen i planetspenningselementdefinisjonen.

Fig. 3 viser FEA-modellen og beregnede maksimale hovedspenninger. Områdene av interesse er rundt lug og skulderradier. I den virkelige verden vil stresstilstanden ved stresskonsentrasjonene være 3D, og gjennom tykkelse vil sigma z-spenninger og skjærspenninger balansere lokalt. Det er imidlertid veldig rimelig her å anta at spenningen i flyet dominerer. Dette er den samme antagelsen som er implisitt i de fleste tradisjonelle spenningskonsentrasjoner (Kt) beregninger som finnes i håndbøker.

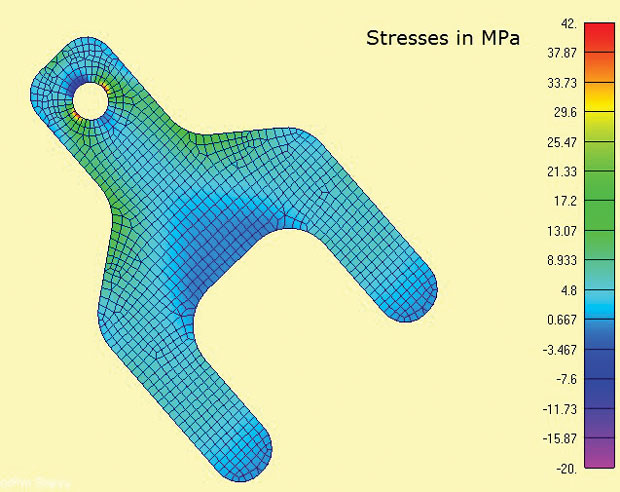Fig 3: 2d Plan stresselementer som viser maksimale hovedspenninger

En av de praktiske funksjonene i flyspenningsanalysen er at det er en strengt 2d-analyse, så bare tre frihetsgrader (DOF) må begrenses (in-plan oversettelser x, y og rotasjon om z-aksen). Dette gir seg til 3-2-1 minimum begrensningsmetoden med balansert belastning. I ET 2d-tilfelle degenererer dette til en 2-1-metode. En node har dof x og y begrenset, en annen passende ortogonal node har dof x begrenset. Dette gjør at reaksjonsbelastningen i tangene kan påføres direkte som diffust balansebelastning. Det ville være vanskelig å simulere denne grensetilstanden via begrensninger til bakken.

gjennomgående tykkelse e-z belastning og dermed tynning av tangs kan beregnes som en sekundær effekt.

Analyse Av Planbelastning

Fig. 4 viser essensen av flyet belastning metoden. IGJEN brukes 2D plane elementer, men med subtilt forskjellige forutsetninger. De in-plane spenninger x, y og xy er utviklet som før. Men denne gangen er det ut-av-planet, eller gjennom tykkelse z belastning som er satt til null. Så flytestamanalyse tillater bare stammer i flyet. Dette fungerer bra for å representere tykke strukturer som vist. Tilstedeværelsen av dette mye materiale har en tendens til å stabilisere komponenten og hindre at den strekker seg i z. Dette betyr også at konstant gjennomtykkelse z spenninger utvikles i strukturen. Dette spenningsbelastningsmaterialforholdet er definert I 2d-planbelastningselementer som brukes i denne typen analyse.

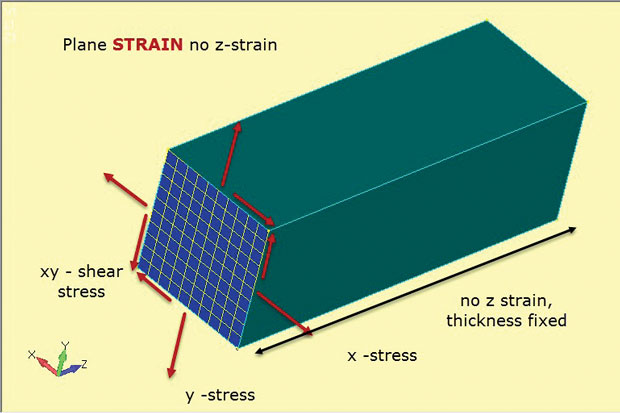Fig. 4: Plan strain analyse; stress og belastning tilstand forutsetninger.

figuren viser retningen TIL 2d-planbelastningselementene som en kuttdel gjennom en typisk dyp komponent. Forutsetningen er at stresstilstanden ved denne kuttdelen vil bli duplisert på et hvilket som helst xy – planskåret (z-stasjon) gjennom komponenten. Komponenten antas å være prismatisk (har et konstant tverrsnitt) ned i lengden.

i praksis bruker vi denne metoden der stresstilstanden varierer sakte fra fly til fly i en dyp komponent. Det bør være nok materiale gjennom dybden for å stabilisere og eliminere gjennom tykkelsen belastning. Dette er det samme prinsippet som brukes på bruddseighetsprøver vist I Fig. 5. En svikt under planbelastningsforhold er vist for den midtre delen av den tykke prøven. Feilen ved frie kanter og den tynne delen er en annen modus, mer som en planstressstilstand. En plan strain FEA modell ville per definisjon være en god representasjon av midtlinjen tykke prøven atferd, men ikke av de frie kanter eller tynne prøven.

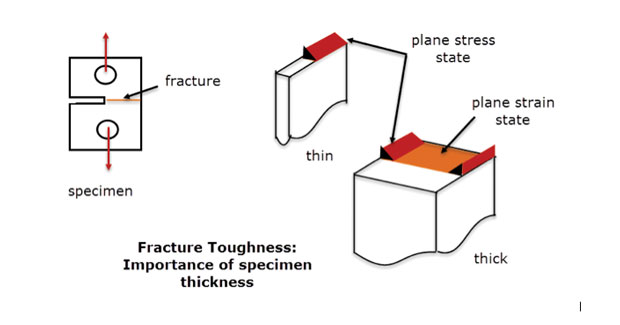Fig. 5: bruddseighetsprøver; tynne og tykke seksjoner.

Fig. 6 viser en annen komponent som brukes i en sammensatt struktur, som danner en bundet ledd. Her er seksjonen konstant og dyp nok slik at vi kan anta at stressene også er konstant med dybde. De frie endeflatene (ved + z, – z) vil ha en annen lokal spenningstilstand (faktisk planspenning, som nevnt), men målet med denne analysen er å sjekke nettavsnittspenningen på midtlinjen (z = 0).

2d plan strain analysenettet er vist delt inn I 3d-komponenten I Fig. 7. Snittskåret er definert ved stasjon z = 0.

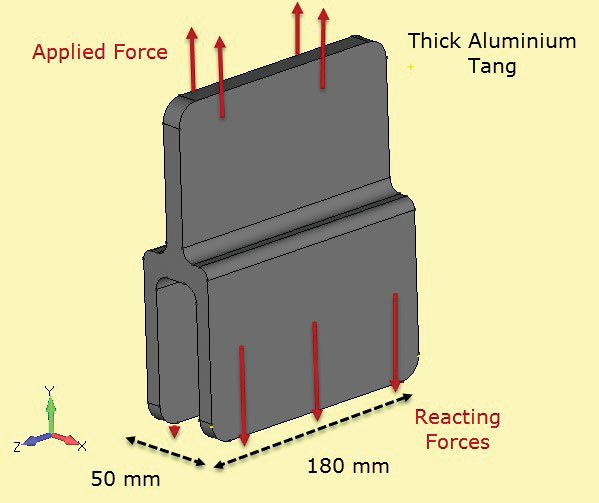Fig 6: dyp-seksjon aluminium tang.

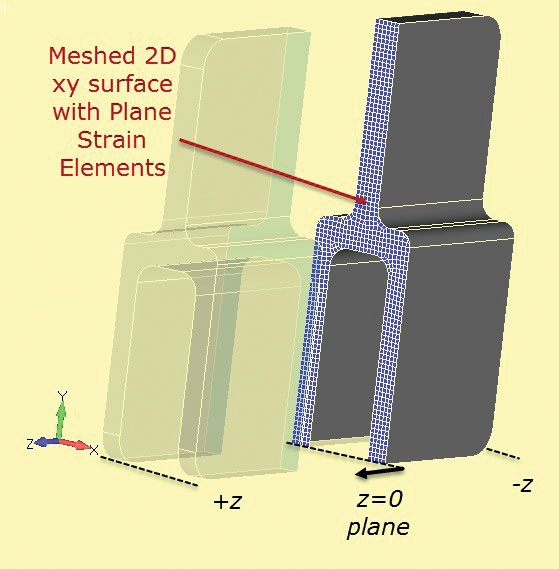Fig. 7: Seksjon skjær gjennom solid seksjon for å utvikle 2D plan strain seksjon.

en veldig fin 2d plan strain mesh kan brukes, som vil kjøre svært raskt i forhold til en full 3d-modell. 2-1 begrensningsmetoden brukes som før. Lastingen må vurderes nøye. «Tykkelsen» av planstammen er ganske vilkårlig, og er vanligvis satt til 1,0 som standard. Hvis lasten på komponenten beregnes som en løpende last gjennom dybde (N/m, Lbf/tomme etc.) da denne verdien kan brukes direkte på flyet belastning mesh. Det er nyttig å velge en seksjon, for eksempel enkelt tang og anslå nominell eller gjennomsnittlig stress i denne delen for hele komponenten. Dette kan brukes som en sunnhet sjekk i flyet belastning analyse. Feil lasting er trolig hovedårsaken til feil i denne metoden.

resultatene av analysen er vist I Fig. 8 og vis tydelig områdene med høyt stress rundt skulderfileten. Spenningene er gyldige for komponentens sentrale dybderegion (z = 0).

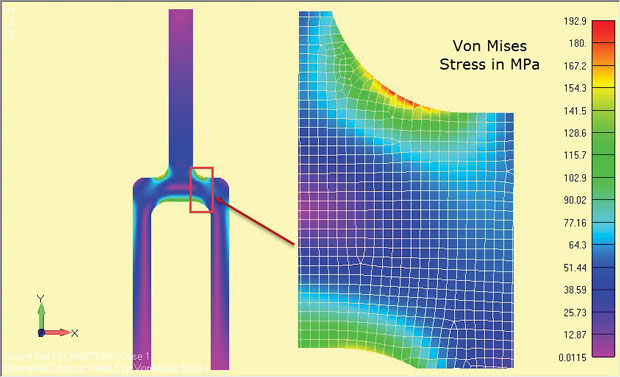Fig. 8: Plane stamme analyse resultater av en dyp tang komponent.

spenningsmengdene som brukes, vil avhenge av løsningen som brukes. Noen løsere ignorerer z-retningsspenninger som sekundære og gjenoppretter spenningen i flyet. De viktigste påkjenninger og von Mises påkjenninger deretter forholde seg TIL EN 2d in-plane stress tilstand. Hvis z-retningsspenningen gjenvinnes, bør den tydelig identifiseres, slik AT 2d-stresstilstanden i xy-flyet kan identifiseres.

hva representerer z-retningsspenningen? Det er stress utviklet på grunn av håndheving av null z retning belastning. Spenningen virker som om de frie endeflatene til den prismatiske delen ble løst. På det sentrale planet av en dyp seksjon komponent disse vil være komplementære påkjenninger som trengs for å holde null z retning belastning tilstand. I virkeligheten når vi beveger oss mot de frie overflateflatene, faller z-spenningen til null og blir en planspenningsfordeling (som sett i den tykke bruddmekanikkprøven).

i mange tilfeller, for eksempel en trykksylinder, er endeflatene avkortet og vil faktisk utvikle et aksialt stress på grunn av aksiale krefter. Dette vil være et annet stress fra det induserte aksiale stresset i planstammeanalysen. En håndberegning vil være nødvendig for å beregne aksialspenninger, eller mulig en supplerende aksisymmetrisk modell for trykkbeholdere.

den enkle geometri og mesh konstruksjon egner seg godt til» hva-hvis » studier eller mer formelle form optimalisering studier.

til sammenligning ble en halv symmetri full 3d-analyse av den dype tangkomponenten gjort og resultatene er vist I Fig. 9. Den nominelle spenningen over det øvre enkelt tangbenet er identisk i begge tilfeller-husk at dette er grunnlaget for enhver sunnhetskontroll.

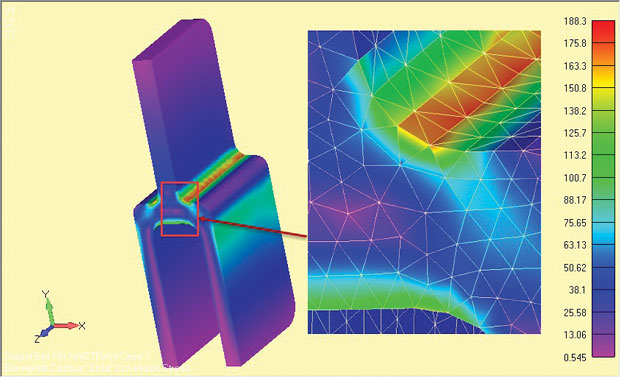Fig. 9: Full 3d-modell av deep tang, viser stress resultater.

de lokale skulderbelastningene er lavere med en liten prosentandel i hele modellen. Dette er av tre grunner. For det første er det relativt grove 3d-tet-nettverket dårligere enn det meget fine 2d-planstammen lokalt nett. En konvergenskontroll PÅ 3D-modellen er ikke utført.

For Det Andre er det en liten endring i geometri på de frie overflatene (+z, -z) sammenlignet med z = 0-delen på grunn av endefiletene. I dette tilfellet er effekten ubetydelig da filetene er borte fra skulderområdene. I mange komponenter vil det imidlertid være lokale fileter, og gå tom for detaljer. som vil variere geometrien fra et enkelt xy plan ansikt. Lokale stressvariasjoner ved frie endeflater må kanskje estimeres eller kontrolleres med en full 3d-modell.

endelig er planbelastningsforutsetningen for en fast z-begrensning ved +z, – z-seksjoner ikke sant for en endelig dybdekomponent. Z-stresset vil diffundere til null ved de «ekte» frie ansikter. Denne effekten er vist I Fig. 10, som bruker 3d-modellen som den er, og også som en simulering av flyet belastning z stress.

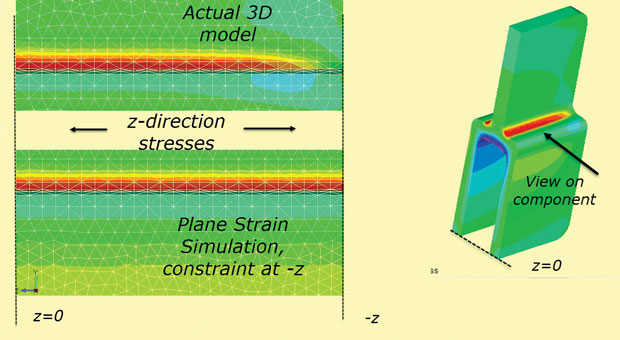Fig. 10: Diffusjon av z-stress mot den frie overflaten.

Rask Og Effektiv

fly stress og fly belastning analyser er nyttige 2d-metoder som ofte kan supplere fullskala 3d-modeller. Ikke alle funksjoner kan representeres, men med litt oppfinnsomhet kan stress på viktige områder i det minste estimeres. Motivasjonen for å bruke metodene er å muliggjøre rask effektiv analyse med enkel 2d geometri og mesh konstruksjon.