Grådig Algoritme Med Eksempler: Grådig Metode Og Tilnærming

for å forstå den grådige tilnærmingen må du ha arbeidskunnskap om rekursjon og kontekstveksling. Dette hjelper deg å forstå hvordan du sporer koden. Du kan definere det grådige paradigmet når det gjelder dine egne nødvendige og tilstrekkelige uttalelser.

To betingelser definerer det grådige paradigmet.

• hver trinnvis løsning må strukturere et problem mot sin best aksepterte løsning.
• det er tilstrekkelig hvis strukturen av problemet kan stoppe i et begrenset antall grådige trinn.

med teoretiseringen fortsatte, la oss beskrive historien knyttet Til Den Grådige søketilnærmingen.

I Denne Grådige algoritmen opplæringen, vil du lære:

• Historie Av Grådige Algoritmer
• Grådige Strategier Og Beslutninger
• Kjennetegn Ved Den Grådige Tilnærmingen
• hvorfor bruke Den Grådige Tilnærmingen?
• Hvordan Løse aktivitetsvalgproblemet
• Arkitektur Av Den Grådige tilnærmingen
• Ulemper Med Grådige Algoritmer

Historie Av Grådige Algoritmer

her er et viktig landemerke for grådige algoritmer:

• Grådige algoritmer ble konseptualisert for mange graf walk algoritmer på 1950-tallet.
• Esdger Djikstra konseptualisert algoritmen for å generere minimal spenner trær. Han hadde som mål å forkorte rutenettet i Den nederlandske hovedstaden Amsterdam.
• I samme tiår oppnådde Prim og Kruskal optimaliseringsstrategier som var basert på å minimere banekostnader langs veide ruter.
• På 70-tallet foreslo Amerikanske forskere, Cormen, Rivest og Stein en rekursiv understruktur av grådige løsninger i sin klassiske introduksjon til algoritmebok.
• Det Grådige søkeparadigmet ble registrert som en annen type optimaliseringsstrategi i nist-postene i 2005.
• protokoller som kjører nettet, for eksempel OPEN-shortest-path-first (ospf) og mange andre nettverkspakker, bruker den grådige strategien For å minimere tid brukt på et nettverk.

Grådige Strategier Og Beslutninger

Logikk i sin enkleste form ble kokt ned til «grådig» eller «ikke grådig». Disse uttalelsene ble definert av tilnærmingen tatt for å fremme i hvert algoritmetrinn.

for Eksempel brukte Djikstras algoritme en trinnvis grådig strategi som identifiserer verter på Internett ved å beregne en kostnadsfunksjon. Verdien som returneres av kostnad-funksjonen, fastslår om neste bane er «grådig » eller»ikke-grådig».

kort sagt, en algoritme slutter å være grådig hvis den på noe tidspunkt tar et skritt som ikke er lokalt grådig. De Grådige problemene stopper uten ytterligere omfang av grådighet.

Kjennetegn Ved Den Grådige Tilnærmingen

de viktige egenskapene til En Grådig metodealgoritme er:

• det er en bestilt liste over ressurser, med kostnader eller verdiattribusjoner. Disse kvantifiserer begrensninger på et system.
• du vil ta maksimalt antall ressurser i den tiden en begrensning gjelder.
• for eksempel i et aktivitetsplanleggingsproblem er ressurskostnadene i timer, og aktivitetene må utføres i seriell rekkefølge.

Hvorfor bruke Den Grådige Tilnærmingen?

her er grunnene til å bruke den grådige tilnærmingen:

• den grådige tilnærmingen har noen avvik, noe som kan gjøre den egnet for optimalisering.
• en fremtredende grunn er å oppnå den mest gjennomførbare løsningen umiddelbart. I aktivitetsvalgproblemet (Forklart nedenfor), hvis flere aktiviteter kan gjøres før du fullfører gjeldende aktivitet, kan disse aktivitetene utføres samtidig.
• En annen grunn er å dele et problem rekursivt basert på en betingelse, uten å måtte kombinere alle løsningene.
• i aktivitetsvalgproblemet oppnås «rekursiv divisjon» – trinnet ved å skanne en liste over elementer bare en gang og vurdere bestemte aktiviteter.

Slik Løser du aktivitetsvalgproblemet

i aktivitetsplanleggingseksemplet er det en «start» – og «slutt» – tid for hver aktivitet. Hver Aktivitet er indeksert av et tall for referanse. Det er to aktivitetskategorier.

1. betraktet aktivitet: Er Aktiviteten, som er referansen hvorfra evnen til å gjøre mer enn en gjenværende Aktivitet analyseres.
2. gjenstående aktiviteter: aktiviteter på en eller flere indekser foran den aktuelle aktiviteten.

den totale varigheten gir kostnaden for å utføre aktiviteten. Det er (finish-start) gir oss varigheten som kostnaden for en aktivitet.

du vil lære at den grådige omfanget er antall gjenværende aktiviteter du kan utføre i løpet av en vurdert aktivitet.

Arkitekturen Til Den Grådige tilnærmingen

TRINN 1)

Skann listen over aktivitetskostnader, og Start med indeks 0 som den vurderte Indeksen.

TRINN 2)

når flere aktiviteter kan være ferdig innen den vurderte aktiviteten er ferdig, begynner du å søke etter en eller flere gjenstående aktiviteter.

TRINN 3)

hvis det ikke er flere gjenstående aktiviteter, blir gjeldende gjenstående aktivitet den neste vurderte aktiviteten. Gjenta trinn 1 og trinn 2, med den nye vurderte aktiviteten. Hvis det ikke er noen gjenværende aktiviteter igjen, går du til trinn 4.

TRINN 4)

Returner foreningen av vurderte indekser. Dette er aktivitetsindeksene som skal brukes til å maksimere gjennomstrømning.

Kode Forklaring

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

forklaring av kode:

1. inkludert header filer / klasser
2. et maks antall aktiviteter levert av brukeren.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

forklaring av kode:

1. navneområdet for strømmeoperasjoner.
2. en klassedefinisjon for TID
3. et timestempel.
4. EN standardkonstruktør
5. variabelen timer.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

forklaring av kode:

1. en klassedefinisjon fra aktivitet
2. Tidsstempler som definerer en varighet
3. alle tidsstempler initialiseres til 0 i standardkonstruktøren

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

forklaring av kode:

1. Del 1 av scheduler class definition.
2. Betraktet Indeks er utgangspunktet for skanning av matrisen.
3. initialiseringsindeksen brukes til å tildele tilfeldige tidsstempler.
4. en rekke aktivitetsobjekter tildeles dynamisk ved hjelp av den nye operatoren.
5. den planlagte pekeren definerer gjeldende baseplassering for grådighet.

Scheduler(){ considered_index = 0; scheduled = NULL;......

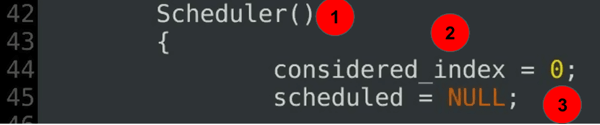
forklaring av kode:

1. the scheduler constructor-del 2 av scheduler klasse definisjon.
2. den vurderte indeksen definerer gjeldende start av gjeldende skanning.
3. den nåværende grådige omfanget er udefinert i starten.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

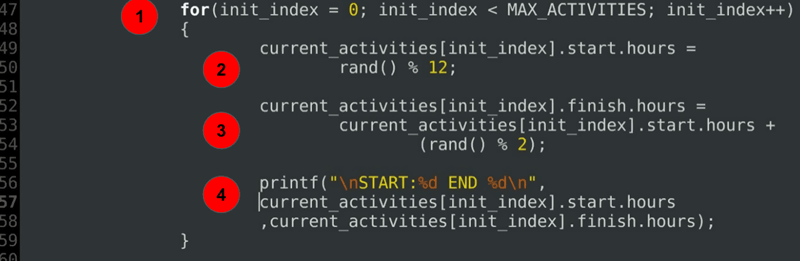
forklaring av kode:

1. a for loop for å initialisere starttimer og sluttimer for hver av de planlagte aktivitetene.
2. initialisering Av starttid.
3. Initialisering Av Sluttid alltid etter eller nøyaktig i starttimen.
4. en debug-setning for å skrive ut tildelte varigheter.

public: Activity * activity_select(int);};

forklaring av kode:

1. Del 4 – den siste delen av scheduler class definition.
2. Activity select-funksjonen tar en startpunktindeks som base og deler den grådige søken i grådige delproblemer.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. ved hjelp av scope resolution operator (::), er funksjonsdefinisjonen gitt.
2. den vurderte Indeksen er Indeksen kalt etter verdi. Greedy_extent er den initialiserte bare en indeks etter den vurderte Indeksen.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

forklaring av kode:

1. kjernen logikk-den grådige omfanget er begrenset til antall aktiviteter.
2. starttidene for den gjeldende Aktiviteten kontrolleres som planlagt før den vurderte Aktiviteten (gitt av vurdert indeks) avsluttes.
3. så lenge dette er mulig, skrives en valgfri debug-setning ut.
4. Gå videre til neste indeks i aktivitetsarrayen

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

forklaring av kode:

1. de betingede sjekker om alle aktivitetene er dekket.
2. Hvis ikke, kan du starte din grådige med den vurderte Indeksen som gjeldende punkt. Dette er et rekursivt trinn som grådig deler problemstillingen.
3. hvis Ja, går den tilbake til den som ringer uten mulighet for å utvide grådighet.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

forklaring av kode:

1. hovedfunksjonen som brukes til å påkalle planleggeren.
2. en ny Planlegger startes.
3. aktivitetsvelg-funksjonen, som returnerer en peker av typen aktivitet, kommer tilbake til den som ringer etter at den grådige søken er over.

Utgang:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

Ulemper Med Grådige Algoritmer

det er ikke egnet For Grådige problemer der en løsning er nødvendig for hvert delproblem som sortering.

I Slike Grådige algoritmeproblemer kan Den Grådige metoden være feil; i verste fall føre til en ikke-optimal løsning.

derfor bruker ulempen med grådige algoritmer ikke å vite hva som ligger foran den nåværende grådige staten.

Nedenfor er en skildring av ulempen med Den Grådige metoden:

i den grådige skanningen som vises her som et tre (høyere verdi høyere grådighet), vil en algoritmetilstand til verdi: 40, sannsynligvis ta 29 som neste verdi. Videre slutter sin søken på 12. Dette utgjør en verdi på 41.

men hvis algoritmen tok en suboptimal bane eller vedtok en erobringsstrategi. deretter vil 25 bli etterfulgt av 40, og den totale kostnadsforbedringen vil være 65, som er verdsatt 24 poeng høyere som en suboptimal beslutning.

Eksempler På Grådige Algoritmer

de fleste nettverksalgoritmer bruker den grådige tilnærmingen. Her er en liste over Noen Grådige algoritme eksempler:

• Prim Er Minimal Spenner Treet Algoritme
• Reiser Selger Problem
• Graf – Kart Coloring
• Kruskal Er Minimal Spenner Treet Algoritme
• Dijkstra Minimal Spenner Treet Algoritme
• Graf – Vertex Cover
• ryggsekk problem
• Jobb Planlegging Problem

Sammendrag:

For Å Oppsummere, Artikkelen Definert Grådig Paradigmet, Viste Hvordan Grådig Optimalisering Og Rekursjon, kan hjelpe Deg Å Få Den Beste Løsningen Opp Til Et Punkt. Den Grådige algoritmen er mye tatt i bruk for problemløsning på mange språk Som Grådig algoritme Python, C, C#, PHP,Java, etc. Aktiviteten utvalg Av Grådig algoritme eksempel ble beskrevet som et strategisk problem som kan oppnå maksimal gjennomstrømning ved hjelp av grådig tilnærming. Til slutt ble demerits av bruken av den grådige tilnærmingen forklart.