Jeg har begynt Å gjøre Andrew Ngs populære maskinlæringskurs På Coursera. Den første uken dekker mye, i hvert fall for noen som ikke har rørt mye kalkulator i noen år
- Kostnadsfunksjoner (gjennomsnittlig forskjell kvadrert)
- Gradient Descent
- Lineær Regresjon
Disse tre emnene var mye å ta inn. Jeg skal snakke om hver i detalj, og hvordan de alle passer sammen, med noen python-kode for å demonstrere.
Rediger 4. Mai: Jeg publiserte en oppfølging med fokus på hvordan Kostnadsfunksjonen fungerer her, inkludert en intuisjon, hvordan man beregner den for hånd og to forskjellige Python-implementeringer. Jeg kan gjøre gradient nedstigning og deretter bringe dem sammen for lineær regresjon snart.
Modellrepresentasjon
for det Første er målet med de fleste maskinlæringsalgoritmer å konstruere en modell: en hypotese som kan brukes Til å estimere Y basert På X. hypotesen, eller modellen, kartlegger innganger til utganger. Så, for eksempel, si at jeg trener en modell basert på en haug med boligdata som inkluderer størrelsen på huset og salgsprisen. Ved å trene en modell kan jeg gi deg et estimat på hvor mye du kan selge huset ditt for basert på størrelsen. Dette er et eksempel på et regresjonsproblem — gitt noen innspill, vil vi forutsi en kontinuerlig utgang.
hypotesen presenteres vanligvis som

theta-verdiene er parametrene.
noen raske eksempler på hvordan vi visualiserer hypotesen:
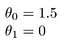
dette gir h(x) = 1,5 + 0x. 0x betyr ingen helling, og y vil alltid være konstant 1.5. Dette ser ut som:

hva med
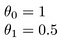

målet med å lage en modell er å velge parametere, eller theta-verdier, slik at h (x) er nær y for treningsdataene, x og y. Så for disse dataene
x =
y =

jeg vil prøve å finne en linje med best passform ved hjelp av lineær regresjon. La oss komme i gang.
Kostnadsfunksjon
Vi trenger en funksjon som vil minimere parametrene over datasettet vårt. En vanlig funksjon som ofte brukes er mean squared error, som måler forskjellen mellom estimatoren (datasettet) og den estimerte verdien (prediksjonen). Det ser slik ut:

det viser seg at vi kan justere ligningen litt for å gjøre beregningen nedover sporet litt enklere. Vi ender opp med:
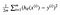
la oss bruke denne const-funksjonen til følgedataene:

For nå vil vi beregne noen theta-verdier, og plotte kostnadsfunksjonen for hånd. Siden denne funksjonen går gjennom (0, 0), ser vi bare på en enkelt verdi av theta. Herfra vil jeg referere Til kostnadsfunksjonen Som J (Θ).
For J (1) får vi 0. Ingen overraskelse – en verdi På J (1) gir en rett linje som passer perfekt til dataene. Hva med J (0,5)?

MSE-funksjonen gir oss en verdi på 0,58. La oss plotte begge våre verdier så langt:
J(1) = 0
J(0,5) = 0.58

jeg vil gå videre og beregne noen flere verdier Av J (Θ).

Og hvis vi blir med prikkene sammen pent…

vi kan se at kostnadsfunksjonen er på et minimum når theta = 1. Dette er fornuftig — våre opprinnelige data er en rett linje med en skråning på 1 (den oransje linjen i figuren ovenfor).
Gradient Descent
vi minimerte J(Θ) ved prøving og feiling over-bare prøver mange verdier og visuelt inspiserer den resulterende grafen. Det må være en bedre måte? Kø gradient nedstigning. Gradient Descent er en generell funksjon for å minimere en funksjon, i dette tilfellet Mean Squared Error cost-funksjonen.
Gradient Descent gjør i utgangspunktet bare det vi gjorde for hånd-endre theta-verdiene, eller parametrene, bit for bit, til vi forhåpentligvis kom et minimum.
vi starter med å initialisere theta0 og theta1 til noen to verdier, si 0 for begge, og gå derfra. Formelt er algoritmen som følger:

hvor α, alfa, er læringsraten, eller hvor raskt vi vil bevege oss mot minimum. Hvis α er for stort, kan vi imidlertid overskride.

Bringe det hele sammen-Lineær Regresjon
raskt oppsummering:
Vi har en hypotese:

som vi trenger passer til våre treningsdata. Vi kan bruke en kostnad funksjon Slik Middel Kvadrat Feil:

som vi kan minimere ved hjelp av gradient descent:

som fører oss til vår første maskinlæringsalgoritme, lineær regresjon. Det siste stykket av puslespillet vi må løse for å ha en fungerende lineær regresjonsmodell er partielt derivat av kostnadsfunksjonen:
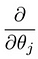
Som viser seg å være:
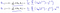
Som gir oss lineær regresjon!
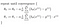
med teorien ut av veien, fortsetter jeg å implementere denne logikken i python i neste innlegg.
Rediger 4. Mai: jeg publiserte en oppfølging med fokus på Hvordan Kostnadsfunksjonen fungerer her, inkludert en intuisjon, hvordan man beregner den for hånd og to forskjellige Python-implementeringer. Jeg kan gjøre gradient nedstigning og deretter bringe dem sammen for lineær regresjon snart.