Husholdertransformasjon
Husholdertransformasjon (også «Husholderrefleksjon») er en ortogonal refleksjonstransformasjon:
- det reflekterer vektorene i kolonnene i matrisen slik at
- den første vektoren har alle nuller unntatt det første elementet
Transformasjonsmatrisen
Refleksjonstransformasjon:
Egenskaper
Husholdningsmatriser er symmetriske og ortogonale: de er refleksjon matriser
Derivasjon
så vi har $P = I – 2vv^t$:
vi bruker slike transformasjoner for nullstillingselementer
QR-Dekomponering
som I TILFELLE Lu-Dekomponering, hvor vi brukte en rekke Gauss-Transformasjonsendringer, kan vi gjøre det samme og utføre en serie Husholdertransformasjoner
- så hvis vi velger $y = \pm e_1$ (hvor $e_1$ er matrisen med 1 på posisjon 1 og resten er nuller)
- vil det nullere alle elementer av $x$ unntatt den første
- Dermed Ved Riktig Valg av $h$ kan vi ta $a$ og null alle Underdiagonalene elementer
- kan gjøre det flere ganger for hver kolonne på $A$
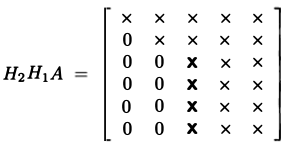
på denne måten kan VI utføre QR-Dekomponering:
Hessenberg Dekomponering
I Stedet for å bruke den til å redusere matrisen Til Trekantet, kan Vi bruke Husholderstransformasjon for å redusere en matrise Til Hessenbergmatrise