het vinden van een optimale oplossing voor bepaalde optimalisatieproblemen kan een ongelooflijk moeilijke taak zijn, vaak praktisch onmogelijk. Dit komt omdat wanneer een probleem voldoende groot wordt, we een enorm aantal mogelijke oplossingen moeten zoeken om de optimale te vinden. Zelfs met moderne rekenkracht zijn er nog vaak te veel mogelijke oplossingen te overwegen. In dit geval, omdat we realistisch gezien niet kunnen verwachten de optimale te vinden binnen een redelijke tijd, moeten we genoegen nemen met iets dat dichtbij genoeg is.
een voorbeeld van een optimalisatieprobleem dat gewoonlijk een groot aantal mogelijke oplossingen biedt, is het probleem van de reizende verkoper. Om een oplossing te vinden voor een probleem zoals het reizende verkoper probleem moeten we een algoritme gebruiken dat in staat is om een goede oplossing te vinden in een redelijke hoeveelheid tijd. In een vorige tutorial bekeken we hoe we dit konden doen met genetische algoritmen, en hoewel genetische algoritmen een manier zijn om een ‘goed-genoeg’ oplossing te vinden voor het probleem van de reizende verkoper, zijn er andere eenvoudigere algoritmen die we kunnen implementeren die ons ook een bijna optimale oplossing zullen vinden. In deze tutorial gebruiken we het algoritme ‘gesimuleerde gloeien’.
Als u niet bekend bent met het probleem van de reizende verkoper, is het misschien de moeite waard om mijn vorige tutorial te bekijken voordat u verder gaat.
Wat is gesimuleerd gloeien?
laten we eerst eens kijken hoe gesimuleerde gloeiing werkt, en waarom het goed is in het vinden van oplossingen voor het probleem van de reizende verkoper in het bijzonder. Het gesimuleerde gloeialgoritme is oorspronkelijk geïnspireerd op het proces van gloeien in metaalbewerking. Het ontharden impliceert het verwarmen en koelen van een materiaal om zijn fysische eigenschappen toe te schrijven aan de veranderingen in zijn interne structuur te veranderen. Naarmate het metaal afkoelt, wordt de nieuwe structuur vastgezet, waardoor het metaal zijn nieuw verkregen eigenschappen behoudt. Bij gesimuleerd gloeien houden we een temperatuurvariabele om dit verwarmingsproces te simuleren. We zetten het in eerste instantie hoog en laten het dan langzaam ‘afkoelen’ terwijl het algoritme loopt. Hoewel deze temperatuurvariabele hoog is, zal het algoritme, met meer frequentie, oplossingen accepteren die slechter zijn dan onze huidige oplossing. Dit geeft het algoritme de mogelijkheid om te springen uit elke lokale optimums het zich bevindt in het begin van de uitvoering. Naarmate de temperatuur daalt, is de kans op het accepteren van slechtere oplossingen, waardoor het algoritme zich geleidelijk kan richten op een gebied van de zoekruimte waarin hopelijk een bijna optimale oplossing kan worden gevonden. Dit geleidelijke ‘koeling’ proces is wat het gesimuleerde gloeialgoritme opmerkelijk effectief maakt bij het vinden van een bijna optimale oplossing bij het omgaan met grote problemen die tal van lokale optimums bevatten. De aard van de reizende verkoper probleem maakt het een perfect voorbeeld.
voordelen van gesimuleerd gloeien
u vraagt zich misschien af of er werkelijk voordelen zijn aan het toepassen van gesimuleerd gloeien over iets als een eenvoudige bergbeklimmer. Hoewel bergbeklimmers verrassend effectief kunnen zijn in het vinden van een goede oplossing, hebben ze ook de neiging om vast te komen te zitten in lokale optimums. Zoals we eerder bepaald, is het gesimuleerde gloeialgoritme uitstekend in het vermijden van dit probleem en is gemiddeld veel beter in het vinden van een geschatte globale optimum.
om een beter inzicht te krijgen, laten we snel een kijkje nemen naar waarom een basis bergbeklimmen algoritme zo gevoelig is om gevangen te raken in lokale optimums.
een algoritme voor bergbeklimmers accepteert eenvoudigweg oplossingen die beter zijn dan de huidige oplossing. Als de bergbeklimmer geen betere buren kan vinden, stopt het.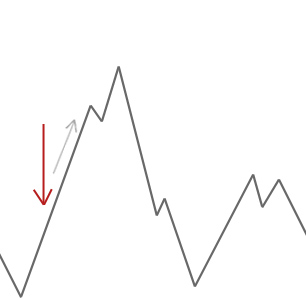
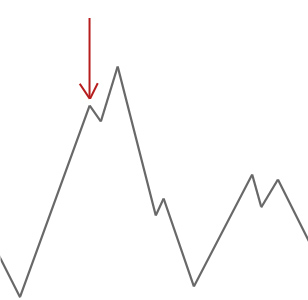
in het voorbeeld hierboven beginnen we onze bergbeklimmer bij de rode pijl en hij gaat de heuvel op tot hij een punt bereikt waar hij niet hoger kan klimmen zonder eerst af te dalen. In dit voorbeeld kunnen we duidelijk zien dat het vast zit in een lokaal optimum. Als dit een echt wereldprobleem zou zijn zouden we niet weten hoe de zoekruimte eruit ziet, dus helaas zouden we niet in staat zijn om te zeggen of deze oplossing ergens in de buurt van een globaal optimum is.
gesimuleerde gloeiing werkt iets anders dan dit en zal af en toe slechtere oplossingen accepteren. Dit kenmerk van gesimuleerde gloeien helpt het om te springen uit een lokale optimums zou het anders vast komen te zitten.
Acceptatiefunctie
laten we eens kijken hoe het algoritme bepaalt welke oplossingen te accepteren, zodat we beter kunnen begrijpen hoe het in staat is om deze lokale optimums te vermijden.
eerst controleren we of de buuroplossing beter is dan onze huidige oplossing. Als dat zo is, accepteren we het onvoorwaardelijk. Als de buuroplossing echter niet beter is, moeten we een aantal factoren in overweging nemen. Ten eerste, hoeveel erger de buuroplossing is; en ten tweede, hoe hoog de huidige ’temperatuur’ van ons systeem is. Bij hoge temperaturen accepteert het systeem eerder oplossingen die slechter zijn.
de wiskunde hiervoor is vrij eenvoudig:
hoe kleiner de verandering in energie (de kwaliteit van de oplossing), en hoe hoger de temperatuur, hoe waarschijnlijker het is dat het algoritme de oplossing accepteert.
algoritme overzicht
Hoe ziet het algoritme eruit? Nou, in zijn meest elementaire implementatie is het vrij eenvoudig.
- eerst moeten we de begintemperatuur instellen en een willekeurige beginoplossing maken.
- dan beginnen we met loopen totdat aan onze stopvoorwaarde is voldaan. Meestal is het systeem voldoende afgekoeld of is er een goede oplossing gevonden.
- hier selecteren we een buur door een kleine wijziging aan te brengen in onze huidige oplossing.
- dan beslissen we of we naar die buuroplossing gaan.
- ten slotte verlagen we de temperatuur en gaan we verder met lus
Temperatuurinitialisatie
voor een betere optimalisatie moeten we bij het initialiseren van de temperatuurvariabele een temperatuur kiezen die in eerste instantie vrijwel elke beweging tegen de huidige oplossing mogelijk maakt. Dit geeft het algoritme de mogelijkheid om de gehele zoekruimte beter te verkennen voordat het afkoelt en zich in een meer gericht gebied vestigt.
voorbeeld Code
laten we nu gebruiken wat we weten om een basis gesimuleerd gloeialgoritme te maken, en dan toepassen op de reizende verkoper probleem hieronder. We gaan Java gebruiken in deze tutorial, maar de logica moet hopelijk eenvoudig genoeg zijn om te kopiëren naar een taal van uw keuze.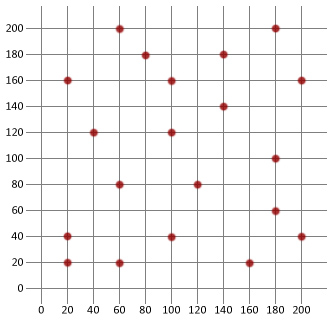
eerst moeten we een Stadsklasse creëren die kan worden gebruikt om de verschillende bestemmingen van onze reizende verkoper te modelleren.
stad.java
* stad.java
* Models a city
* /
package sa;
public class City {
int x;
int y;
/ / construeert een willekeurig geplaatste stad
public City () {
this.x = (Int) (Math.random () * 200);
dit.y = (Int) (Math.willekeurig()*200);
}
// construeert een stad op gekozen x, Y locatie
openbare stad (int x, int y){
dit.x = x;
dit.y = y;
}
// krijgt de x-coördinaat van de stad
public int getX () {
geef dit terug.x;
}
// krijgt de Y-coördinaat van de stad
public int getY () {
geef dit terug.y;
}
// geeft de afstand tot een gegeven stad
publieke dubbele afstand(City city){
Int xDistance = Math.abs (getX () – city.getX ());
int yDistance = Math.abs (getY () – stad.getY ());
dubbele afstand = wiskunde.sqrt ((xDistance*xDistance) + (yDistance*yDistance) );
return distance;
}
@Override
public String toString () {
return getX ()+”, ” +getY();
}
}
laten we vervolgens een klasse creëren die de steden kan bijhouden.
TourManager.java
* TourManager.java
* bevat de steden van een tour
* /
package sa;
import java.util.ArrayList;
Public class TourManager {
/ / Holds our cities
private static ArrayList destinationCities = new ArrayList<City>();
// voegt een bestemmingsstad
public static void addCity (City city) {
destinationCities toe.toevoegen (stad));
}
// Get a city
public static City getCity (int index){
return (City) destinationCities.get (index));
}
// haal het aantal bestemmingssteden
public static int numberOfCities () {
return destinationCities.grootte();
}
}
nu om de klasse te creëren die een reizende verkoper tour kan modelleren.
Tour.java
* Tour.java
* slaat een candidate tour op door alle steden
* /
package sa;
import java.util.ArrayList;
java importeren.util.Collections;
public class Tour{
/ / Holds our tour of cities
private ArrayList tour = new ArrayList<City>();
// Cache
private int distance = 0;
/ / maakt een lege tour
public Tour(){
voor (Int i = 0; i < TourManager.numberOfCities (); i++) {
tour.toevoegen (null);
}
}
// maakt een tour van een andere tour
openbare Tour(ArrayList tour){
dit.tour = (ArrayList) tour.klonen();
}
// retourneren tour informatie
public ArrayList getTour () {
retourneren tour;
}
// maakt een willekeurige individuele
public void generateIndividual () {
/ / Loop door al onze bestemmingen en voeg ze toe aan onze tour
voor (int cityIndex = 0; cityIndex < TourManager.numberOfCities (); cityIndex++) {
setCity (cityIndex, TourManager.getCity(cityIndex)));
}
// de volgorde van de collecties van de tour
willekeurig wijzigen.shuffle (tour);
}
// krijgt een stad uit de tour
public City getCity (int tourPosition) {
return (City)tour.get(tourpositie));
}
// zet een stad in een bepaalde positie binnen een tour
openbare ruimte setCity (int tourPosition, City city) {
tour.set (tourPosition, city);
// als de tours zijn gewijzigd, moeten we de conditie en afstand
resetten = 0;
}
// geeft de totale afstand van de tour
public int getDistance () {
if (distance == 0) {
int tourDistance = 0;
/ / Loop door de steden van onze tour
voor (int cityIndex=0); cityIndex < tourSize(); cityIndex++) {
// Voor stad we reizen van
Stad fromCity = getCity(cityIndex);
// City-we reizen naar
Stad destinationCity;
// Controleren we niet op onze tour de laatste stad, als we onze
// tour de uiteindelijke bestemming van de stad om ons te beginnen stad
als(cityIndex+1 < tourSize()){
destinationCity = getCity(cityIndex+1);
}
else{
destinationCity = getCity(0);
}
// Voor de afstand tussen de twee steden
tourDistance += fromCity.distanceTo (destinationCity);
}
distance = tourDistance;
}
retourafstand;
}
// Get aantal steden op onze tour
public int tourSize () {
retour tour.grootte();
}
@Override
public String toString () {
String geneString=|/”;
for (int i = 0; i < tourSize(); i++) {
geneString += getCity (i)+”|”;
}
geneString retourneren;
}
}
laten we tenslotte ons gesimuleerde gloeialgoritme maken.
gesimuleerde gloeilamp.java
openbare klasse gesimuleerde gloeidraad {
/ / Bereken de aanvaardingskans
openbare statische dubbele aanvaardbaarheid (int energie, int nieuwe energie, Dubbele temperatuur) {
/ / indien de nieuwe oplossing beter is, accepteer deze
indien (nieuwe energie < energie) {
retour 1.0;
}
// als de nieuwe oplossing slechter is, bereken dan een acceptatiekans
return Math.exp ((energy-newEnergy) / temperature);
}
public static void main(String args) {
// Create and add our cities
City city = new City(60, 200);
TourManager.addCity (stad);
stad stad2 = nieuwe stad (180, 200);
TourManager.addCity (city2);
City city3 = new City(80, 180);
TourManager.addCity (city3);
City city4 = new City(140, 180);
TourManager.addCity (city4);
City city5 = new City(20, 160);
TourManager.addCity (city5);
City city6 = new City(100, 160);
TourManager.addCity (city6);
City city7 = new City(200, 160);
TourManager.addCity (city7);
City city8 = new City(140, 140);
TourManager.addCity (city8);
City city9 = new City(40, 120);
TourManager.addCity (stad9);
stad stad10 = nieuwe stad(100, 120);
TourManager.addCity (city10);
City city11 = new City(180, 100);
TourManager.addCity (city11);
City city12 = new City(60, 80);
TourManager.addCity (city12);
City city13 = new City(120, 80);
TourManager.addCity (city13);
City city14 = new City(180, 60);
TourManager.addCity (city14);
City city15 = new City(20, 40);
TourManager.addCity (city15);
City city16 = new City(100, 40);
TourManager.addCity (city16);
City city17 = new City(200, 40);
TourManager.addCity(stad17);
stad city18 = new City (20, 20);
TourManager.addCity (city18);
City city19 = new City(60, 20);
TourManager.addCity (city19);
City city20 = new City(160, 20);
TourManager.addCity (city20);
// set initial temp
double temp = 10000;
// Cooling rate
double coolingRate = 0,003;
// Initialize intial solution
Tour currentSolution = new Tour ();
currentSolution.generateIndividual ();
systeem.uit.println (“Initial solution distance:” + currentSolution.getDistance ());
/ / Stel in als huidige beste
Tour best = nieuwe Tour (currentSolution.getTour());
// Loop totdat het systeem is afgekoeld
terwijl (temp > 1) {
// Maak een nieuwe neighbour tour
Tour newSolution = new Tour (currentSolution.getTour ());
/ / krijg een willekeurige positie in de tour
int tourPos1 = (int) (newSolution.tourSize () * Math.random ());
int tourPos2 = (int) (newSolution.tourSize () * Math.random ());
/ / haal de steden op geselecteerde posities in de tour
City citySwap1 = newSolution.getCity (tourPos1);
City citySwap2 = newSolution.getCity (tourPos2);
// Swap ze
newSolution.setCity (tourPos2, citySwap1);
newSolution.setCity (tourPos1, citySwap2);
// Get energy of solutions
int currentEnergy = currentSolution.getDistance ();
int neighbourEnergy = newSolution.getDistance();
// bepaal of we de buurman
moeten accepteren if (acceptanceProbability(currentEnergy, neighbourEnergy, temp) > Math.random()) {
currentSolution = new Tour (newSolution.getTour());
}
// Houd de beste gevonden oplossing
if (currentSolution.getDistance () < best.getDistance()) {
best = new Tour (currentSolution.getTour());
}
// Koelsysteem
temp * = 1-koelsnelheid;
}
systeem.uit.println (“final solution distance:” + best.getDistance());
systeem.uit.println(“Tour:” + beste);
}
}
Output:
Definitieve oplossing afstand: 911 ‘Tour’: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
Conclusie
In dit voorbeeld hebben we in staat waren om meer dan de helft van de afstand van onze eerste willekeurig gegenereerde route. Dit laat hopelijk zien hoe handig dit relatief eenvoudige algoritme is wanneer het wordt toegepast op bepaalde soorten optimalisatieproblemen.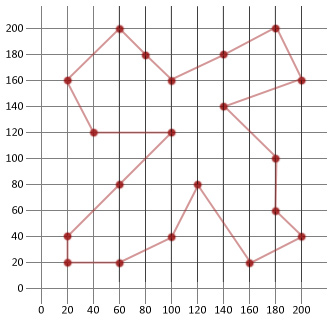
auteur
 Hallo, Ik Ben Lee.
Hallo, Ik Ben Lee.ik ben een ontwikkelaar uit het Verenigd Koninkrijk die van technologie en business houdt. Hier vindt u artikelen en tutorials over dingen die me interesseren. Als u me wilt inhuren of meer over me wilt weten, ga dan naar mijn Over me pagina