het elektrische veld E kan altijd worden uitgedrukt als de gradiënt van een scalaire potentiaal functie
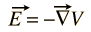
er is geen algemeen scalair potentieel voor magnetisch veld B, maar het kan worden uitgedrukt als de krul van een vectorfunctie
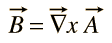
deze functie A krijgt de naam “vectorpotentiaal” maar het wordt niet direct geassocieerd met werk zoals scalairpotentiaal is.
het vectorpotentiaal wordt gedefinieerd als consistent met de wet van Ampère en kan worden uitgedrukt in termen van stroom i of stroomdichtheid j (de bronnen van het magnetisch veld). In verschillende teksten neemt deze definitie de vorm aan van
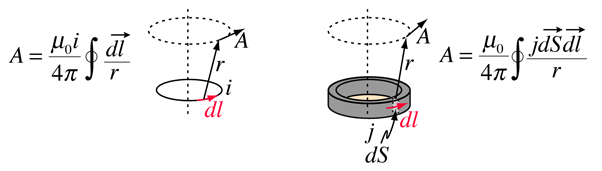
een reden voor het vectorpotentiaal is dat het gemakkelijker kan zijn om het vectorpotentiaal te berekenen dan om het magnetische veld rechtstreeks uit een gegeven bronstroomgeometrie te berekenen. De meest voorkomende toepassing is de antennetheorie en de beschrijving van elektromagnetische golven.
aangezien het magnetisch veld B is gedefinieerd als de krul van A en de door vectoridentiteit de krul van een gradiënt identiek nul is, mag elke willekeurige functie die kan worden uitgedrukt als de gradiënt van een scalaire functie aan A worden toegevoegd zonder de daaruit verkregen waarde van B te wijzigen. Dat wil zeggen, een ‘ kan vrij worden vervangen voor een waar
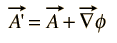
dergelijke transformaties worden maattransformaties genoemd,en er zijn een aantal “meters” die zijn gebruikt om te profiteren is specifieke soorten berekeningen in de elektromagnetische theorie.