Simplifying FEA Models: Plane Stress and Plane Strain

Noot van de redactie: Tony Abbey geeft live NAFEMS FEA lessen in de VS, Europa en Azië. Hij geeft ook NAFEMS e-learning lessen wereldwijd. Contact .voor details.In een eerder artikel over Desktop Engineering (“Simplify FEA Simulation Models Using Planar Symmetry”) werd uitgelegd dat zelfs met krachtige moderne computers, er vaak een motivatie is om simplifying techniques in structural finite element analysis (FEA) te gebruiken. Deze follow-up beschrijft hoe twee nauw verwante methoden kunnen worden gebruikt om 2D-plakken door een complexe structuur te nemen op gebieden van belang. De resulterende FEA-modellen kunnen sneller en efficiënter waardevol inzicht geven in lokale spanningen dan een volledig 3D-model. Ze vertellen niet het hele verhaal, maar zijn waardevolle hulpmiddelen voor de CAE-ingenieur.

de twee FEA-methoden worden vlakke spanning en vlakke spanning genoemd. Beide maken gebruik van 2D vlakke elementen die eruit zien als dunne schaalelementen en zijn fijnmazig met behulp van vlakke oppervlakgeometrie.

Vlakke Spanningsanalyse

Fig. 1 toont de belangrijke feiten over de analyse van vliegtuigstress. De structurele regio wordt verondersteld te liggen in het 2D xy vlak, met de derde structurele dimensie relatief klein. In de figuur is dit de dikte in de z-richting. Spanningen bestaan in het 2D-vlak als sigma x, sigma y (directe spanningen) en sigma xy (in-plane afschuifspanning). Elk van deze spanningen is constant door de dikte zoals aangegeven in de inzet. Bovendien kan er geen stress in de z-richting zijn. Deze relatie tussen spanning en spanning wordt gedefinieerd in 2D vlakke spanningselementen die in dit type analyse worden gebruikt.

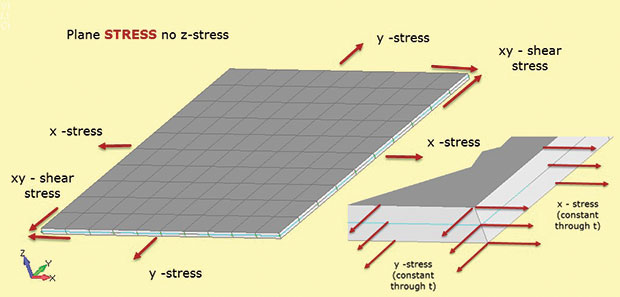Fig. 1: Plane stress; aannames over de stresstoestand.

het ontbreken van z-spanning is de manier om de aanduiding van het elementtype vlakke spanning te onthouden (dat wil zeggen dat alleen in-vlakke spanningen zijn toegestaan). Er zijn ook geen doordikteschuifspanningen. We kunnen het vliegtuig stress model in Fig. 1 met een bi-axiale belasting en bereken sigma x en sigma y. Er is geen sigma z. we kunnen ook de overeenkomstige in-plane stammen E-x en e-y berekenen. als we een schuifbelasting toepassen, kunnen we schuifspanning sigma xy en schuifspanning e-xy vinden. Interessant is dat we ook de doordikte Spanning e-z kunnen berekenen. dit is niet nul, omdat het model vrij is om te dunnen in z als het zich uitstrekt in x en y. er is geen Out-of-plane beperking om dit te voorkomen. In sommige solvers kunnen we de doordikte Spanning E-z recupereren en gebruiken om de verandering in dikte te berekenen. (Als het model in bi-axiale compressie is dan zal de Z-sectie dikker worden). Dit wordt meestal beschouwd als een secundaire stam en kan niet beschikbaar zijn voor output—maar het is er en kan handmatig worden berekend indien nodig.

Fig. 2 toont een aluminium lug component. De lug steekt uit een composiet vel layup die lagen gepositioneerd en gebonden over de tangs (of benen) en onderlichaamsectie heeft. De tangs brengen de belasting die op de lug wordt toegepast, over in de composietstructuur. In de praktijk zouden de lagen worden getrapt om een soepele afschuifoverdracht door de binding in het composiet mogelijk te maken. De afschuifoverdracht in het composiet wordt hier gesimuleerd door diffuse oppervlaktetractiekrachten “trekken” op de tangs. Deze balanceren de toegepaste lug belasting.

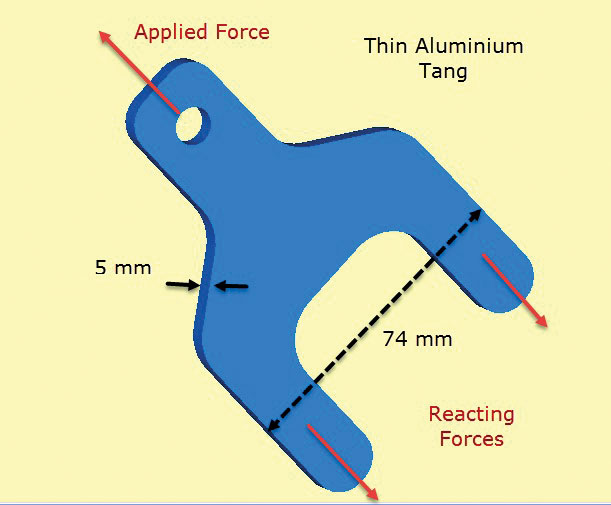Fig. 2: Dunwandige aluminium tang overdracht van lading in composiet structuur.

de belangrijkste aanname is dat de doordiktespanningen nul zijn en dat de in het vlak aanwezige spanningen constant zijn door de dikte van het onderdeel. Dit betekent dat het lokale detail van de afschuifbelasting van composiet naar tang slecht gemodelleerd is. Echter de focus van deze analyse is om de grootte van lug en tang doorsnede vrij van de composiet te controleren, met behulp van in-vlakke spanningen.

de dikte van het onderdeel is klein in vergelijking met andere afmetingen. Deze waarde wordt ingevoerd als de werkelijke dikte in de definitie van het vlakspanningselement.

Fig. 3 toont het FEA-model en de berekende maximale hoofdspanningen. De gebieden van belang zijn rond de lug en de schouder radii. In de echte wereld zou de spanningstoestand bij de spanningsconcentraties 3D zijn en door dikte zouden Sigma z spanningen en afschuifspanningen lokaal in balans zijn. Het is hier echter zeer redelijk om aan te nemen dat de spanningen in het vliegtuig domineren. Dit is dezelfde veronderstelling die impliciet aanwezig is in de meeste traditionele berekeningen van de stressconcentratie (kt) die in handboeken worden aangetroffen.

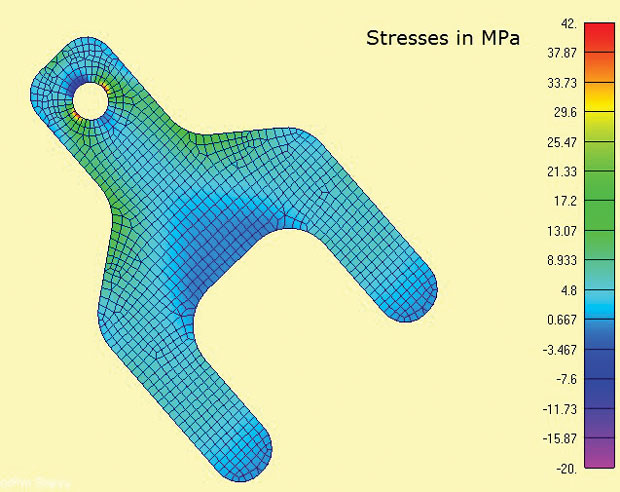Fig 3: 2D Vlakspanningselementen met maximale hoofdspanningen

een van de handige kenmerken van de vlakspanningsanalyse is dat het een strikt 2D-analyse is, zodat slechts drie vrijheidsgraden (dof) beperkt hoeven te worden (in-plane vertalingen x, y en rotatie om de Z-as). Dit leent zich voor de 3-2-1 minimum constraint methode met gebalanceerde belasting. In een 2D geval degenereert dit tot een 2-1 methode. Een knoop heeft DOF x en y beperkt, een tweede geschikte orthogonale knoop heeft dof x beperkt. Hierdoor kan de reactiebelasting in de tangs direct worden toegepast als diffuse balancerende belastingen. Het zou moeilijk zijn om deze grensvoorwaarde te simuleren via beperkingen aan de grond.

de doordikte E-z-stam en dus het verdunnen van de tangs kunnen als secundair effect worden berekend.

Vlakke Stamanalyse

Fig. 4 toont de essentie van de plane strain methode. Nogmaals, 2D vlakke elementen worden gebruikt, maar met subtiel verschillende veronderstellingen. De in-vliegtuig spanningen x, y en xy worden ontwikkeld als voorheen. Maar deze keer is het de out-of-plane, of door dikte z spanning die is ingesteld op nul. Dus vlakke stam analyse laat alleen stammen in-plane toe. Dit werkt goed om dikke structuren zoals weergegeven weer te geven. De aanwezigheid van dit veel materiaal heeft de neiging om de component te stabiliseren en te voorkomen dat het overspannen in z. dit betekent ook dat constante door dikte z spanningen worden ontwikkeld in de structuur. Deze spanning-rekmateriaal relatie wordt gedefinieerd in 2D vlakke rekelementen die in dit type analyse worden gebruikt.

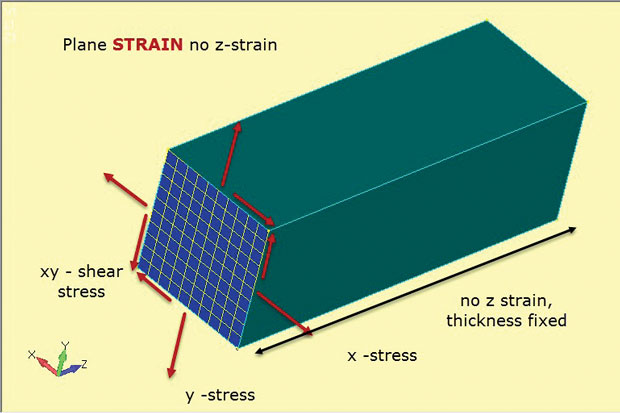Fig. 4: Plane strain analysis; stress en strain state veronderstellingen.

de figuur toont de oriëntatie van de Tweed-vlakke spanningselementen als een doorsnede door een typische diepe component. De aanname is dat de spanningstoestand op deze snijsectie zal worden gedupliceerd op elk XY vlak cut (Z station) door de component. De component wordt verondersteld prismatisch te zijn (met een constante doorsnede) over zijn lengte.

in de praktijk gebruiken we deze methode waarbij de spanningstoestand in een diepe component langzaam varieert van vlak tot vlak. Er moet genoeg materiaal door de diepte te stabiliseren en te elimineren van de door dikte stam. Dit is hetzelfde principe dat wordt toegepast op de in Fig. 5. Voor het middengedeelte van het dikke specimen wordt een storing onder vlakke drukomstandigheden getoond. De storing aan de vrije randen en het dunne gedeelte is een andere modus, meer als een vlakke spanningstoestand. Een plane strain FEA model zou per definitie een goede weergave zijn van het middenlijn Dikke specimen gedrag, maar niet van de vrije randen of het dunne specimen.

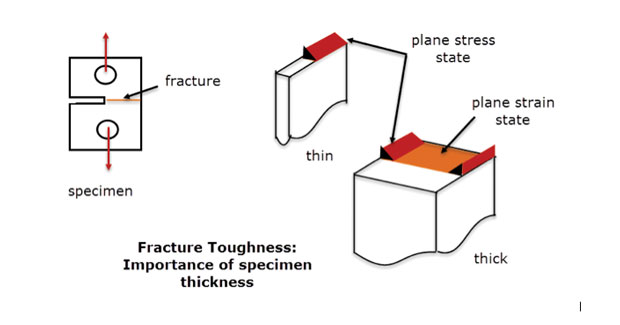Fig. 5: breuktaaiheid specimens; dunne en dikke secties.

Fig. 6 toont een andere component die wordt gebruikt in een composietstructuur, die een gebonden verbinding vormt. Hier is de sectie constant en diep genoeg zodat we kunnen aannemen dat de spanningen ook constant zijn met diepte. De vrije eindvlakken (bij +z, – z) zullen een andere lokale spanningstoestand hebben (eigenlijk vlakke spanning, zoals opgemerkt), maar het doel van deze analyse is om de netto sectiespanningen op de middellijn te controleren (z = 0).

de 2D vlakke strain analysis mesh is afgebeeld in de 3D-component in Fig. 7. De doorsnede wordt gedefinieerd bij station z = 0.

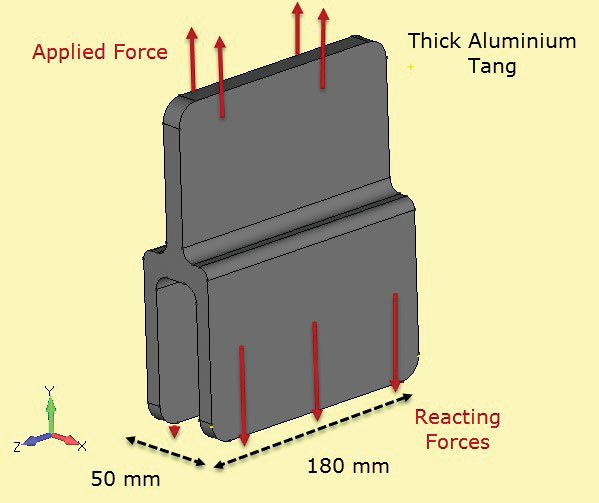Fig 6: aluminium tang.

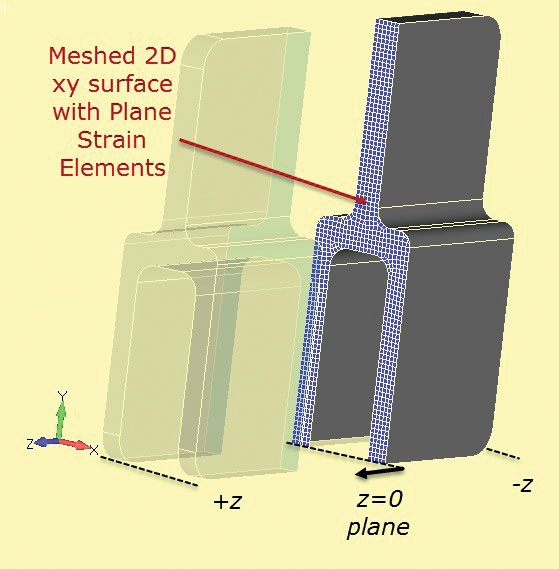Fig. 7: Sectie snijd door vaste sectie om 2D vlakke spanningssectie te ontwikkelen.

er kan een zeer fijn 2D-vlakgaas worden gebruikt, dat zeer snel zal werken in vergelijking met een volledig 3D-model. De 2-1 constraint methode wordt gebruikt als voorheen. De lading moet zorgvuldig worden overwogen. De “dikte” van de vlakke stam sectie is vrij willekeurig, en wordt meestal ingesteld op 1.0 standaard. Als de belasting op het onderdeel wordt berekend als een lopende belasting door de diepte (N/m, Lbf/inch enz.) dan kan deze waarde direct worden gebruikt op het vlak strain mesh. Het is nuttig om een sectie, zoals de enkele tang te kiezen en de nominale Of gemiddelde spanning in deze sectie voor de volledige component te schatten. Dit kan worden gebruikt als een sanity check in de vlakke stam analyse. Onjuist laden is waarschijnlijk de belangrijkste oorzaak van fout in deze methode.

de resultaten van de analyse zijn weergegeven in Fig. 8 en tonen duidelijk de gebieden van hoge stress rond de schouderfilet. De spanningen gelden voor het centrale dieptegebied van het onderdeel (z = 0).

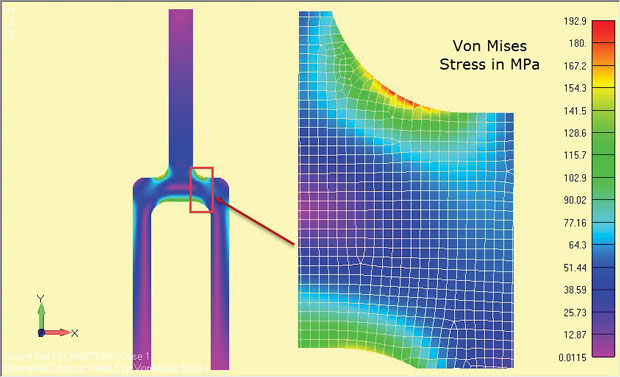Fig. 8: Vlakke stam analyseresultaten van een diepe tang component.

de gebruikte stresshoeveelheden zijn afhankelijk van de gebruikte oplosser. Sommige oplossers negeren de Z-richting spanningen als secundaire en herstellen de in-vliegtuig spanningen. De belangrijkste spanningen en von Mises spanningen hebben dan betrekking op een 2D in-vlakke spanningstoestand. Als de spanning in de z-richting wordt hersteld, moet deze duidelijk worden geïdentificeerd, zodat de 2D-spanningstoestand in het x-y-vlak kan worden geïdentificeerd.

wat vertegenwoordigt de Z-richtingsstress precies? Het is de spanning ontwikkeld als gevolg van de handhaving van nul Z richting spanning. De stress werkt alsof de vrije uiteinden van het prismatische gedeelte vast zijn. Op het centrale vlak van een diepe sectiecomponent zullen dit de complementaire spanningen zijn die nodig zijn om de nul-Z-richting-rektoestand vast te houden. In werkelijkheid als we bewegen naar de vrije oppervlakken, de Z-stress daalt tot nul en wordt een vlakke spanningsverdeling (zoals te zien in de dikke fractuur mechanica specimen).

in veel gevallen, zoals bij een drukcilinder, zijn de uiteinden afgedekt en zullen zij in feite een axiale belasting ontwikkelen als gevolg van axiale krachten. Dit zal een andere spanning zijn dan de geïnduceerde axiale spanning in de vlakke stamanalyse. Een handberekening zal nodig zijn om de axiale spanningen te berekenen, of eventueel een aanvullend axisymmetrisch model voor drukvaten.

het gemak van geometrie en mesh constructie leent zich goed voor “wat-als” studies of meer formele vorm optimalisatie studies.

ter vergelijking werd een half-symmetrie volledige 3D-analyse van de diepe tang-component uitgevoerd en de resultaten zijn weergegeven in Fig. 9. De nominale spanning over de bovenste enkele tangbeen is identiek in beide gevallen-vergeet niet dat dit de basis van elke sanity check.

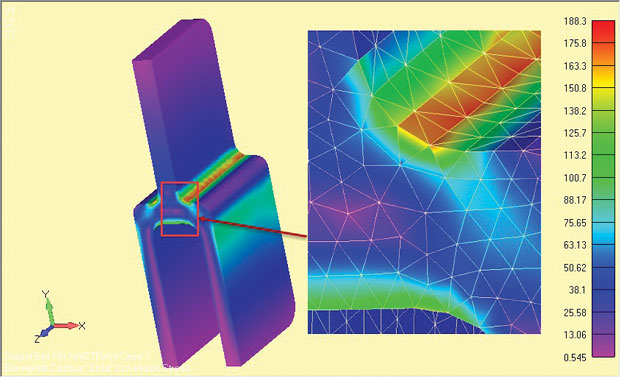Fig. 9: Volledig 3D-model van de diepe tang, die stressresultaten toont.

de plaatselijke schouderspanningen zijn in het volledige model een klein percentage lager. Dit is om drie redenen. Ten eerste is het relatief Grove 3D Tet mesh inferieur aan het zeer fijne 2D plane strain local mesh. Er is geen convergentiecontrole van het 3D-model uitgevoerd.

ten tweede is er een kleine verandering in de geometrie aan de vrije oppervlakken (+z, -z) ten opzichte van de sectie z = 0 als gevolg van de eindfilets. In dit geval is het effect verwaarloosbaar aangezien de filets uit de buurt van de schoudergebieden zijn. In veel componenten, echter, zullen er lokale filets, en run out details. die de geometrie zal variëren van een eenvoudige XY vlakke zijde. Lokale spanningsvariaties aan vrije uiteinden kunnen moeten worden geschat of gecontroleerd met een volledig 3D-model.

ten slotte geldt voor een eindige dieptecomponent de aanname van een vaste z-beperking bij +z, – z-secties niet. De Z-stress zal diffunderen tot nul op de” echte ” vrije gezichten. Dit effect wordt weergegeven in Fig. 10, die gebruik maakt van het 3D-model zoals het is en ook als een simulatie van de plane strain z stress.

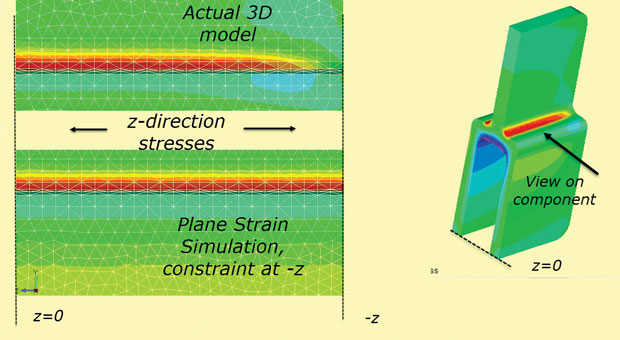Fig. 10: diffusie van z-stress naar het vrije oppervlak.

snelle en efficiënte

vlakke spannings-en spanningsanalyses zijn nuttige 2D-methoden die vaak full-scale 3D-modellen kunnen aanvullen. Niet alle functies kunnen worden weergegeven, maar met enige vindingrijkheid kunnen de spanningen op belangrijke gebieden op zijn minst worden geschat. De motivatie voor het gebruik van de methoden is om snelle en efficiënte analyse mogelijk te maken met eenvoudige 2D-geometrie en mesh-constructie.