Thermische geleidbaarheid

thermische geleidbaarheid van vaste stoffen is van een andere aard, afhankelijk van het feit of ze al dan niet geleiders. In diëlektrische systemen zonder vrije elektrische ladingen wordt thermische energie overgedragen door fononen. De collectieve trillingen van atomen in kristalrooster nemen de vorm aan van verplaatsingsgolven, waarvan de interferentie golfpakketten genereert, d.w.z. fononen. De verplaatsingsgolven veroorzaken schommelingen in dichtheid die zich kunnen manifesteren als een variatie van brekingsindex. Als de golven door een gebied gaan waarin de brekingsindex verschilt van de gemiddelde volumetrische waarde, zullen de daaropvolgende verplaatsingsgolven die de energie van thermische beweging dragen, worden verspreid.

de verstrooiing is sterker, hoe groter de maximale afwijking van atomen van hun gemiddelde posities in het rooster, d.w.z. hoe hoger de T. Dit verklaart het experimenteel vastgestelde feit dat de thermische geleidbaarheid van kristaldiëlektrie bij vrij hoge temperaturen afneemt: λ1/T (figuur 1).

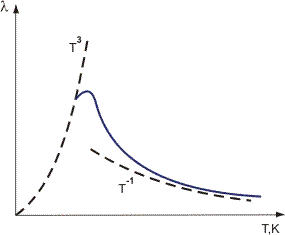
figuur 1. Variatie van thermische geleidbaarheid van kristal diëlektrics met temperatuur.

Debye gaf inzicht in een piekachtig karakter van λ(T) variatie bij lage T binnen het kader van kwantummechanische Concepten. Hij ontwikkelde een dipooltheorie gebaseerd op het concept van een molecuul als een stijve dipool. In dit model introduceerde Debye het concept van de zogenaamde Debye temperatuur θD proportioneel aan de maximale frequentie van atomaire trillingen in een vaste stof. Voor de meeste stoffen is θD lager dan of dicht bij de kamertemperatuur (een uitzondering is diamant waarvoor θD = 1850 K en berrylium waarvoor θD = 1160K).

in de kwantumtheorie van vaste stoffen wordt het kristalrooster beschouwd als een met fonongas gevuld volume waarop de deductie van de eenvoudigste kinetische theorie wordt toegepast.

waarbij c de warmtecapaciteit is van een diëlektricum dat samenvalt met die van fonongas, v De gemiddelde snelheid van fononen die ongeveer gelijk is aan de geluidssnelheid,het gemiddelde vrije pad van fononen. Het bestaan van een bepaalde eindige waarde vanis het resultaat van fononverstrooiing op fononen, op defecten van kristalrooster en, in het bijzonder, op korrelgrenzen over het gehele specimen. De temperatuurafhankelijkheid λ (T) wordt bepaald door die vanen c van de temperatuur.

bij hoge temperaturen die de Debye-temperatuur θD aanzienlijk overschrijden, is het basismechanisme datbegrenst een phonon-phononverstrooiing als gevolg van anharmoniciteit van atoomtrillingen in een kristal. Het phonon-phonon mechanisme van thermische weerstand ((1/λ) is bekend als de coëfficiënt van thermische weerstand) is alleen haalbaar als gevolg van een overgang die resulteert in vertraging van phonon flow en merkbare verandering van quasi-momentum. Hoe hoger de T, hoe hoger de kans op de overgang met afnemende:(1/T). Aangezien bij T > θD warmtecapaciteit c slechts licht toeneemt met de temperatuur, vandaar λ1 / T.

bij temperaturen die lager zijn dan de Debye-temperatuur, T<< θD, neemt de lengte van het gemiddelde vrije padbepaald door de phonon-phononverstrooiing drastisch toe,expθD/T en wordt in de regel beperkt tot de grootte van een kristal R. volgens de Debye-wet varieert de warmtecapaciteit c in dit temperatuurbereik als c(t/θD)3. Bijgevolg moet bij T → 0 de warmtegeleidingscoëfficiënt λ in verhouding tot T3 afnemen. De temperatuur waarvoor de warmtegeleiding een piek heeft, wordt bepaald van ≈ R, wat gewoonlijk overeenkomt met T ≤ 0,05 θD.

deze theorie houdt ook rekening met het gedrag van de warmtegeleidingscoëfficiënt voor amorfe stoffen zonder langeafstandsorde, d.w.z. de grootte van hun “kristallen” is van de Orde van atomaire grootte. Op grond hiervan moet de verstrooiing aan de “grenzen” van deze stoffen prevaleren bij alle T en≈ const. De warmtegeleidingscoëfficiënt van amorfe stoffen λT3 bij lage temperaturen en moet licht toenemen, in verhouding tot de warmtecapaciteit, bij matige en hoge temperaturen, t > θD.

dit alles geeft een kwalitatieve verklaring voor de afhankelijkheid λ(T) in reële kristaldiëlektrie, maar houdt geen rekening met afwijkingen van het constante rooster als gevolg van atomaire onzuiverheden van andere elementen en hun eigen isotopen. Bij een hoge temperatuur is de weerstand die wordt aangeboden door onzuiverheden om het transport te verwarmen onafhankelijk van de temperatuur. Dit maakt het mogelijk om de mate van kristalzuiverheid te schatten uit variatie van de thermische geleidbaarheid met temperatuur. Hetzelfde feit stelt ons in staat om de verdeling tussen glasachtige en kristalsubstantie in het natuurlijke mineraal te bepalen als het glas als een onzuiverheid in een kristal wordt beschouwd.

de thermische geleidbaarheid van metalen is afhankelijk van de beweging en interactie van stroomdragers, d.w.z. geleidingselektronen. In het algemeen is de warmtegeleidingscoëfficiënt λ van een metaal gelijk aan de som van rooster (fonon) λph, en elektron λe componenten, λ = λe + λph; bij gewone temperaturen, in de regel, λe >>λph.

als we een eenvoudige kinetische theorie van gassen toepassen op de stroom van vrije elektronen en aannemen dat de lengte van hun vrije pad niet afhangt van de snelheid, dan impliceert de theorie dat

waarbij e de elektronenlading is, de constante van K Boltzrnann en σ de elektrische geleidbaarheid. Een strikte kwantummechanische theorie biedt een soortgelijke relatie,

in beide formules blijkt de verhouding van het elektronendeel van de warmtegeleidingscoëfficiënt λ tot de elektrische geleidbaarheid σ, in een breed temperatuurbereik, in verhouding te zijn tot de temperatuur volgens de Wiedemann-Franz wet, λ / σ = LT, waarbij L Het Lorentzgetal is. Deze wet wordt gebruikt om λe uit de gemeten elektrische geleidbaarheid te berekenen. Echter, het wordt geschonden bij temperaturen onder θD wanneer een elektron-fonon interactie prevaleert (σ groeit met het verminderen van T als T−5, terwijl le iets meer varieert als T−2).

uit de experimentele bevindingen blijkt dat de thermische geleidbaarheid van metalen bij hoge temperaturen in de regel een iets afnemende functie van de temperatuur is. Maar er zijn veel uitzonderingen. Zo, thermische geleidbaarheid van ijzer sterk afneemt met de temperatuur, terwijl tantaal en niobium tonen een positieve temperatuurcoëfficiënt.

van belang zijn de pogingen om de warmtegeleidingscoëfficiënten voor verschillende stoffen voor een enkele karakteristieke temperatuur te vergelijken, bijvoorbeeld voor het smeltpunt Tm van vaste stoffen. Zo heeft de statistische verwerking van experimentele gegevens door Missenard aangetoond dat de thermische geleidbaarheid van metalen bij het smeltpunt λ(T = Tm) = λm in verhouding staat tot λen de thermische geleidbaarheid van diëlektrische kristallen bij T = Tm in verhouding is tot, waarbij m De molecuulmassa is, n het aantal atomen in de chemische formule, ρ de dichtheid en het smeltpunt Tm in Kelvin.

warmtetransport in halfgeleiders is complexer dan in diëlektrische en metalen omdat de fonon-en elektronencomponenten voor hen even essentieel zijn. Een andere reden voor de complexiteit is het aanzienlijke effect van onzuiverheden, bipolaire diffusie en andere weinig bestudeerde factoren op warmteoverdracht.

het effect van druk op de warmtegeleiding van vaste stoffen kan met een goede nauwkeurigheid als lineair worden aangenomen, λ Voor vele metalen die met p.

groeien voor het effect van poreusheid op de warmtegeleiding van vaste stoffen zie poreus Medium.