SSIM został po raz pierwszy wprowadzony w dokumencie IEEE 2004, Image Quality Assessment: From Error Visibility to Structural Similarity. Streszczenie dostarcza dobrej intuicji do idei proponowanego systemu,
obiektywne metody oceny percepcyjnej jakości obrazu tradycyjnie starały się kwantyfikować widoczność błędów (różnic) między zniekształconym obrazem a obrazem referencyjnym przy użyciu różnych znanych właściwości ludzkiego układu wzrokowego. Przy założeniu, że ludzka percepcja wzrokowa jest wysoce przystosowana do wydobywania informacji strukturalnych ze sceny, Wprowadzamy alternatywne uzupełniające ramy oceny jakości oparte na degradacji informacji strukturalnych.
podsumowanie: autorzy przedstawiają 2 istotne punkty,
- większość technik oceny jakości obrazu polega na ilościowym określaniu błędów między obrazem referencyjnym a przykładowym. Wspólną metryką jest kwantyfikacja różnicy w wartościach każdego z odpowiadających pikseli między próbką a obrazami referencyjnymi (za pomocą, na przykład, błędu średniego kwadratu).
- ludzki system percepcji wzrokowej jest w stanie zidentyfikować informacje strukturalne ze sceny, a tym samym zidentyfikować różnice między informacjami uzyskanymi ze sceny referencyjnej i przykładowej. W związku z tym metryka, która replikuje to zachowanie, będzie działać lepiej w zadaniach, które wymagają rozróżnienia między próbką a obrazem referencyjnym.
metryka strukturalnego wskaźnika podobieństwa (SSIM) wyodrębnia 3 Kluczowe cechy z obrazu:
- Luminancja
- kontrast
- struktura
porównanie obu obrazów odbywa się na podstawie tych 3 CECH.
rys 1 podany poniżej pokazuje rozmieszczenie i przepływ systemu pomiaru podobieństwa strukturalnego. Sygnał X i sygnał Y odnoszą się do obrazów referencyjnych i przykładowych.

ale co oblicza ta metryka?
ten system oblicza współczynnik podobieństwa strukturalnego pomiędzy 2 podanymi obrazami, który jest wartością między -1 a +1. Wartość +1 oznacza, że 2 podane obrazy są bardzo podobne lub takie same, podczas gdy wartość -1 oznacza, że 2 podane obrazy są bardzo różne. Często wartości te są dostosowywane tak, aby znajdowały się w zakresie , w którym skraje mają to samo znaczenie.
teraz przyjrzyjmy się pokrótce, jak te funkcje są reprezentowane matematycznie i jak przyczyniają się do ostatecznego wyniku SSIM.
- Luminancja: Luminancja jest mierzona przez uśrednianie wszystkich wartości pikseli. Jest oznaczana przez μ (Mu), a wzór podany jest poniżej,
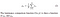
- Kontrast: Mierzy się ją, przyjmując odchylenie standardowe (pierwiastek kwadratowy wariancji) wszystkich wartości pikseli. Jest oznaczana przez σ (sigma) i reprezentowana przez poniższy wzór,
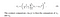
- Struktura: Porównanie strukturalne odbywa się za pomocą wzoru skonsolidowanego (więcej o tym później), ale w istocie dzielimy sygnał wejściowy z jego odchyleniem standardowym, tak aby wynik miał odchylenie standardowe jednostki, co pozwala na bardziej solidne porównanie.
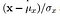
więc teraz ustaliliśmy matematyczną intuicję stojącą za trzema parametrami. Ale trzymaj się! Jeszcze nie skończyliśmy matematyki, trochę więcej. Brakuje nam teraz funkcji porównawczych, które mogą porównywać dwa podane obrazy na tych parametrach, a wreszcie funkcji kombinacji, która łączy je wszystkie. Tutaj definiujemy funkcje porównawcze i wreszcie funkcję kombinacyjną, która daje wartość indeksu podobieństwa
- funkcja porównania luminancji: jest zdefiniowana przez funkcję, l(x, y), która jest pokazana poniżej. μ (mu) oznacza średnią danego obrazu. x i y to dwa porównywane obrazy.
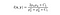
gdzie C1 jest stałą zapewniającą stabilność, gdy mianownik staje się 0. C1 otrzymuje się przez,
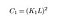
aktualizacja: w całym artykule nie zbadaliśmy, jakie są stałe K I L w tym równaniu. Na szczęście Czytelnik zwrócił na to uwagę w komentarzach, a więc w interesie uczynienia tego artykułu nieco bardziej pomocnym, zdefiniuję je tutaj.
L to zakres dynamiki wartości pikseli (ustawiamy go jako 255, ponieważ mamy do czynienia ze standardowymi obrazami 8-bitowymi). Możesz przeczytać więcej o tym, jakie są różne typy obrazów i co one oznaczają, tutaj.
K1, K2 to po prostu normalne stałe, nic tam nie ma!
- funkcja porównywania kontrastu: jest zdefiniowana przez funkcję c(x, y), która jest pokazana poniżej. σ oznacza odchylenie standardowe danego obrazu. x i y to dwa porównywane obrazy.
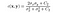
gdzie C2 jest podane przez,
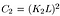
- funkcja porównywania struktury: jest zdefiniowana przez funkcję s(x, y), która jest pokazana poniżej. σ oznacza odchylenie standardowe danego obrazu. x i y to dwa porównywane obrazy.
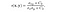
gdzie σ (xy) definiuje się jako,
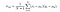
i na koniec wynik SSIM jest podany przez,

gdzie α > 0, β > 0, γ > 0 oznaczają względne znaczenie każdej z metryk. Aby uprościć wyrażenie, jeśli założymy, że α = β = γ = 1 i C3 = C2 / 2, możemy otrzymać,
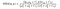
ale jest zwrot akcji!
chociaż można by zaimplementować SSIM przy użyciu powyższych formuł, są szanse, że nie będzie on tak dobry, jak dostępne gotowe do użycia implementacje, ponieważ autorzy wyjaśniają, że,
do oceny jakości obrazu przydatne jest stosowanie indeksu SSIM lokalnie, a nie globalnie. Po pierwsze, cechy statystyczne obrazu są zwykle bardzo przestrzennie niestacjonarne. Po drugie, zniekształcenia obrazu, które mogą, ale nie muszą, zależeć od lokalnych statystyk obrazu, mogą również być wariantem przestrzennym. Po trzecie, przy typowych odległościach widzenia tylko lokalny obszar obrazu może być postrzegany z wysoką rozdzielczością przez ludzkiego obserwatora w jednym momencie (ze względu na funkcję foveation HVS ). I wreszcie, lokalny pomiar jakości może zapewnić przestrzennie zmieniającą się mapę jakości obrazu, która dostarcza więcej informacji na temat degradacji jakości obrazu i może być przydatna w niektórych aplikacjach.
podsumowanie: Zamiast stosować powyższe metryki globalnie (tj. na całym obrazie jednocześnie), lepiej zastosować metryki regionalnie (tj. w małych fragmentach obrazu i biorąc średnią ogólną).
metoda ta jest często określana jako wskaźnik średniego podobieństwa strukturalnego.
ze względu na tę zmianę podejścia, nasze formuły również zasługują na modyfikacje odzwierciedlające to samo (należy zauważyć, że takie podejście jest bardziej powszechne i będzie używane do wyjaśnienia kodu).
(Uwaga: Jeśli treść poniżej wydaje się nieco przytłaczająca, nie martw się! Jeśli zrozumiesz sedno tego, przejrzenie kodu da ci o wiele jaśniejsze pojęcie.)
autorzy używają kołowo-symetrycznej funkcji ważenia Gaussa 11×11 (zasadniczo macierz 11×11, której wartości pochodzą z rozkładu Gaussa), która porusza się piksel po pikselu po całym obrazie. Na każdym kroku statystyki lokalne i indeks SSIM są obliczane w oknie lokalnym. Ponieważ obecnie obliczamy metryki lokalnie, nasze formuły są zmieniane jako,
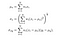
gdzie wi jest funkcją ważenia Gaussa.
jeśli uważasz, że to trochę nieintuicyjne, nie martw się! Wystarczy wyobrazić sobie Wi jako mnożeniei, które jest używane do obliczania wymaganych wartości za pomocą niektórych sztuczek matematycznych.
po wykonaniu obliczeń na całym obrazie, po prostu bierzemy średnią ze wszystkich lokalnych wartości SSIM i otrzymujemy globalną wartość SSIM.
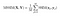
koniec z teorią! Przejdźmy do kodu!