Chciwy algorytm z przykładami: chciwa metoda i podejście

aby zrozumieć chciwe podejście, musisz mieć praktyczną wiedzę na temat rekurencji i przełączania kontekstu. Pomaga to zrozumieć, jak śledzić kod. Możesz zdefiniować chciwy paradygmat w kategoriach własnych niezbędnych i wystarczających stwierdzeń.

dwa warunki definiują chciwy paradygmat.

• każde krokowe rozwiązanie musi uporządkować problem w kierunku najlepszego zaakceptowanego rozwiązania.
• wystarczy, że ustrukturyzowanie problemu może zatrzymać się w skończonej liczbie chciwych kroków.

przy ciągłym teoretyzowaniu opiszmy historię związaną z zachłannym podejściem do poszukiwań.

w tym tutorialu chciwy algorytm, dowiesz się:

• Historia chciwych algorytmów
• chciwe strategie i decyzje
• charakterystyka chciwego podejścia
• dlaczego warto korzystać z chciwego podejścia?
• jak rozwiązać problem wyboru aktywności
• Architektura chciwego podejścia
• wady chciwych algorytmów

Historia chciwych algorytmów

oto ważny punkt orientacyjny chciwych algorytmów:

• algorytmy chciwości były konceptualizowane dla wielu algorytmów chodzenia po grafie w latach 50.
• Esdger Djikstra konceptualizował algorytm generowania minimalnych drzew rozpiętości. Jego celem było skrócenie rozpiętości tras w stolicy Holandii, Amsterdamie.
• w tym samym dziesięcioleciu Prim i Kruskal osiągnęły strategie optymalizacji, które opierały się na minimalizacji kosztów tras wzdłuż ważonych tras.
• w latach 70. amerykańscy badacze, Cormen, Rivest i Stein zaproponowali rekurencyjną substrukturę chciwych rozwiązań w swojej książce classical introduction to algorithms.
• paradygmat chciwego wyszukiwania został zarejestrowany jako inny rodzaj strategii optymalizacji w rejestrach NIST w 2005 roku.
• do tej pory protokoły uruchamiające sieć, takie jak open-shortest-path-first (OSPF) i wiele innych protokołów przełączania pakietów sieciowych używają chciwej strategii, aby zminimalizować czas spędzony w sieci.

chciwe strategie i decyzje

logika w najprostszej formie sprowadzała się do „chciwości” lub „nie chciwości”. Stwierdzenia te zostały zdefiniowane przez podejście podjęte w celu postępu na każdym etapie algorytmu.

na przykład algorytm Djikstry wykorzystał stopniową zachłanną strategię identyfikującą hosty w Internecie poprzez obliczenie funkcji kosztowej. Wartość zwracana przez funkcję kosztu określa, czy następna ścieżka jest „chciwa”, czy”nie chciwa”.

krótko mówiąc, algorytm przestaje być chciwy, jeśli na jakimkolwiek etapie wykonuje krok, który nie jest lokalnie chciwy. Chciwe problemy ustają bez dalszego zakresu chciwości.

cechy chciwego podejścia

ważnymi cechami algorytmu metody chciwej są:

• istnieje uporządkowana lista zasobów, z przypisaniem kosztów lub wartości. Te ilościowo określają ograniczenia systemu.
• w czasie obowiązywania ograniczenia pobierana jest maksymalna ilość zasobów.
• na przykład w przypadku problemu planowania działań koszty zasobów są wyrażone w godzinach, a działania muszą być wykonywane w kolejności seryjnej.

po co stosować chciwe podejście?

oto powody stosowania chciwego podejścia:

• chciwe podejście ma kilka kompromisów, które mogą uczynić go odpowiednim do optymalizacji.
• jednym z głównych powodów jest natychmiastowe osiągnięcie najbardziej wykonalnego rozwiązania. W problemie wyboru aktywności (wyjaśnionym poniżej), jeśli przed zakończeniem bieżącej aktywności można wykonać więcej czynności, czynności te można wykonać w tym samym czasie.
• kolejnym powodem jest rekurencyjny podział problemu na podstawie warunku, bez potrzeby łączenia wszystkich rozwiązań.
• w problemie wyboru aktywności krok „rekurencyjny podział” jest osiągany przez skanowanie listy elementów tylko raz i rozważenie pewnych działań.

jak rozwiązać problem z wyborem aktywności

w przykładzie planowania aktywności jest czas „rozpoczęcia” i „zakończenia” dla każdej aktywności. Każda aktywność jest indeksowana przez numer w celach informacyjnych. Istnieją dwie kategorie aktywności.

1. rozważana aktywność: to aktywność, która jest odniesieniem, z którego analizowana jest zdolność do zrobienia więcej niż jednej pozostałej aktywności.
2. pozostałe działania: działania o co najmniej jednym wskaźniku poprzedzającym daną działalność.

całkowity czas trwania daje koszt wykonania czynności. To znaczy (finish – start) daje nam czas trwania jako koszt działania.

dowiesz się, że wielkość jest liczbą pozostałych czynności, które możesz wykonać w czasie rozważanej aktywności.

Architektura podejścia chciwego

Krok 1)

Skanuj listę kosztów aktywności, zaczynając od indeksu 0 jako rozważanego indeksu.

Krok 2)

gdy do tego czasu można zakończyć więcej działań, rozważana aktywność się kończy, rozpocznij wyszukiwanie jednej lub więcej pozostałych działań.

Krok 3)

jeśli nie ma już pozostałych działań, bieżąca pozostała aktywność staje się następną rozważaną aktywnością. Powtórz Krok 1 i krok 2, z nową rozważaną czynnością. Jeśli nie ma żadnych pozostałych działań, przejdź do kroku 4.

KROK 4)

zwróć związek rozważanych indeksów. Są to wskaźniki aktywności, które zostaną wykorzystane do maksymalizacji przepustowości.

Wyjaśnienie kodu

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

Wyjaśnienie kodu:

1. Dołączone pliki nagłówkowe / klasy
2. Maksymalna liczba działań dostarczonych przez użytkownika.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

Wyjaśnienie kodu:

1. przestrzeń nazw dla operacji strumieniowych.
2. definicja klasy dla czasu
3. znacznik czasu godziny.
4. domyślny konstruktor czasu
5. zmienna godzin.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

Wyjaśnienie kodu:

1. definicja klasy z aktywności
2. znaczników czasu definiująca czas trwania
3. wszystkie znaczniki czasu są inicjowane na 0 w domyślnym konstruktorze

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

Wyjaśnienie kodu:

1. Część 1 definicji klasy scheduler.
2. rozważany indeks jest punktem wyjścia do skanowania tablicy.
3. indeks inicjalizacji służy do przypisywania losowych znaczników czasu.
4. tablica obiektów activity jest dynamicznie przydzielana przy użyciu nowego operatora.
5. zaplanowany wskaźnik określa bieżącą lokalizację bazową chciwości.

Scheduler(){ considered_index = 0; scheduled = NULL;......

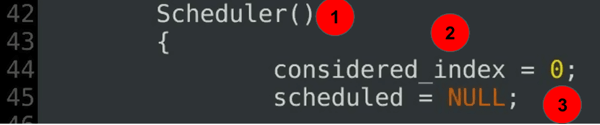
Wyjaśnienie kodu:

1. konstruktor schedulera-część 2 definicji klasy schedulera.
2. rozważany indeks określa bieżący początek bieżącego skanowania.
3. aktualny zakres jest nieokreślony na początku.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

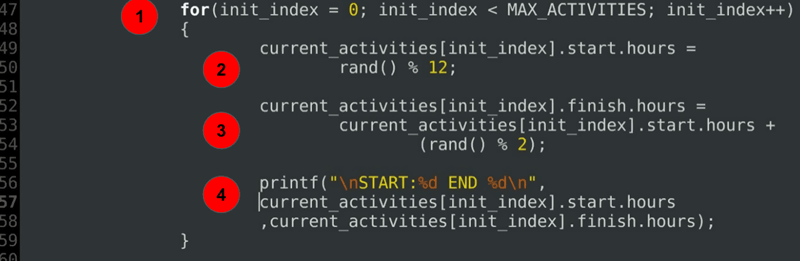
Wyjaśnienie kodu:

1. pętla for do inicjowania godzin rozpoczęcia i zakończenia każdej z aktualnie zaplanowanych czynności.
2. inicjalizacja czasu rozpoczęcia.
3. inicjalizacja czasu zakończenia zawsze po lub dokładnie w godzinie rozpoczęcia.
4. Instrukcja debugowania do drukowania przydzielonych czasów trwania.

public: Activity * activity_select(int);};

Wyjaśnienie kodu:

1. Część 4-Ostatnia część definicji klasy scheduler.
2. funkcja activity select przyjmuje indeks punktu początkowego jako bazę i dzieli chciwe zadanie na chciwe podproblemy.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. korzystając z operatora rozdzielczości zakresu (::), dostarczana jest definicja funkcji.
2. rozważanym indeksem jest indeks wywołany przez wartość. Greedy_extent jest inicjalizowanym tylko indeksem po rozważanym indeksie.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

Wyjaśnienie kodu:

1. logika rdzeń-chciwy zakres jest ograniczony do liczby działań.
2. godziny rozpoczęcia bieżącej aktywności są sprawdzane zgodnie z harmonogramem, zanim rozważana aktywność (podana przez rozważany indeks) zakończy się.
3. o ile to możliwe, drukowana jest opcjonalna Instrukcja debugowania.
4. przejdź do następnego indeksu w tablicy aktywności

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

Wyjaśnienie kodu:

1. warunkowe kontrole, czy wszystkie działania zostały objęte.
2. jeśli nie, możesz ponownie uruchomić chciwy z rozważanym indeksem jako bieżącym punktem. Jest to krok rekurencyjny, który chciwie dzieli stwierdzenie problemu.
3. jeśli tak, to wraca do rozmówcy bez możliwości rozszerzenia chciwości.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

Wyjaśnienie kodu:

1. główna funkcja używana do wywołania harmonogramu.
2. nowy harmonogram jest tworzony.
3. funkcja activity select, która zwraca wskaźnik typu activity wraca do wywołującego po zakończeniu chciwego zadania.

:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

wady chciwych algorytmów

Nie nadaje się do chciwych problemów, w których rozwiązanie jest wymagane dla każdego podproblemu, takiego jak sortowanie.

w takich zachłannych problemach z praktyką algorytmu, zachłanna metoda może być błędna; w najgorszym przypadku nawet prowadzić do nieoptymalnego rozwiązania.

dlatego wadą chciwych algorytmów jest używanie niewiedzy, co jest przed obecnym chciwym stanem.

poniżej przedstawiamy wadę metody zachłannej:

w skanie chciwości pokazanym tutaj jako drzewo (wyższa wartość wyższa chciwość), stan algorytmu przy wartości: 40 prawdopodobnie przyjmie 29 jako następną wartość. Co więcej, jego zadanie kończy się na 12. Wartość ta wynosi 41.

jednak, jeśli algorytm obrał nieoptymalną ścieżkę lub przyjął strategię podboju. następnie po 25 nastąpi 40, a ogólna poprawa kosztów wyniesie 65, co jest wyceniane o 24 punkty wyżej jako nieoptymalna decyzja.

przykłady chciwych algorytmów

większość algorytmów sieciowych używa podejścia chciwego. Oto lista kilku przykładów algorytmów chciwych:

• algorytm minimalnego drzewa rozpiętości Prima
• Problem podróżującego sprzedawcy
• kolorowanie wykresu na mapie
• algorytm minimalnego drzewa rozpiętości Kruskala
• algorytm minimalnego drzewa rozpiętości Dijkstry
• pokrywa wierzchołka wykresu
• problem z plecakiem
• problem z harmonogramem Zadań

podsumowanie:

Podsumowując, w artykule zdefiniowano chciwy paradygmat, pokazano, jak chciwa Optymalizacja i Rekursja mogą pomóc w uzyskaniu najlepszego rozwiązania do pewnego momentu. Chciwy algorytm jest szeroko stosowany do rozwiązywania problemów w wielu językach, takich jak chciwy algorytm Python, C, C#, PHP, Java itp. Wybór aktywności na przykładzie algorytmu chciwego został opisany jako problem strategiczny, który może osiągnąć maksymalną przepustowość przy użyciu podejścia chciwego. Ostatecznie wyjaśniono wady stosowania podejścia chciwego.