transformacja domowników
transformacja domowników (także „odbicie domowników”) jest ortogonalną transformacją odbicia:
- odwzorowuje wektory w kolumnach macierzy tak, że
- pierwszy wektor ma wszystkie zera z wyjątkiem pierwszego elementu
macierz transformacji
transformacja odbicia:
Nieruchomości
macierze są symetryczne i ortogonalne: są to matryce odbiciowe
Derywacja
więc mamy $p = I-2vv^t$:
używamy takich przekształceń do zerowania elementów
dekompozycja QR
podobnie jak w przypadku dekompozycji LU, gdzie zastosowaliśmy szereg zmian transformacji Gaussa, możemy zrobić to samo i wykonać serię przekształceń Housera
- więc jeśli wybierzemy $y = \pm e_1$ (gdzie $e_1$ to macierz z 1 na pozycji 1, a reszta to zera)
- to zeruje wszystkie elementy $x$ z wyjątkiem pierwszego
- Tak więc poprzez odpowiedni wybór $H$ możemy wziąć $a$ i zerować wszystkie przekątne elementy
- mogą to zrobić wiele razy dla każdej kolumny $A$
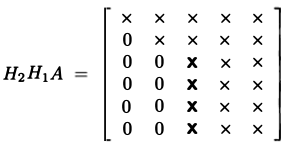
w ten sposób możemy wykonać dekompozycję QR:
rozkład Hessenberga
zamiast używać go do redukcji macierzy do trójkąta, możemy użyć przekształcenia Hessenberga do redukcji macierzy do macierzy Hessenberga