Householder Transformation
Householder Transformation (de asemenea, „Householder Reflection”) este o transformare de reflecție ortogonală:
- reflex vectorii din coloanele matricei astfel încât
- primul vector are toate zerourile, cu excepția primului element
matricea de transformare
transformare de reflecție:
proprietăți
matricile Householder sunt simetrice și ortogonale: sunt matrice de reflecție
derivare
deci avem $P = I – 2VV^t$:
folosim astfel de transformări pentru reducerea la zero a elementelor
descompunerea QR
ca și în cazul descompunerii LU, unde am aplicat o serie de schimbări de transformare Gauss, putem face același lucru și putem efectua o serie de transformări ale gospodăriei
- deci, dacă selectăm $y = \pm e_1$ (unde $e_1$ este matricea cu 1 pe poziția 1 și restul sunt zerouri)
- atunci va zero toate elementele de $x$, cu excepția 381>
- astfel, prin alegerea corespunzătoare a $h$ putem lua $a$ și zero toate sub-diagonale elemente
- pot face asta de mai multe ori pentru fiecare coloană de $a$
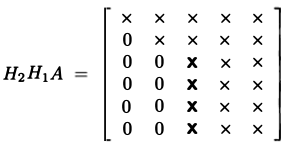
în acest fel putem efectua descompunerea QR:
descompunerea Hessenberg
în loc să o folosim pentru reducerea matricei la triunghiulară, putem folosi transformarea gospodăriei pentru a reduce o matrice la matricea Hessenberg